本文主要是介绍GPR 子波 一阶微分高斯脉冲和Ricker子波,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
gprMAX仿真时 用ricker子波,被审稿人咨询为什么用ricker波?
咨询了GPR设计专家,地耦雷达会用一阶高斯微分,空藕用ricker子波。实际上,我们都么有考虑这个。
给出matlab绘制代码
1 高斯脉冲
1.1 代码
% Parameters
amplitude = 1; % Amplitude of the pulses
pulse_width = 0.1; % Width of the pulses
center = 0; % Center position of the pulses
sampling_rate = 1000; % Number of samples per unit time% Time axis
t = -2:1/sampling_rate:2;% Gaussian pulse definition
gaussian_pulse = amplitude * exp(-((t-center)/pulse_width).^2);% First-order Gaussian differential pulse definition
gaussian_diff_1 = 2 * (t-center) .* gaussian_pulse / pulse_width^2;% Second-order Gaussian differential pulse definition
gaussian_diff_2 = 2 * ((t-center).^2 / pulse_width^2 - 1) .* gaussian_pulse / pulse_width^2;% Plotting the pulses
figure
subplot(3,1,1)
plot(t, gaussian_pulse);
xlabel('Time');
ylabel('Amplitude');
title('Gaussian Pulse');
xlim([-1 1])
subplot(3,1,2)
plot(t, gaussian_diff_1);
xlabel('Time');
ylabel('Amplitude');
title('First-Order Gaussian Differential Pulse');
xlim([-1 1])
subplot(3,1,3)
plot(t, gaussian_diff_2);
xlabel('Time');
ylabel('Amplitude');
title('Second-Order Gaussian Differential Pulse');
xlim([-1 1])1.2 结果
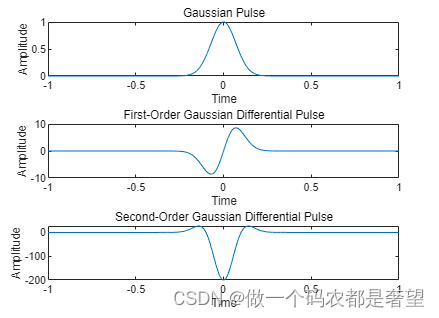
2 Ricker子波
2.1 代码
% Parameters
amplitude = 1; % Amplitude of the wavelet
frequency = 10; % Frequency of the wavelet
time_duration = 0.2; % Duration of the wavelet
time_offset = 0; % Time offset of the wavelet
sampling_rate = 1000; % Number of samples per unit time% Time axis
t = -2:1/sampling_rate:2;% Ricker wavelet definition
ricker_wavelet = amplitude * (1 - 2*pi^2*(frequency*(t-time_offset)).^2) .* exp(-pi^2*(frequency*(t-time_offset)).^2);% Plotting the wavelet
figure
plot(t, ricker_wavelet);
xlabel('Time');
ylabel('Amplitude');
title('Ricker Wavelet');
xlim([-1 1])2.2 结果
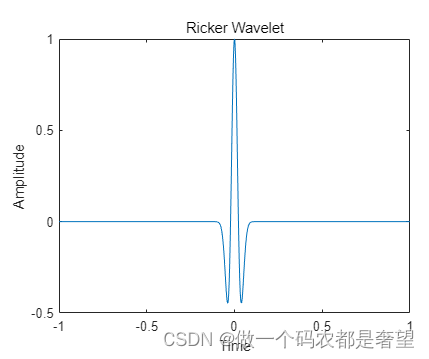
这篇关于GPR 子波 一阶微分高斯脉冲和Ricker子波的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







