Deep Reinforcement Learning for Automated Stock Trading An Ensemble Strategy

本文主要是介绍Deep Reinforcement Learning for Automated Stock Trading An Ensemble Strategy，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Deep Reinforcement Learning for Automated Stock Trading An Ensemble Strategy

论文

股票交易策略在投资中起着关键作用。然而，在复杂多变的股票市场上设计一个有利可图的策略是很有挑战性的。在本文中，我们提出了一种采用深度强化方案的集合策略，通过最大化投资收益来学习股票交易策略。我们训练了一个深度强化学习代理，并使用三种actor-critic based算法获得了一个集合交易策略。近端策略优化（PPO）、Advantage Actor Critic （A2C）和Deep Deterministic Policy Gradient（DDPG）。

集合策略继承并整合了三种算法的最佳特征，从而稳健地适应了不同的市场情况。为了避免在训练具有连续行动空间的网络时消耗大量内存，我们采用了按需加载技术来处理非常大的数据。我们在具有足够流动性的30只道琼斯股票上测试我们的算法。

对采用不同强化学习算法的交易代理的性能进行了评估，并与道琼斯工业平均指数和传统的最小方差投资组合分配策略进行了比较。拟议的深度集合策略在以夏普比率衡量的风险调整后的回报方面优于三种单独算法和两种基线。

I. INTRODUCTION

获利的自动股票交易策略对投资公司和对冲基金至关重要。它被用于优化资本配置和最大化投资业绩，如预期收益。收益最大化可以基于对潜在收益和风险的估计。然而，对于分析师来说，在一个复杂而动态的股市中考虑所有相关因素是具有挑战性的。

现有的工程并不令人满意。使用两个步骤的传统方法在[4]中描述。首先，计算股票预期收益和股票价格的协方差矩阵。然后，通过在给定的风险比下使收益最大化或在预先指定的收益下使风险最小化，就可以获得最佳的投资组合配置策略。然而，这种方法实施起来很复杂，而且成本很高，因为投资组合经理可能想要在每个时间步骤中修改决策，并考虑其他因素，比如交易成本。股票交易的另一种方法是将其建模为马尔科夫决策过程（MDP），并使用动态编程来得出最佳策略[5], [6], [7], [8]。然而，由于处理股票市场时的状态空间较大，这种模型的可扩展性是有限的。

近年来，机器学习和深度学习算法被广泛应用于构建金融市场的预测和分类模型。基础数据(收益报告)和替代数据(市场新闻、学术图表数据、信用卡交易和GPS流量等)与机器学习算法结合，提取新的投资阿尔法或预测一个公司的未来业绩[9]，[10]，[11]，[12]。

因此，产生了一个预测性的阿尔法信号来进行选股。然而，这些方法只专注于挑选高业绩的股票，而不是在选定的股票之间分配交易头寸或股份。换句话说，机器学习模型没有被训练成头寸模型。

在本文中，我们提出了一种新颖的组合策略，结合三种深度强化学习算法，在复杂的动态股票市场中找到最佳交易策略。这三种行为批评算法[13]是Proximal Policy Optimization (PPO) [14], [15],Advantage Actor Critic (A2C) [16], [17], and Deep Deterministic Policy Gradient (DDPG) [18], [15], [19]。我们的深度强化学习方法在图1中描述。

在这里插入图片描述

通过应用集合策略，我们使交易策略更加稳健和可靠。我们的策略可以根据不同的市场情况进行调整，并在风险约束下实现收益最大化。首先，我们建立一个环境，定义行动空间、状态空间和奖励函数。第二，我们训练在环境中采取行动的三种算法。第三，我们使用衡量风险调整后收益的夏普比率将三种代理合在一起。合并策略的有效性通过其比最小方差组合配置策略和道琼斯工业平均指数1（DJIA）更高的夏普比率得到了验证。

本文的其余部分组织如下。第2节介绍了相关工作。第3节对我们的股票交易问题进行了描述。在第4节中，我们设置了我们的股票交易环境。在第5节中，我们驱动并指定了三种基于行为批判的算法和我们的组合策略。第6节描述了股票数据的预处理和我们的实验设置，并介绍了拟议的集合策略的性能评估。

II. RELATED WORKS

critic-only学习方法是最常见的，它使用例如深度Q-learning（DQN）及其改进来解决离散行动空间问题，并在单一股票或资产上训练agent[21], [22], [23]。 critic-only方法的想法是使用一个Q值函数来学习最佳行动选择策略，该策略在当前状态下使预期的未来奖励最大化。DQN不是计算状态-动作值表，而是最小化估计的Q值和目标Q值之间的误差，并使用神经网络来进行函数近似。critic-only方法的主要限制是它只适用于离散和有限的状态和行动空间，这对大型股票组合来说是不实际的，因为价格当然是连续的。

这里的想法是，代理人直接学习最优策略。与其让神经网络来学习Q值，不如让神经网络来学习策略。政策是一个概率分布，本质上是一个给定状态的策略，即采取允许行动的可能性。仅有行为者的方法可以处理连续的行动空间环境。
actor-critic方法最近被应用于金融领域[27], [28], [17], [19]。其思路是同时更新代表政策的actor网络和代表价值函数的critic网络。批评者估计价值函数，而actor在critic的指导下用政策梯度更新政策概率分布。随着时间的推移，actor学会了采取更好的行动，而critic在评估这些行动时也变得更好。事实证明，actor-critic的方法能够学习和适应大型复杂的环境，并被用来玩流行的视频游戏，如Doom[29]。因此， actor-critic的方法在大型股票组合的交易中很有前景。

III. PROBLEM DESCRIPTION

我们将股票交易建模为马尔科夫决策过程（MDP），并将我们的交易目标表述为预期收益最大化[30]。

A. MDP Model for Stock Trading

为了模拟动态股票市场的随机性，我们采用了如下的马尔可夫决策过程(MDP):

通过将几个增强链的结果以凸形组合的方式混合在一起，这种图像退化可以得到缓解，增强的多样性也可以得到保持。该算法的具体说明在下面的伪代码中给出。

状态s = [p, h, b]：一个向量，包括股票价格 $p∈R^D_+$ ，股票份额 $h∈Z^D_+$ ，以及剩余的余额 $b∈R_+$ ，其中D表示股票的数量，Z+表示非负整数。
action a：D个股票的action向量。每只股票允许的行动包括卖出、买入或持有，分别导致股票h的减少、增加和没有变化。
奖励 $r (s, a, s^{'})$ ：在状态s采取行动a并到达新状态 $s^{'}$ 的直接奖励。
策略π(s)：状态s下的交易策略，即状态s下行动的概率分布。
Q值 $Q_π(s, a)$ ：在状态s下按照策略π采取行动a的预期回报。

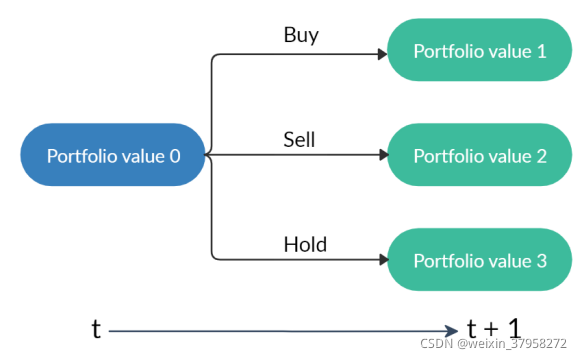
在这里插入图片描述

图2. 一个起始的投资组合值与三种行动会产生三种可能的投资组合。请注意，由于股票价格的变化，"持有 "可能导致不同的投资组合值。

股票交易过程的状态转换如图2所示。在每个状态下，对投资组合中的股票 $d (d = 1 ， . . . ， D)$ 采取三种可能行动之一。

出售 $k [d] \in [1, h [d]]$ 股份得到 $h_{t+1}[d] = h_t[d]−k[d]$ ，其中 $k[d]∈Z_+$ ， d = 1，…D。
持有， $h_{t+1}[d] = h_t[d]$
购买 $k [d]$ 股票导致 $h_{t+1}[d] = h_t[d] + k[d]$ 。

在时间t采取了行动，股票价格在t+1更新，相应地，投资组合价值可能从 "投资组合价值0 "分别变为 “投资组合价值1”、"投资组合价值2 "或 “投资组合价值3”，如图2所示。请注意，投资组合价值是 $p^Th + b$ 。

B. Incorporating Stock Trading Constraints

以下假设和约束反映了对实践的关注:交易成本、市场流动性、风险规避等。

市场流动性:可以在收盘时快速执行订单。我们假设股票市场不会受到我们的强化交易agent的影响。
非负余额b≥0：允许的行动不应导致负余额。根据时间t的行动，股票被分为卖出 $\mathcal S$ 、买入 $\mathcal B$ 和持有 $\mathcal H$ 的集合，其中 $\mathcal S∪\mathcal B∪\mathcal H=\{1, ..., D\}$ ，它们是不重叠的。让 $p^B_t = [p^i_t: i∈\mathcal B]和k^B_t = [k^i_t: i∈\mathcal B]$ 为买入集合中股票的价格和买入股数的向量。我们同样可以为卖出股票定义 $p^S_t和k^S_t$ ，为持有股票定义 $p^H_t和k^H_t$ 。因此，非负余额的约束条件可以表示为

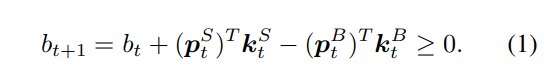
在这里插入图片描述

交易成本：每次交易都会产生交易成本。有许多类型的交易成本，如交易所费用、执行费用和SEC费用。不同的经纪商有不同的佣金费用。尽管有这些费用上的差异，我们假设我们的交易成本是每笔交易价值的0.1%（无论是买还是卖），如[9]。
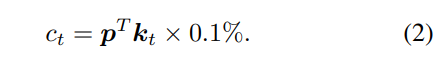
对市场崩溃的风险规避：有一些突发事件可能导致股票市场崩溃，如战争、股市泡沫崩溃、主权债务违约和金融危机。为了控制像2008年全球金融危机这种最坏情况下的风险，我们采用了衡量极端资产价格变动的金融动荡指数turbulencet[31]。

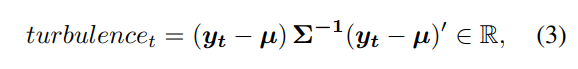
其中 $y_t∈R^D$ 表示当前时期t的股票收益， $μ∈R^D$ 表示历史收益的平均值， $Σ∈R^{D×D}$ 表示历史收益的协方差。当turbulencet高于阈值时，表示极端的市场状况，我们就会简单地停止购买，交易员会卖出所有的股票。一旦动荡指数回到阈值以下，我们就恢复交易。

C. Return Maximization as Trading Goal
我们将奖励函数定义为在状态s下采取行动a并到达新状态 $s^{'}$ 时的投资组合价值的变化。我们的目标是设计一个能使投资组合价值变化最大化的交易策略。
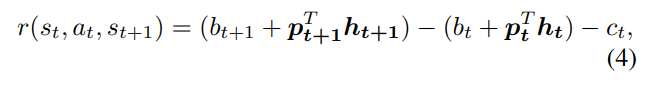
在这里插入图片描述
其中第一项和第二项分别表示t+1和t时的投资组合价值。为了进一步分解收益，我们将股票的过渡期 $h_t$ 定义为

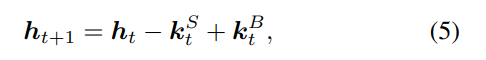
和余额 $b_t$ 的过渡在（1）中定义。那么 (4)可以改写为

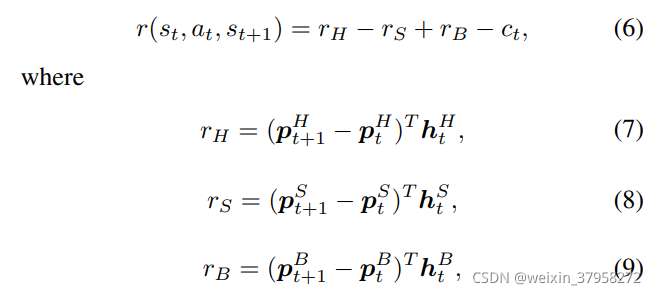
其中 $r_H、r_S和r_B$ 分别表示从时间t到t+1，持有、卖出和买入股票所带来的投资组合价值的变化。公式（6）表明，我们需要通过买入并持有在下一时间段价格会上涨的股票，使投资组合价值的正向变化最大化，通过卖出在下一时间段价格会下跌的股票，使投资组合价值的负向变化最小化。

Turbulence index $turbulence_t$ 与奖励函数结合在一起，以解决我们对市场崩溃的风险厌恶。当（3）中的指数超过一个阈值时，方程（8）变为
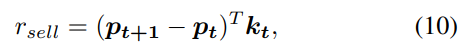
在这里插入图片描述
这表明我们希望通过卖出所有持有的股票来尽量减少投资组合价值的负面变化，因为所有的股票价格都会下跌。模型的初始化如下。 $p_0$ 被设定为时间0的股票价格， $b_0$ 是初始基金的数额。h和 $Q_π(s, a)$ 为0，π(s)在每个状态的所有行动中均匀分布。然后， $Q_π(s_t, a_t)$ 通过与股票市场环境的互动而被更新。最佳策略由贝尔曼方程给出，在状态 $s_t$ 采取行动的预期报酬是直接报酬r(st, at, st+1)和下一个状态 $s_{t+1}$ 的未来报酬之和的预期。为了收敛的目的，让未来的奖励被折现为0 < γ < 1的系数，那么我们有
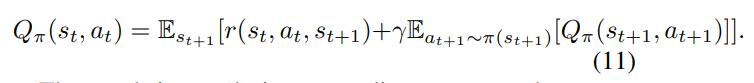
在这里插入图片描述
目标是设计一个交易策略，使投资组合价值 $r(s_t, a_t, s_{t+1})$ 在动态环境中的正向累积变化最大化，我们采用深度强化学习方法来解决这个问题。

IV. STOCK MARKET ENVIRONMENT

在训练深度强化交易代理之前，我们仔细搭建模拟真实世界的交易环境，让代理进行交互和学习。在实际交易中，需要考虑各种信息，例如历史股票价格，当前持有的股份，技术指标等。我们的贸易代理需要通过环境获取这些信息，并采取上一节定义的行动。我们使用OpenAI体育馆来实现我们的环境，训练代理[32]，[33]，[34]。

A. Environment for Multiple Stocks

我们使用一个连续动作空间来建模多只股票的交易。我们假设我们的投资组合总共有30只股票。

1)状态空间:我们使用由7部分信息组成的181维向量来表示多只股票交易环境的状态空间: [bt, pt, ht,Mt, Rt, Ct, Xt]。每个组件的定义如下:
在这里插入图片描述

$R_t∈R_{30}^+$ ：Relative Strength Index（RSI）是用收盘价计算的。使用收盘价。RSI量化了近期价格变化的程度。价格变化的程度。如果价格在支撑线附近移动。它表明该股票是超卖的，我们可以执行买入行动。如果价格在阻力线附近移动，它表明该股已经超买，我们可以执行卖出行动。[35].
$C_t∈R_{30}^+$ ：商品通道指数（CCI）是用最高价、最低价和收盘价计算的。CCI将当前价格与某一时间窗口的平均价格进行比较，以表明买入或卖出行动[36]。
$X_t∈R_{30}$ : 平均方向性指数（ADX）是使用最高价、最低价和收盘价计算。ADX 通过量化价格运动的数量来识别趋势强度。价格运动[37]。