每日一题 2316. 统计无向图中无法互相到达点对数（中等，图连通分量）

本文主要是介绍每日一题 2316. 统计无向图中无法互相到达点对数（中等，图连通分量），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

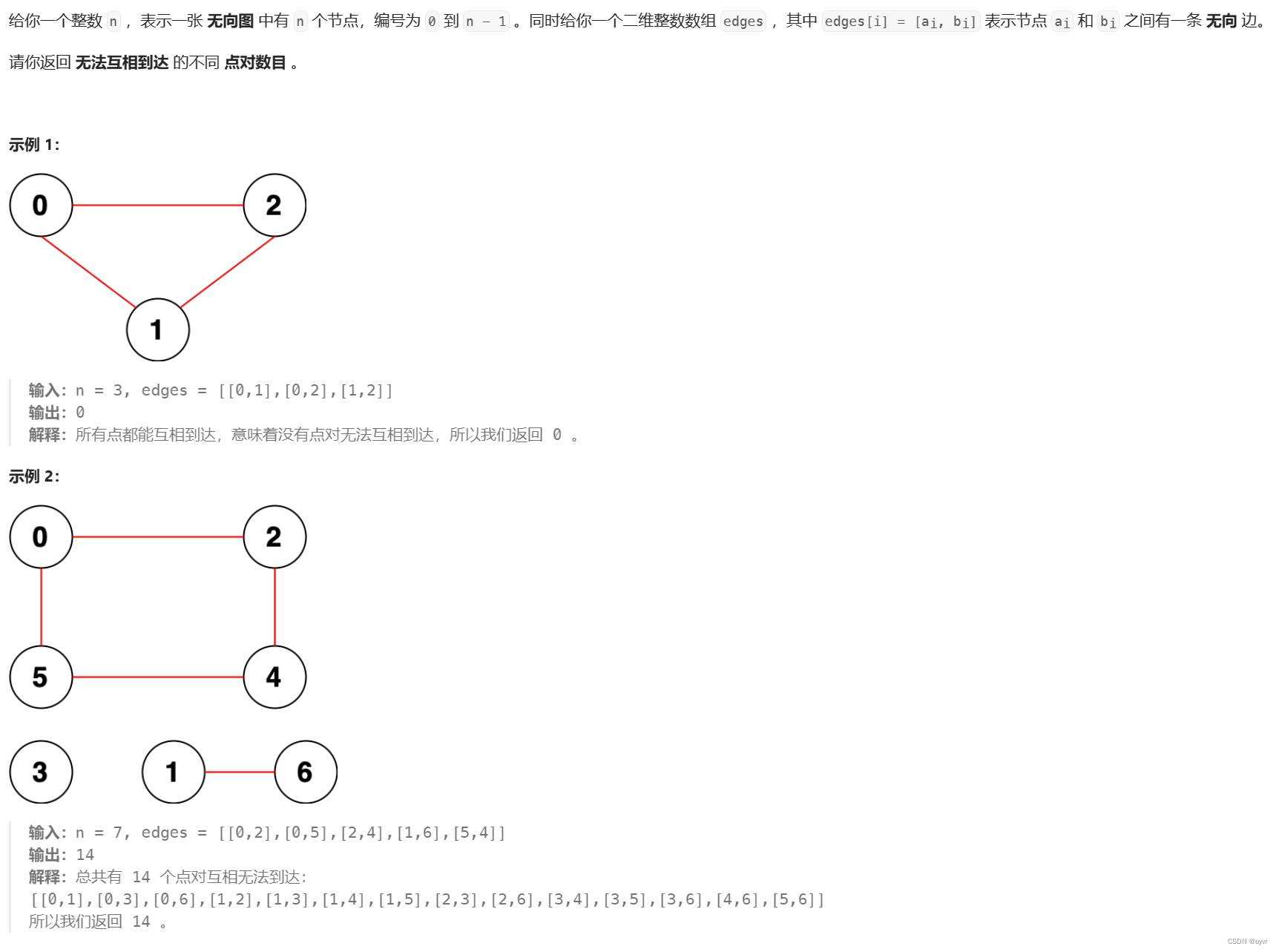
1. 题目很简单，只要求出每个连通分量有多少个节点即可
2. 首先通过建立一个字典来表示每个节点的邻接关系
3. 遍历每个节点，并通过邻接关系标记在当前连通分量内的所有的点，这样就可以知道一个连通分量内有多少个点
4. 在这里我陷入了一个误区，导致最后超时，我一开始把所有的连通分量的点数都求出来之后，再将他们两两组合得到最后的答案（耗时O(a²) 其中a是连通分量的数量），而事实上对于每个连通分量它的组合数就是 cnt * (n - cnt) 只要 O(a) 就可以求出来，最后由于每一个点对都被计算了两次，因此需要 ans // 2

class Solution:def countPairs(self, n: int, edges: List[List[int]]) -> int:d = defaultdict(list)isCnt = set()for i in range(len(edges)):d[edges[i][0]].append(edges[i][1])d[edges[i][1]].append(edges[i][0])ans = 0for i in range(n):if i in isCnt:continuecnt = 1l = d[i]isCnt.add(i)while len(l) > 0:newl = []for j in l:if j in isCnt:continuenewl.extend(d[j])cnt += 1isCnt.add(j)l = newl.copy()ans += cnt * (n - cnt)return ans // 2

这篇关于每日一题 2316. 统计无向图中无法互相到达点对数（中等，图连通分量）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---