本文主要是介绍李航《统计学习方法》第一天之过拟合与泛化误差,极大似然估计和贝叶斯估计,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
写在前面:《统计学习方法》各章节代码实现与课后习题参考解答 https://blog.csdn.net/breeze_blows/article/details/85469944
1.、过拟合
概念:过拟合简单的说来就是就是训练出来的模型在训练集上表现很好,但是在测试集上表现较差的一种现象!
模型出现过拟合现象的原因:
发生过拟合的主要原因可以有以下三点:
(1)数据有噪声
意思就是把一些干扰点给训练进去了,而且训练集上整个表现都很好,但是由于测试集里面不包含干扰点(即使包含了也是错的),导致测试输出也还是十分的差劲。引用两幅图可以更加直观。
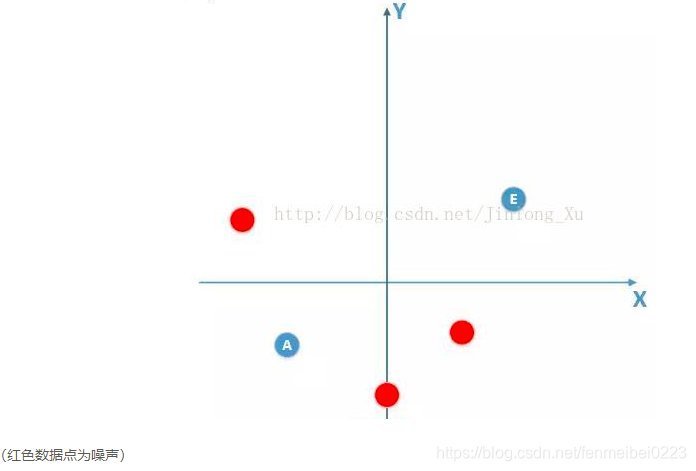
在经过一系列的训练之后,也许就会训练出下图的模型:
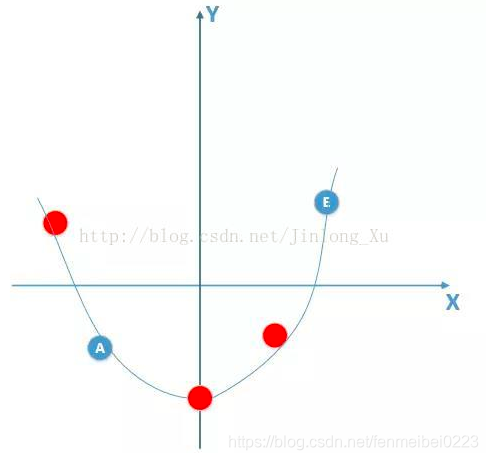
但是,这个是我们想要的吗?并不是!看似十分完美,损失函数为,但是拿到测试集里一检验就会出现很大的误差。
(2)训练数据不足,有限的训练数据
这个原因也十分的好理解,上图有4个点,假设4个点都是待训练集中的实际点,但是由于数据不足,我们可能只训练了左边的两个点,那这样得出来的模型会和实际的模型相差甚远。
(3)训练模型过度导致模型非常复杂
训练模型过度导致模型非常复杂,也会导致过拟合现象!这点和第一点俩点原因结合起来其实非常好理解,当我们在训练数据训练的时候,如果训练过度,导致完全拟合了训练数据的话,得到的模型不一定是可靠的。
比如说,在有噪声的训练数据中,我们要是训练过度,会让模型学习到噪声的特征,无疑是会造成在没有噪声的真实测试集上准确率下降!
2.泛化误差
我也不是很明白这个公式的推导过程。
3.极大似然估计
https://wenku.baidu.com/view/0d9af6aa172ded630b1cb69a.html 这一个链接里面的ppt说的还是很明白了。
4.贝叶斯估计:
https://blog.csdn.net/qq_32742009/article/details/81481680 看的懵懵懂懂,主要是不知道怎么运用。
最后,加上一个:
贝叶斯估计和极大似然估计到底有何区别 :https://blog.csdn.net/feilong_csdn/article/details/61633180
这篇关于李航《统计学习方法》第一天之过拟合与泛化误差,极大似然估计和贝叶斯估计的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



