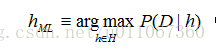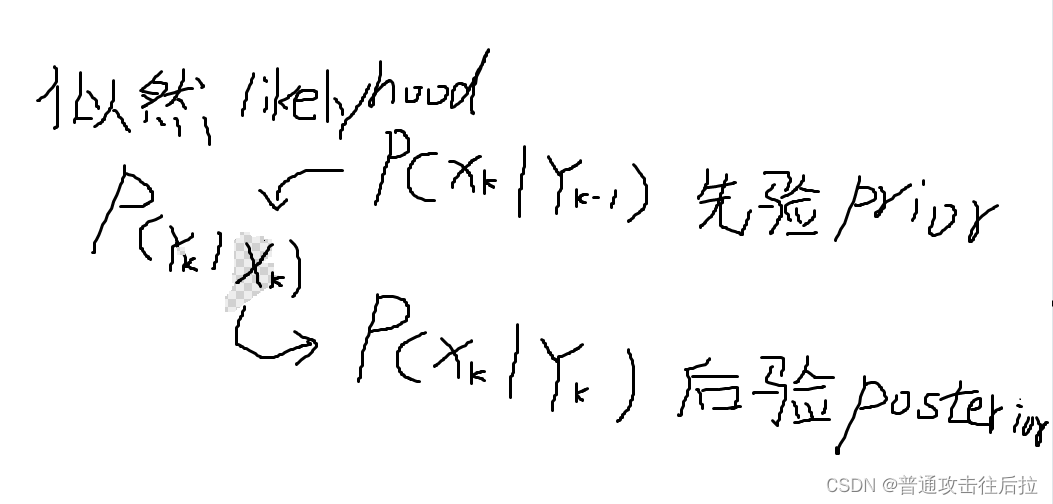极大专题

带小数点数值的极大次方求解

转自 http://blog.csdn.net/rually/article/details/8585268 http://poj.org/problem?id=1001 原题如下： Exponentiation Time Limit: 500MS Memory Limit: 10000KTotal Submissions: 113486 Accepted: 27528

机器学习案例｜使用机器学习轻松预测信用卡坏账风险，极大程度降低损失

01、案例说明对于模型的参数，除了使用系统的设定值之外，可以进行再进一步的优化而得到更好的结果。RM提供了几种参数优化的方法，能够让整体模型的效率提高。而其使用的概念，仍然是使用计算机强大的计算能力，对于不同的参数组合进行准确度评估，使用硬算的方式选出最优的参数。这个也是机器学习里面的另外一个特点与优势。本案例讨论的是：对于信用卡公司需要判断客户会不会变成坏账（Default），从而预先防

ArrayList正确的使用可以极大的提示添加效率

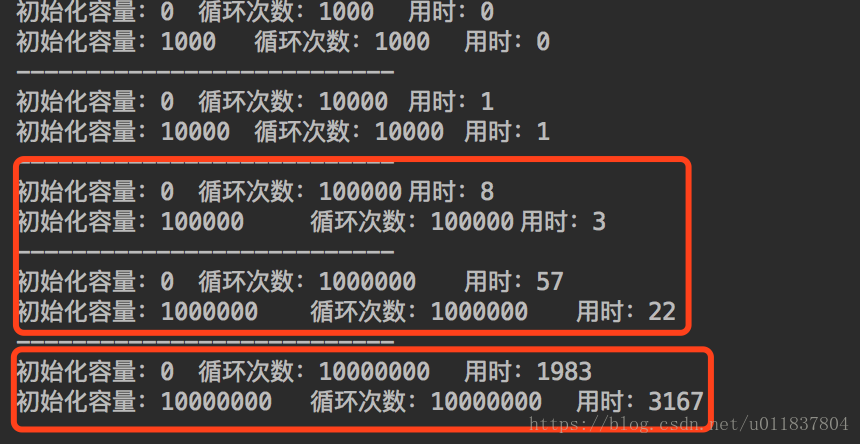
1、ArrayList原理 ArrayList底层使用可变长度数组存储元素在初始化ArrayList时，如果没有指定初始化容量或者指定0为初始化容量，那初始化容量将默认为10 在每次添加元素时，首先校验容量是否满足，如果不满足使用Arrays.copyOf方法，以原来容量的1.5倍扩容涉及到内存操作（创建新的数组，丢掉老的数组）导致效率比较低在每次删除元素时，使用Arrays.co

寻找平面上的极大点（信息学奥赛一本通-T1230）

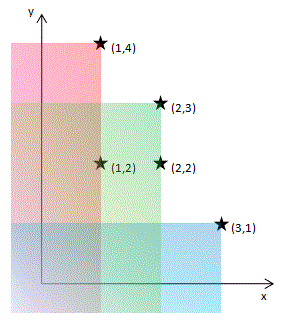
【题目描述】在一个平面上，如果有两个点(x,y),(a,b),如果说(x,y)支配了(a,b)，这是指x≥a,y≥b; 用图形来看就是(a,b)坐落在以(x,y)为右上角的一个无限的区域内。给定n个点的集合，一定存在若干个点，它们不会被集合中的任何一点所支配，这些点叫做极大值点。编程找出所有的极大点，按照x坐标由小到大，输出极大点的坐标。本题规定：n不超过100，并且不考虑点的坐标为负数

非极大抑制（Non-maximum suppression）

一、Nms主要目的在物体检测非极大抑制应用十分广泛，主要目的是为了消除多余的框，找到最佳的物体检测的位置。如上图中：虽然几个框都检测到了人脸，但是我不需要这么多的框，我需要找到一个最能表达人脸的框。下图汽车检测也是同样的原理。

贝叶斯学习--极大后验假设学习

我们假定学习器考虑的是定义在实例空间X上的有限的假设空间H，任务是学习某个目标概念c:X→{0,1}。如通常那样，假定给予学习器某训练样例序列〈〈x1，d1，〉…〈xm，dm〉〉，其中xi为X中的某实例，di为xi的目标函数值（即di=c(xi)）。为简化讨论，假定实例序列〈x1…xm〉是固定不变的，因此训练数据D可被简单地写作目标函数值序列：D=〈d1…dm〉。基于贝叶斯理论我们可以设计一

贝叶斯学习--极大后验概率假设和极大似然假设

在机器学习中，通常我们感兴趣的是在给定训练数据D时，确定假设空间H中的最佳假设。所谓最佳假设，一种办法是把它定义为在给定数据D以及H中不同假设的先验概率的有关知识条件下的最可能（most probable）假设。贝叶斯理论提供了计算这种可能性的一种直接的方法。更精确地讲，贝叶斯法则提供了一种计算假设概率的方法，它基于假设的先验概率、给定假设下观察到不同数据的概率、以及观察的数据本身。要

代码生成器，极大简化你的工作

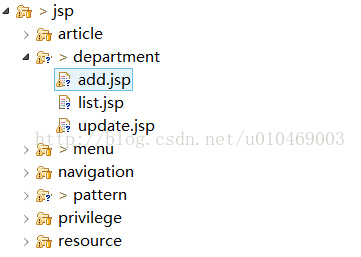
代码生成器，极大简化你的工作在web开发中，模块化开发非常普遍。在最近的毕业设计中，自己基于spring mvc + mybatics + liger ui开发了一个网站，里面也使用模块化来组织代码。于是每一个模块的操作，基本上都是大同小异，无非就是增删改查。下面先观察下代码的包组织结构，以及jsp文件组织结构：如下图所示。从图中可以看出

极大提高Web开发效率的8个工具和建议（含教程）

面对复杂的 Web 应用的开发，良好的流程和工具支持是必不可少的，它们可以让日常的开发工作更加顺畅、更加高效。本文介绍了6个Web开发利器以及相关的教程，帮助你在开发、调试、集成和发布过程极大地提高效率。 Sublime Text SublimeText 是一款非常精巧的文本编辑器，适合编写代码、做笔记、写文章。它用户界面十分整洁，功能非同凡响，性能快得出奇。这些非常棒的特性包括任意跳转（G

漫步最优化十一——局部极小与极大的充分必要条件(上)

即便没有那么多浪漫的话， \textbf{即便没有那么多浪漫的话，} 我也想与你走过每个冬夏。 \textbf{我也想与你走过每个冬夏。} 你的出现是我唯一的心动， \textbf{你的出现是我唯一的心动，} 你的与众不同让我难以忘记每个笑容。 \textbf{你的与众不同让我难以忘记每个笑容。} 越相处越习惯你， \textbf{越相处越习惯你，} 越想

杂记——极大似然估计的渐近正态性

结论假设 x 1 , ⋯ , x n x_1, \cdots, x_n x1,⋯,xn是来自 f θ ( x ) f_{\theta}(x) fθ(x)的独立同分布样本， θ ^ M L E \hat{\theta}_{MLE} θ^MLE是参数 θ \theta θ的极大似然估计，那么 θ ^ M L E ∼ ˙ N ( θ , 1 n I ( θ ) ) (1) \hat{\t

CSP认证 201803-4 棋局评估(极大极小值搜索)

题目链接：http://118.190.20.162/view.page?gpid=T70 题目大意：给一个3*3棋盘，问按照最优策略下，如果1能赢输出赢后剩余未下的格子数+1,2能赢输出赢后负的剩下未下的格子数-1，平局输出0 题目思路：3*3很小，直接暴力所有情况，先手下尽可能想让值高，反手下尽可能想让值低，所以只用在所有可能中尽可能取利于自己的情况即可以下是代码：

一文搞懂极大似然估计

极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。可能有小伙伴就要说了，还是有点抽象呀。我们这样想，一当模型满足某个分布，它的参数值我通过极大似然估计法求出来的话。比如正态分布中公式如下：如果我通过极大似然估计，得到模型

数据结构图中极大连通子图和极小连通子图的区别

极大连通子图要求该连通子图要包含其所有的边极小连通子图是在保持图连通的情况下，使得边数最少（即删除多余的边）极小连通子图可以看作在极大连通子图的基础上删除多余的边

StableDiffusion Web UI开启FP8，极大节约显存

升级了Pytorch后，StableDiffusion最新版本就可以有使用FP8的基础了，因此把秋叶的LINUX包也升级到了最新的版本。升级Pytorch参考我的升级记录： ComfyUI SDWebUI升级pytorch随记-CSDN博客然后下一步就是如何开启FP8了。与ComfyUI不同，SDWebUI不是通过启动参数来开启，而是在配置界面找到这个位置：记得点保存生效。

极大提高工作效率的 Linux 命令

作为一名软件开发人员，掌握 Linux 命令是必不可少的技能。即使你使用 Windows 或 macOS，你总会遇到需要使用 Linux 命令的场合。例如，大多数 Docker 镜像都基于 Linux 系统。要进行 DevOps 工作，你需要熟悉Linux，至少要了解一些常用命令。自定义bash提示符嗯，这个主题本身可以是一篇冗长的文章。不过，我们不需要学习所有的内容。在大多数情况下，我们

还在被机组组合问题困扰？快来试试这个用处极大的考虑安全约束机组组合模型！

前言所谓安全约束机组组合，即在满足电力系统安全性约束的条件下，以系统购电成本最低等为优化目标，制定多时段的机组开停机计划。机组组合(Unit commitment, Uc)优化问题旨在电力系统运行时，安全给定以及调整发电机组的启/停与实时出力，使发电机组的总运行成本最小。研究UC问题的混合整数规划方法，主要涉及机组组合模型紧且简洁的重构--紧性能减少求解器搜索空间，简洁性提高求解器搜索

基于极大极小算法和alpha-beta剪枝实现AI井字棋

关于极大极小算法和alpha-beta剪枝可以参考文章的参考资料，这里仅对其进行代码实现。其实这个算法单纯的理解并不容易，下面用代码进行实现。说一下实现这个AI井字棋的思路：简单的来说就是计算机希望估值函数值最大，而下棋人希望这个估值最小，因此在计算机决策是就用递归的向前看，这里的递归其实蛮不好理解的，但是可以宏观的去理解。下面是代码的构成：一个ChessBoard的类用来处

浅易理解：非极大抑制NMS

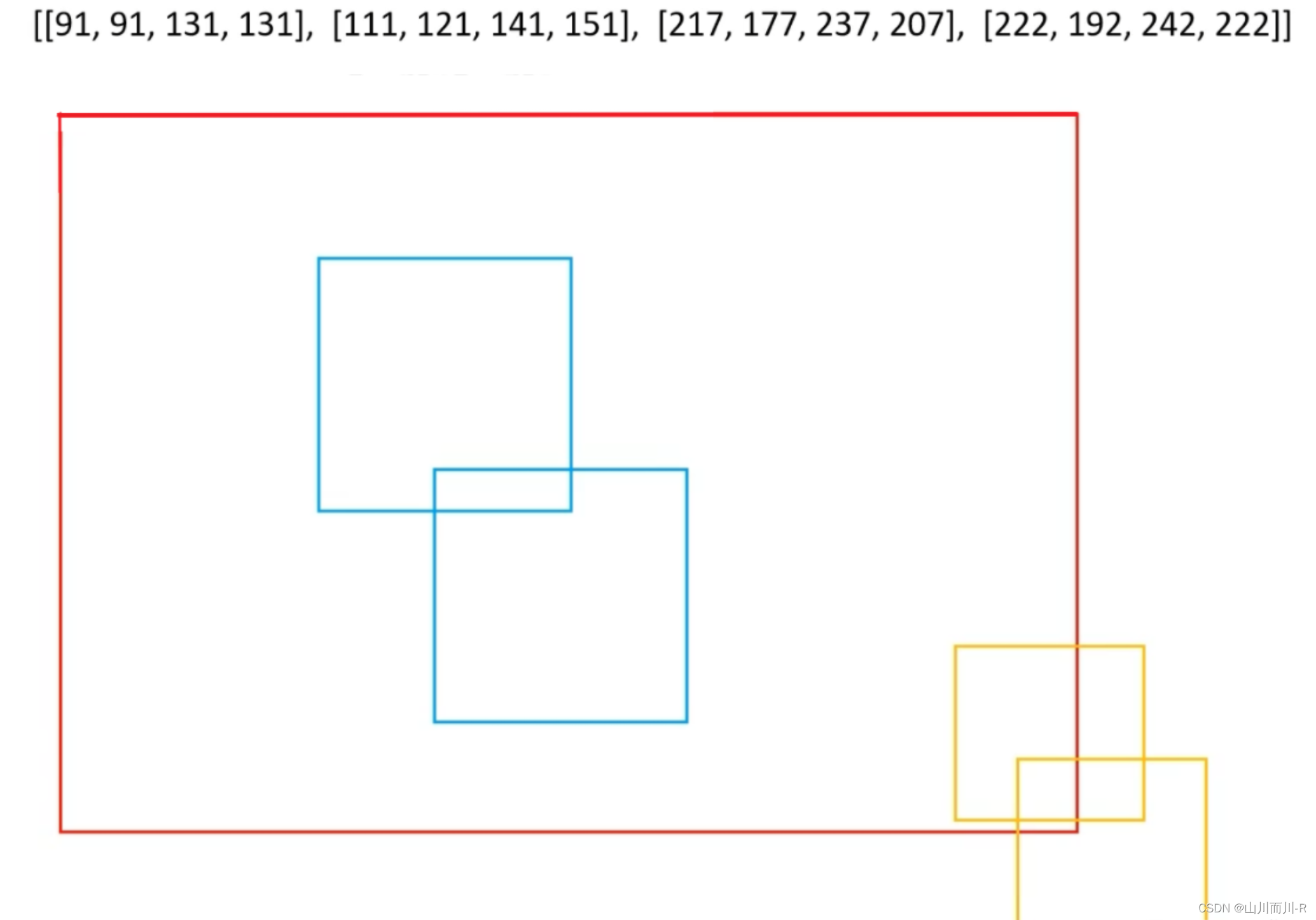
什么是非极大抑制NMS 非极大值抑制（Non-Maximum Suppression，简称NMS）是一种在计算机视觉和图像处理领域中广泛使用的后处理技术，特别是在目标检测任务中。它的主要目的是解决目标检测过程中出现的重复检测问题，即对于同一个物体，算法可能会预测出多个重叠或相似的边界框（bounding boxes）。在目标检测算法得出一系列候选边界框及其对应的类别得分（conf

先验分布、后验分布、极大似然的一点思考

今天和组里同事聊天的时候，无意中提到了贝叶斯统计里先验分布、后验分布、以及极大似然估计这三个概念。同事专门研究如何利用条件概率做系统辨识的，给我画了一幅图印象非常深刻：其中k表示时序关系。上面这个图表示后验分布是由先验分布与似然估计一同获得的。我们经常在代码里给神经网络的最后一层的各个unit的概率值叫likelyhood，其实就是指在当前输入样本下输出各个logit的概率，其含义与极大似

5. 数理统计---极大似然估计

这里写自定义目录标题 5.极大似然估计5.1 似然函数定义5.2 极大似然估计定义5.3 极大似然估计求解的一般过程5.4 极大似然估计的不变性 5.极大似然估计 Fisher的极大似然思想: 随机试验有多个可能结果, 但在一次实验中, 有且只有一个结果会出现. 如果在某次实验中, 结果 ω \omega ω出现了, 则认为该结果(事件{ ω \omega ω})发生的概率 P

基于极大似然算法的系统参数辨识matlab仿真

目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述基于极大似然算法的系统参数辨识。对系统的参数a1，b1，a2，b2分别进行估计，计算估计误差以及估计收敛曲线，然后对比不同信噪比下的估计误差。 2.测试软件版本以及运行结果展示 MATLAB2022a版本运行 3.核心程序

极大似然估计(MLE)和贝叶斯估计(MAP)

极大似然估计（MLE）和贝叶斯估计（MAP）标签（空格分隔）：机器学习笔记极大似然估计与贝叶斯估计是统计中两种对模型的参数确定的方法，两种参数估计方法使用不同的思想。前者来自于频率派，认为参数是固定的，我们要做的事情就是根据已经掌握的数据来估计这个参数（上帝眼中参数 θ \theta早已经固定了，带入 xi x_i样本来求 θ \theta，根据样本来求 θ \theta，最大的

概率基础——极大似然估计

概率基础——极大似然估计引言极大似然估计（Maximum Likelihood Estimation，简称MLE）是统计学中最常用的参数估计方法之一，它通过最大化样本的似然函数来估计参数值，以使得样本出现的概率最大化。极大似然估计在各个领域都有着广泛的应用，例如机器学习、生物统计学、金融等。本文将介绍极大似然估计的理论基础、公式推导过程，并通过案例和Python代码进行实现和模拟，以帮助读

Spark GraphX实现Bron–Kerbosch算法-极大团问题

首先，说明两个概念：团、极大团。团（clique）是一个无向图（undirected graph ）的子图，该子图中任意两个顶点之间均存在一条边。又叫做完全子图。极大团（maximal clique）是一个团，该团不能被更大的团所包含，换句话说，再也不存在一个点与该团中的任意顶点之间存在一条边。研究极大团的问题对社区发现等场景有较高的理论价值和现实意义。求一个无向图中的极大团问题是

【初中生讲机器学习】12. 似然函数和极大似然估计：原理、应用与代码实现

创建时间：2024-02-23 最后编辑时间：2024-02-24 作者：Geeker_LStar 你好呀~这里是 Geeker_LStar 的人工智能学习专栏，很高兴遇见你~ 我是 Geeker_LStar，一名初三学生，热爱计算机和数学，我们一起加油~！ ⭐(●’◡’●) ⭐ 那就让我们开始吧！在上一篇【初中生讲机器学习】11. 回归算法中常用的模型评价指标有哪些？here! 中