还在被机组组合问题困扰？快来试试这个用处极大的考虑安全约束机组组合模型！

本文主要是介绍还在被机组组合问题困扰？快来试试这个用处极大的考虑安全约束机组组合模型！，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

所谓安全约束机组组合，即在满足电力系统安全性约束的条件下，以系统购电成本最低等为优化目标，制定多时段的机组开停机计划。

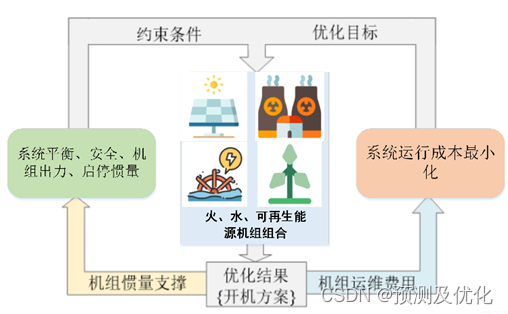
机组组合(Unit commitment, Uc)优化问题旨在电力系统运行时，安全给定以及调整发电机组的启/停与实时出力，使发电机组的总运行成本最小。研究UC问题的混合整数规划方法，主要涉及机组组合模型紧且简洁的重构--紧性能减少求解器搜索空间，简洁性提高求解器搜索速度，研究的机组模型能显著减少计算负担。此外，研究机组组合完全分布式优化方法，通过对偶完全解耦机组系统约束，在完全保护机组隐私信息前提下，获得高质量的机组调度方案。

模型紧凑/简洁性描述

安全约束机组组合(Security Constrained Unit Commitment，简称SCUC)是一种基于电力系统安全性约束条件下的发电机组优化组合问题。在电力系统运行中，为了保证电力供应的安全性，需要对发电机组的开启和关闭状态进行优化调度。SCUC问题就是在满足电力系统安全约束的前提下，寻找一组最优的发电机组组合，使得系统的运行成本最低或经济效益最大。

SCUC与考虑约束的经济调度(SCED)的区别

SCUC与考虑约束的经济调度(Screening-based Constrained Economic Dispatch，简称SCED)都是电力系统优化调度问题，但它们之间存在一些区别:

1.优化目标:SCUC问题的优化目标是在满足安全约束条件下，寻找组发电机组组合，使得系统的运行成本最低或经济效益最大;而SCED问题则是在满足电力系统可靠性和经济性约束条件下，寻找一组最优的发电机组组合。

2.约束条件:SCUC问题主要考虑电力系统的安全性约束，包括功角约束、电压约束等;而SCED问题除了考虑安全性约束外，还需要考虑经济性约束，如燃料成本、排放约束等。

3.应用背景:SCUC问题主要应用于电力系统的安全稳定运行，如防止电力系统故障、确保电力供应可靠性等;而SCED问题则更多应用于电力市场的优化调度，如发电机组的调峰、备用容量管理等。

程序简介

程序综合分析了机组发电量约束及安全校正计算的特点，提出了一种有效的处理方法，通过修正机组出力可调整量约束，将发电量约束隐含于各越限时段的建模和计算过程中，考虑系统运行的故障情况，在安全校正计算完成后自然得到满足。程序算例丰富、注释清晰、干货满满，可扩展性和创新性很高！下面对文章和程序做简要介绍！

建模步骤

SCUC是根据研究周期内的各个时段系统负荷预测优化机组发电计划，包括机组起停方式和机组发电出力。优化的目标是系统的总成本(包括发电成本、开机成本、停机成本)最小。约束主要分为3类：

(1)系统约束。包括负荷平衡、系统备用；

(2)机组约束。包括机组出力上下限、最小持续开停时间、爬坡率、旋转备用、最大开停次数；(3)安全约束。包括支路输电极限、断面极限、 节点电压等。SCUC在实际应用中还可以根据需要添加约束条件，如开停机过程的出力约束、分区备用约束、排放约束、资源约束等。

数学模型

电能平衡在UC中有三种不同的表示方式：

在单母线近似中，网格被忽略：只要总产量等于总需求，就认为需求得到满足，无论其地理位置如何。

在DC（直流）近似中，仅对基尔霍夫电流定律建模；这对应于忽略无功功率流，电压角差被认为很小，并且角电压曲线被假定为恒定；

在完整的AC（交流）模型中，使用了完整的基尔霍夫定律：这导致模型中存在高度非线性和非凸约束。当使用全交流模型时，UC实际上包含了最优潮流问题，这已经是一个非凸非线性问题。

本程序考虑AC和DC模型，在AC模型中采用二阶锥模型对机组发电成本做了线性化处理，因此可利用Yalmip+Cplex高效求解。模型中考虑了机组组合故障状态约束，对考虑机组组合故障、电网韧性的小伙伴很有帮助！

程序结果

适用平台：Matlab+Yalmip+Cplex/Gurobi

（1）DC模型：依次为IEEE14节点、30节点、118节点

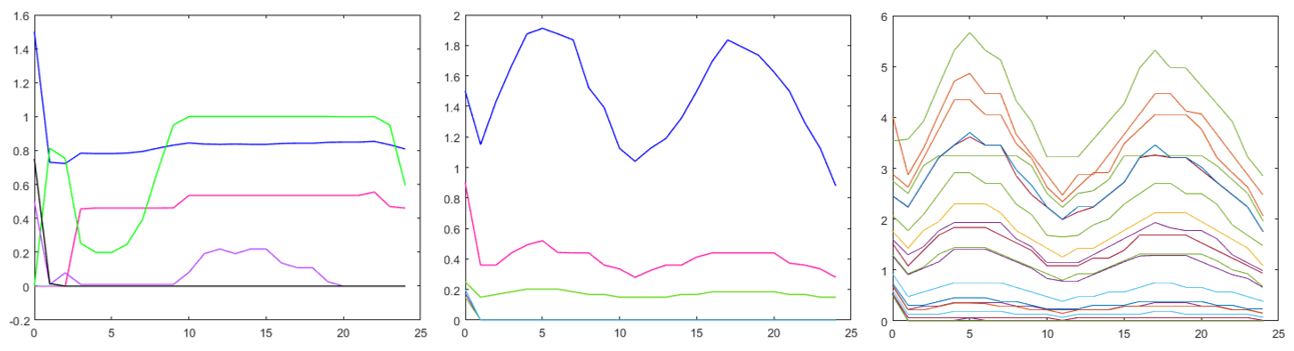
（2）AC模型：依次为IEEE14节点、30节点、118节点

部分程序：

%​% 读入
% casename = input('Please enter case name : ', 's');
% casename = 'case14mod_SCUC';
% casename = 'case30mod';casename = 'case118mod';
k_safe = 0.85;    %安全系数，用于留一定的裕度，针对潮流安全约束​
% 时段数t 用于机组组合优化
n_T = 24;
% 发电机曲线 二次函数 分段线性化
n_L = 20;​
% 初始化文件
initial;PD = bus(:, BUS_PD)/baseMVA;​QD = bus(:, BUS_QD)/baseMVA;
% PD = PD*ones(1, n_T);​% QD = QD*ones(1, n_T);
% 24小时的负荷数据
Q_factor = QD/sum(QD);​P_factor = PD/sum(PD);
%P_sum = sum(PD)-sum(PD)/2*sin(pi/12*[0:n_T-1]+pi/3);
P_sum = mpc.PD'/baseMVA;​QD = Q_factor*sum(QD)*P_sum/sum(PD);
PD = P_factor*P_sum;spnningReserve = 1.02*P_sum;​
%导纳矩阵计算
% [Ybus, Yf, Yt] = makeYbus(baseMVA, bus, M_branch);   % build admitance matrix
[Bbus, Bf, Pbusinj, Pfinj] = makeBdc(baseMVA, bus, branch);       %直流潮流​
% 创建决策变量​% 发电机出力 非发电机节点取0
gen_P = sdpvar(n_bus, n_T);​gen_P_upper = sdpvar(n_bus, n_T);   %发电机有功出力上界
% gen_Q = sdpvar(n_bus, n_T);
% 各节点电压幅值 相角
% Vm = sdpvar(n_bus, n_T);      %幅值
Vm = ones(n_bus, n_T);        %幅值 直流潮流
Va = sdpvar(n_bus, n_T);      %相角​
% 各支路潮流
PF_D = sdpvar(n_branch, n_T);     %P Flow Direct 正向有功潮流 1->2
% QF_D = sdpvar(n_M_branch, n_T);     %Q Flow Direct 正向无功潮流 1->2
% PF_R = sdpvar(n_branch, n_T);     %P Flow Reverse 反向有功潮流 2->1
% QF_R = sdpvar(n_M_branch, n_T);     %Q Flow Reverse 反向无功潮流 2->1​
% 机组状态
u_state = binvar(n_bus, n_T);     %按母线数，非发电机节点取0
C = [];     %约束​% C = sdpvar(C)>=0;
%发电机费用曲线 二次函数分段线性化
P_nl = sdpvar(n_gen, n_L, n_T);​for i = 1: n_gen​gen_P(gen(i,GEN_BUS),t) == sum(P_nl(i,:,t))+gen(i,GEN_PMIN)*u_state(gen(i,GEN_BUS),t)/baseMVA,
​0 <= P_nl(i,l,t) <= (gen(i, GEN_PMAX)-gen(i, GEN_PMIN))/n_L/baseMVA,
​% 机组开机费用 Cjk
cost_up = sdpvar(n_gen, n_T);​C = [C, cost_up >= 0];
​cost_up(:,k) >= start_cost(:,t).*(u_state(gen(:,GEN_BUS),k) - sum(u_state(gen(:,GEN_BUS),[k-t: k-1]),2))

部分内容源自网络，侵权联系删除！

欢迎感兴趣的小伙伴关注并私信获取完整版代码，小编会不定期更新高质量的学习资料、文章和程序代码，为您的科研加油助力！

这篇关于还在被机组组合问题困扰？快来试试这个用处极大的考虑安全约束机组组合模型！的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---