【时间序列】革新Transformer！清华大学提出全新Autoformer骨干网络，长时序预测达到SOTA...

作者 | 吴海旭

报道 | 新智元   编辑 | 好困

【导读】近日，清华大学软件学院机器学习实验室另辟蹊径，基于随机过程经典理论，提出全新Autoformer架构，包括深度分解架构及全新自相关机制，长序预测性能平均提升38%。

尽可能延长预测时效是时序预测的核心难题，对于能源、交通、经济的长期规划，气象灾害、疾病的早期预警等具有重要意义。

清华大学软件学院机器学习实验室的研究人员近日发表了一篇论文，探究了在信息有限的情况下预测更长期未来的这个难题。

针对上述问题，作者大刀阔斧革新Transformer，提出全新的Autoformer模型，在长时序预测方面达到SOTA，在效率性能上均超过Transformer及其变体。

论文链接：https://arxiv.org/abs/2106.13008

研究背景

虽然近期基于Transformer的模型在时序预测上取得了一系列进展，但是Transformer的固有设计，使得在应对长期序列时仍存在不足：

• 随着预测时效的延长，直接使用自注意力（self-attention）机制难以从复杂时间模式中找到可靠的时序依赖。

• 由于自注意力的二次复杂度问题，模型不得不使用其稀疏版本，但会限制信息利用效率，影响预测效果。

作者受到时序分析经典方法和随机过程经典理论的启发，重新设计模型，打破Transformer原有架构，得到Autoformer模型：

• 深度分解架构：突破将时序分解作为预处理的传统方法，设计序列分解单元以嵌入深度模型，实现渐进式地（progressively）预测，逐步得到可预测性更强的组分。

• 自相关（Auto-Correlation）机制：基于随机过程理论，丢弃点向（point-wise）连接的自注意力机制，实现序列级（series-wise）连接的自相关机制，且具有 的复杂度，打破信息利用瓶颈。

• 应对长期预测问题，Autoformer在能源、交通、经济、气象、疾病五大领域取得了38%的大幅效果提升。

方法介绍

作者提出了Autoformer模型，其中包括内部的序列分解单元、自相关机制以及对应的编码器、解码器。

（1）深度分解架构

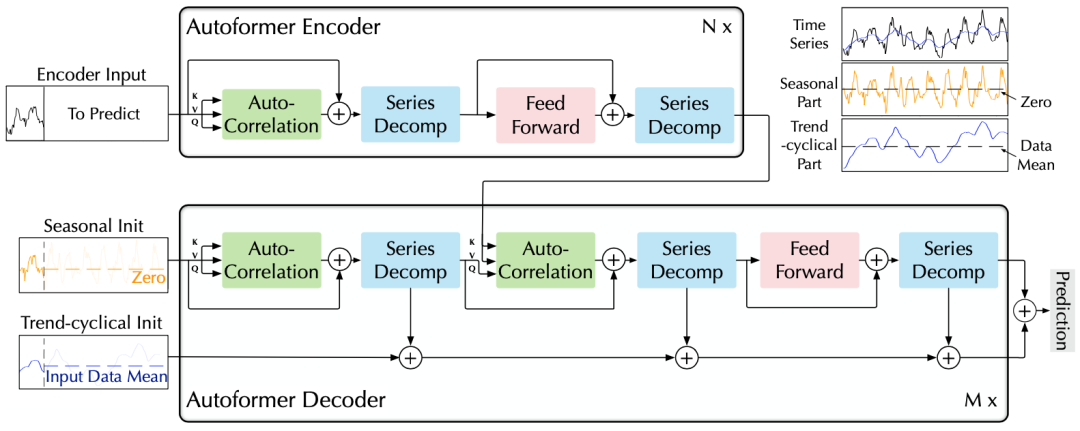
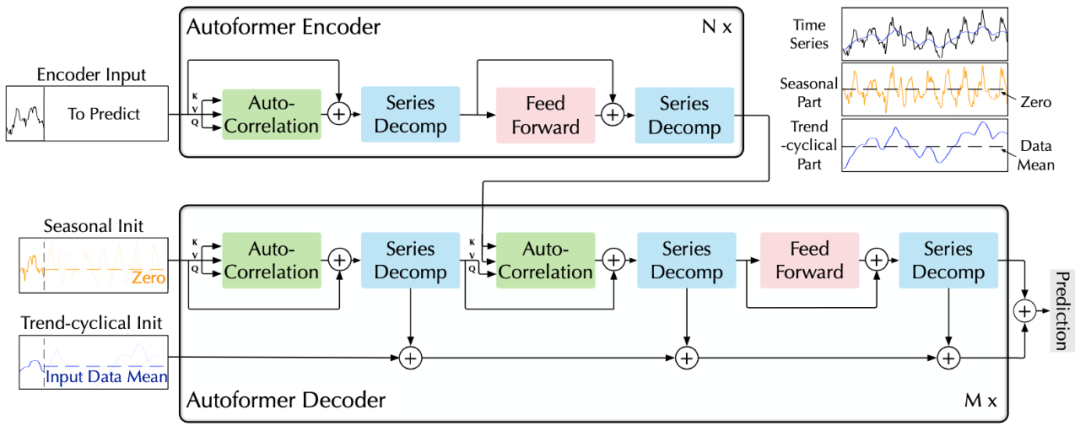
Autoformer架构

时间序列分解是时序分析的经典方法，可以将时间序列分解为几类潜在的时间模式，如周期项，趋势项等。

在预测任务中，由于未来的不可知性，通常先对输入进行分解，再每个组分分别预测。

但这样使得预测结果受限于分解效果，并且忽视了长期未来中各个组分之间的相互作用。

针对上述问题，作者提出深度分解架构，在预测过程中，逐步从隐变量中分离趋势项与周期项，实现渐进式（progressive）分解。

并且模型交替进行预测结果优化和序列分解，可以实现两者的相互促进。

A. 序列分解单元

基于滑动平均思想，平滑时间序列，分离周期项与趋势项：

其中， 为待分解的隐变量， 分别为趋势项和周期项，将上述公式记为。

B. 编解码器

编码器：通过上述分解单元，模型可以分离出周期项 ， 。而基于这种周期性，进一步使用自相关机制（ ），聚合不同周期的相似子过程：

解码器：对趋势项与周期项分别预测。

• 对于周期项，使用自相关机制，基于序列的周期性质来进行依赖挖掘，并聚合具有相似过程的子序列；

• 对于趋势项，使用累积的方式，逐步从预测的隐变量中提取出趋势信息。

（2）自相关机制

观察到，不同周期的相似相位之间通常表现出相似的子过程，利用这种序列固有的周期性来设计自相关机制，实现高效的序列级连接。

自相关机制包含基于周期的依赖发现（Period-based dependencies）和时延信息聚合（Time delay aggregation）。

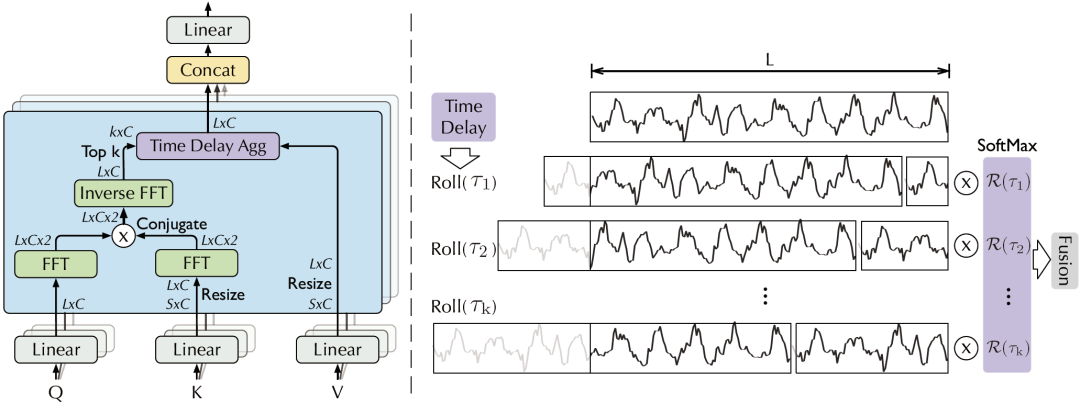
A. 基于周期的依赖发现

基于上述观察，为找到相似子过程，需要估计序列的周期。基于随机过程理论，对于实离散时间过程 ，可以如下计算其自相关系数 ：

其中，自相关系数 表示序列 与它的 延迟 之间的相似性。

在自相关机制中，将这种时延相似性看作未归一化的周期估计的置信度，即周期长度为 的置信度为 。

实际上，基于Wiener-Khinchin理论，自相关系数 可以使用快速傅立叶变换（FFT）得到，其计算过程如下：

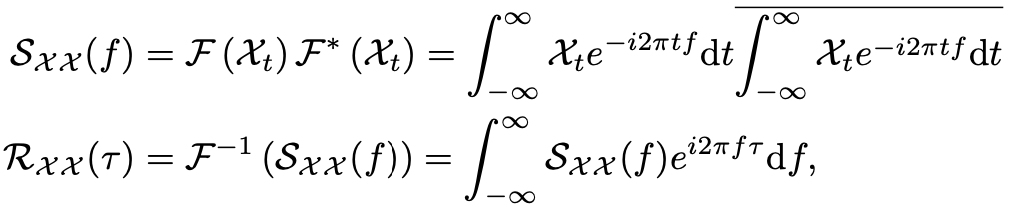
其中， 和 分别表示FFT和其逆变换。因此，复杂度为 。

B. 时延信息聚合

为了实现序列级连接，还需要将相似的子序列信息进行聚合。自相关机制依据估计出的周期长度，首先使用 操作进行信息对齐，再进行信息聚合：

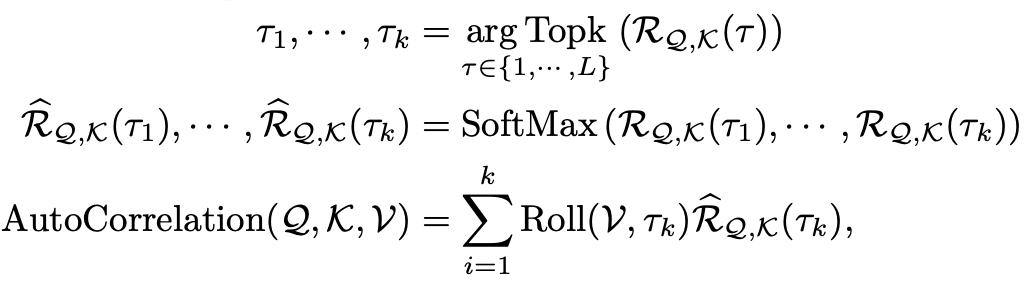
这里，依然使用query、key、value的多头形式，从而可以无缝替换自注意力机制。

同时，挑选最有可能的 个周期长度，用于避免融合无关、甚至相反的相位。整个自相关机制的复杂度仍为 。

C. 对比分析

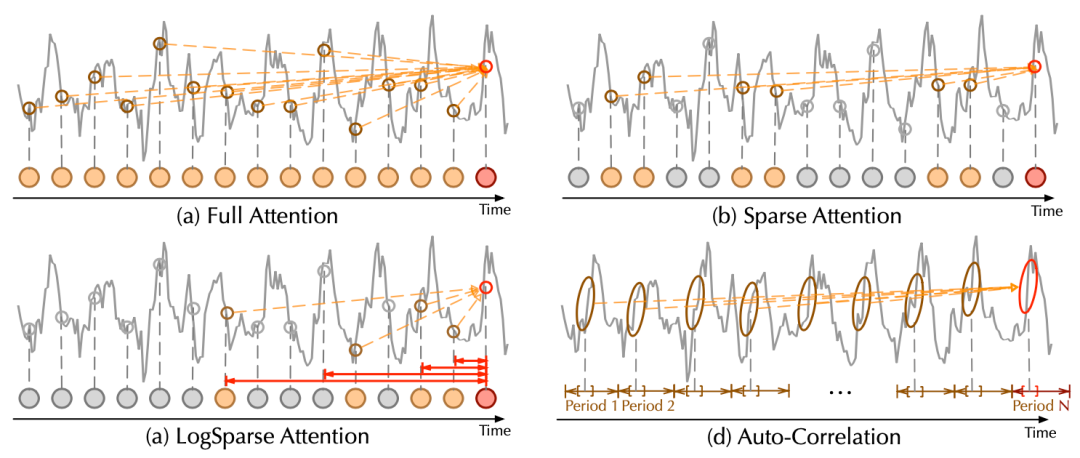
自相关机制与自注意力机制对比

相比于之前的点向连接的注意力机制或者其稀疏变体，自注意力（Auto-Correlation）机制实现了序列级的高效连接，从而可以更好的进行信息聚合，打破了信息利用瓶颈。

实验

作者在6个数据集上进行了测试，涵盖能源、交通、经济、气象、疾病五大主流领域。

(1) 主要结果

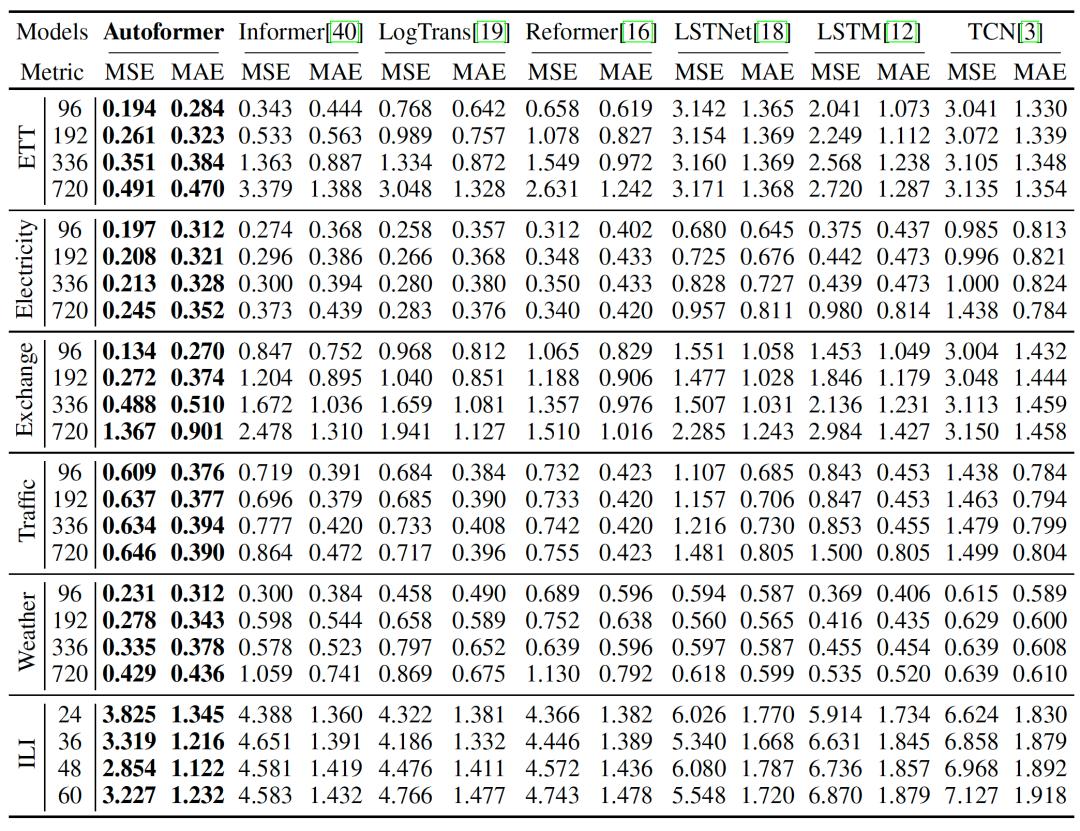整体实验结果

Autoformer在多个领域的数据集、各种输入-输出长度的设置下，取得了一致的最优（SOTA）结果。

在input-96-predict-336设置下，相比于之前的SOTA结果，Autoformer实现了ETT能源数据集74%的MSE提升，Electricity能源数据集MSE提升24%，Exchange经济数据集提升64%，Traffic交通数据集提升14%，Weather气象数据集提升26%，在input-24-predict-60设置下，ILI疾病数据集提升30%。

在上述6个数据集，Autoformer在MSE指标上平均提升38%。

(2) 对比实验

深度分解架构的通用性：将提出的深度分解架构应用于其他基于Transformer的模型，均可以得到明显提升，验证了架构的通用性。

同时随着预测时效的延长，提升效果更加明显，这也印证了复杂时间模式是长期预测的核心问题。

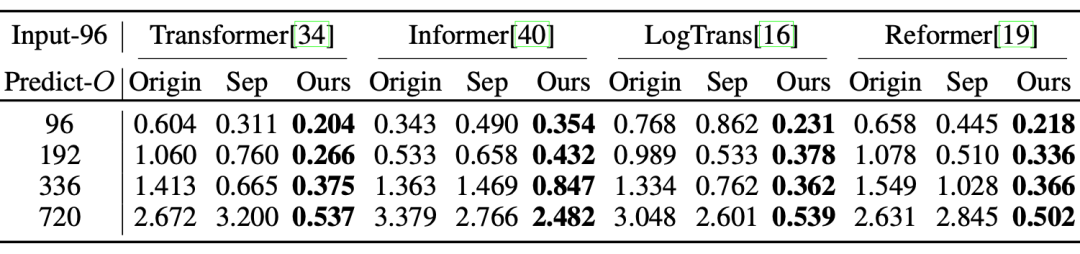
ETT数据集上的MSE指标对比，Origin表示直接预测，Sep表示先分解后预测，Ours表示深度分解架构。

自相关机制 vs. 自注意力机制：同样基于深度分解架构，在众多输入-输出设置下，自相关机制一致优于自注意力机制及其变体，比如经典Transformer中的Full Attention，Informer中的PropSparse Attention等。

ETT数据集上对比实验，将Autoformer中的自相关机制替换为其他自注意力机制，得到上述结果。

(3) 模型分析

时序依赖可视化：

对于序列的最后一个时间点，各模型学到的时序依赖可视化，图(a)中红色线表示学习到的过程的位置。

通过上图可以验证，Autoformer中自相关机制可以正确发掘出每个周期中的下降过程，并且没有误识别和漏识别，而其他注意力机制存在缺漏甚至错误的情况。

效率分析：

效率对比，红色线为自相关机制

在显存占用和运行时间两个指标上，自相关机制均表现出了优秀的空间、时间效率，两个层面均超过自注意力机制及其稀疏变体，表现出高效的 复杂度。

总结

针对长时序列预测中的问题，作者基于时序分析的经典方法和随机过程的经典理论，提出了基于深度分解架构和自相关机制的Autoformer模型。

Autoformer通过渐进式分解和序列级连接，应对复杂时间模式以及信息利用瓶颈，大幅提高了长时预测效果。

同时，Autoformer在五大主流领域均表现出了优秀的长时预测结果，模型具有良好的效果鲁棒性，具有很强的应用落地价值。

参考资料：

https://arxiv.org/abs/2106.13008

公众号：AI蜗牛车

保持谦逊、保持自律、保持进步

个人微信

备注：昵称+学校/公司+方向

如果没有备注不拉群！

拉你进AI蜗牛车交流群