人工智障：神经网络入门-传统感知模型(McCulloch-Pitts与Rosenblatt感知模型)

有道云笔记持续更新：

文档：1.函数感知器.note
链接：http://note.youdao.com/noteshare?id=1b26a31ef01fac6ecf0b147f66511807&sub=32BBDE8AD2384ED79A62B1A94E57F36C

McCulloch-Pitts模型

 神经元细胞图

        输入信号通过树突（自变量）进入神经元，再通过轴突（因变量）输出结果。如果输入只有一个，那么对应的输出也只有一个，也就是一元函数。但是往往一个问题需要考虑多个方面，我们可以用下面的图来表示多个方面的问题；

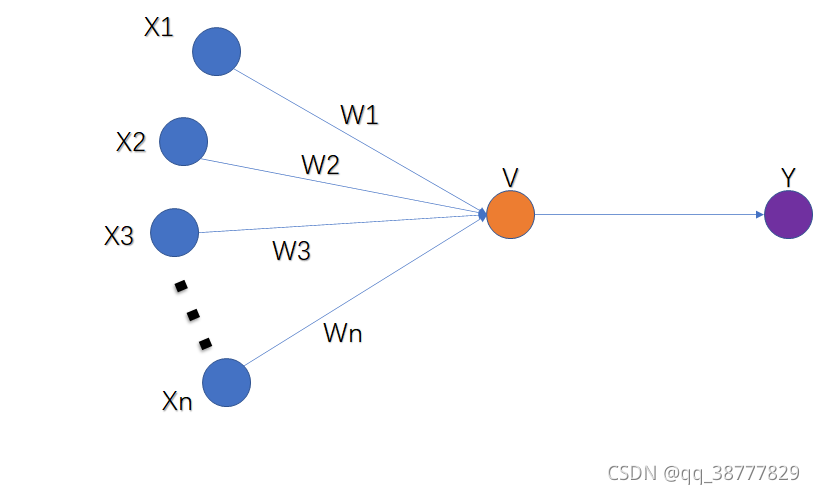
McCullon-Pitts模型示意图

        可以将直觉看作一个多元函数，即 Y = X1*W1 + X2*W2 + X3*W3 + ... + Xn*Wn ；

        其中，X为问题的自变量，W为该自变量所占的权值；在该模型中，权值W是提前设置好的，这样做显然存在问题。当W设置的值不合理的时候，感知是无法做到准确。如何去这只这个W呢？

Rosenblatt感知模型

        为了将“直观的直觉”转换为“现实认知”，在McCullon-Pitts模型的基础上，让神经元自己调整权值W。

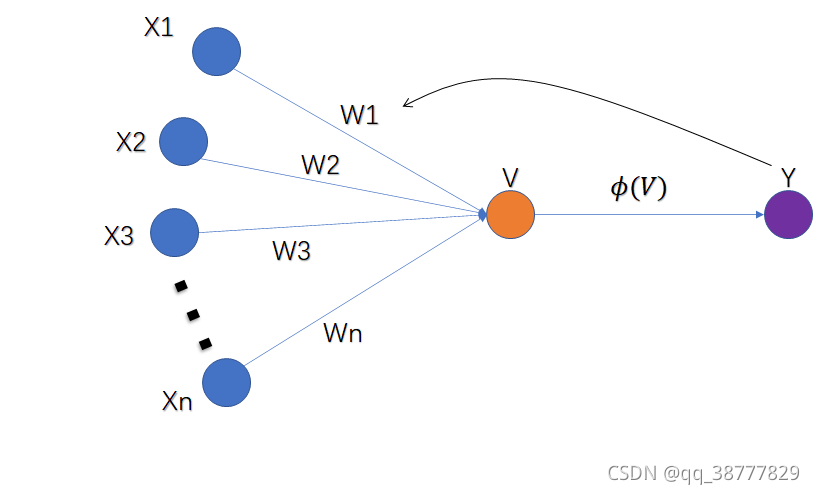
 Rosenblatt模型示意图

t为了让我们更好地理解模型，我们想在将模型简化为一个变量。

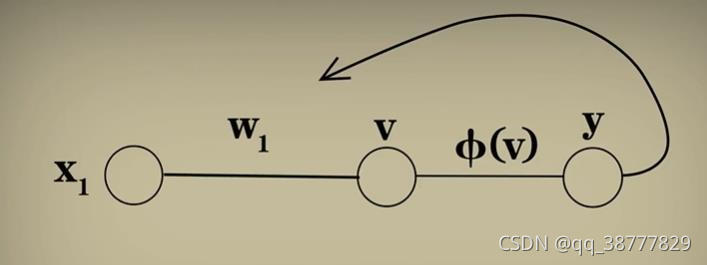
模型的算法步骤如下：

1.根据一个输入得到 y，用 标准值 - y = 误差；

2.将 W1 = W1+误差，再执行 步骤1 ；

这便是Rosenblatt模型的学习过程。当然它还需要处理一下细节问题。

当输入X为负数时

当输入为负，如果仍然用（W = W+误差）来调整W，那么调整后的结果将会越来越远离我们的标准结果；所以我们引入了 W = W + X*误差；这样就巧妙得避免了这个问题；

当W调整过大时

W调整也是有变化幅度的，如果W的变化幅度过大，那么可能会使计算的结果在标准结果上来回跳跃；所以我们引入了 W = W + X * 误差 * alpha

感知器收敛定理的证明

        如果要验证这个模型的正确性，即我们需要去证明其结果是否收敛，是否有结果；下面是其收敛性的证明，图片来源于：Ele实验室

梯度下降和反向传播