本文主要是介绍Rectified Linear Units, 线性修正单元激活函数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
ReLU
在神经网络中,常用到的激活函数有sigmoid函数:
ReLU函数可以表示为
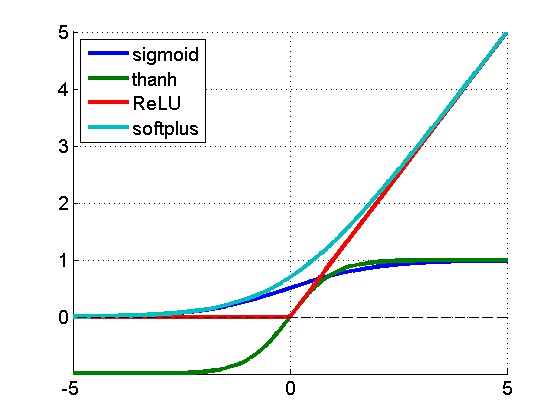
sigmoid、tanh、ReLU、softplus的对比曲线如下图所示:
使用ReLU函数时,有几个重要的优点和缺点:
1. [优点]和sigmoid、tanh神经元昂贵的操作(指数等)相比,ReLU可以通过简单的零阈值矩阵进行激活,并且不受饱和的影响
2. [优点]和sigmoid、tanh函数相比,ReLU可以大大加快随机梯度下降算法的收敛,普遍认为原因在于其具有线性、非饱和的形式
3. [缺点]不幸的是,ReLU在训练时是非常脆弱的,并且可能会“死”。例如,流经ReLU神经元的一个大梯度可能导致权重更新后该神经元接收到任何数据点都不会再激活。如果发生这种情况,之后通过该单位点的梯度将永远是零。也就是说,ReLU可能会在训练过程中不可逆地死亡,并且破坏数据流形。例如,如果学习率太高,你可能会发现,多达40%的网络会“死”(即,在整个训练过程中神经元都没有激活)。而设置一个适当的学习率,可以在一定程度上避免这一问题。
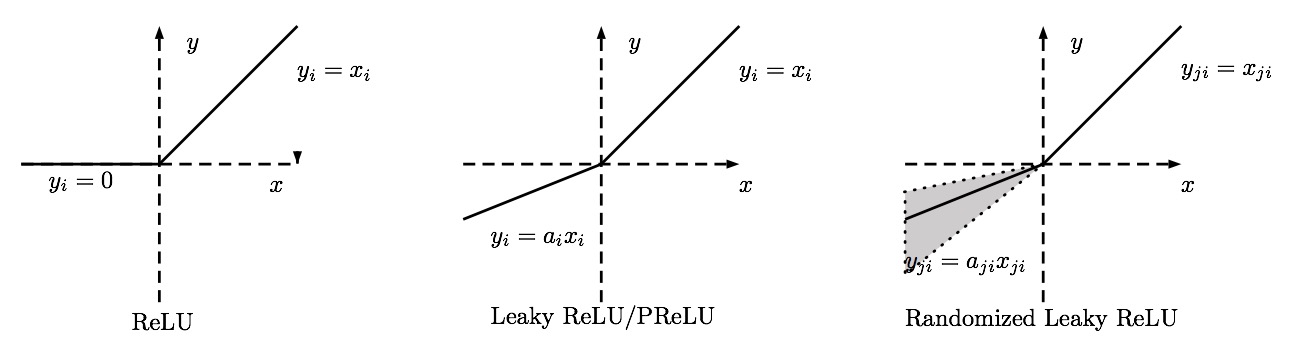
ReLU还存在一些变体,如图所示:
概述如下:
Noisy ReLU
在ReLU中包含高斯噪声,便可以得到noisy ReLU:
Leaky ReLU
Leaky ReLU是对于“ReLU死亡问题”的一次解决尝试
可以表示为:
其中,a为一个较小值,如0.01等
有研究表明采用这种形式的激活函数效果更好,但结果并不总是一致的
优势:
1. Biological plausibility:单边,相比于反对称结构(antisymmetry)的tanh
2. Sparse activation:基本上随机初始化的网络,只有有一半隐含层是处于激活状态,其余都是输出为0
3. efficient gradient propagation:不像sigmoid那样出现梯度消失的问题
4. efficient computation:只需比较、乘加运算。使用rectifier 作为非线性激活函数使得深度网络学习不需要pre-training,在大、复杂的数据上,相比于sigmoid函数等更加快速和更有效率。
Randomized Leaky ReLU
对于RReLU,训练过程中负数部分的斜坡是在一个范围内随机选取的,然后在测试过程中固定。在最近的Kaggle National Data Science Bowl (NDSB) 竞赛中,据悉RReLU由于其随机的特性可以有效地减少过拟合。
Conclusion
ReLU的各种变体在一定程度上都超越了原始的ReLU,而PReLU和RReLU似乎是更好的选择
—————————————————————————–
Web Reference
[1]Rectified Linear Unit (ReLU)
[2]修正线性单元(Rectified linear unit,ReLU)
[3][20140429] Rectified Linear Units
这篇关于Rectified Linear Units, 线性修正单元激活函数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!