论文解读分析：ML-KELM: A Kernel Extreme Learning Machine Scheme for Multi-Label Classification of Real Time

关键词

KELM,C-IL,E-IL,Muti-label

技术难点

1. 流式机器学习相比于批式机器学习来说有一下几个难点：

• 机器学习训练模型的时候数据只通过一次
• 概念漂移和新概念（新类型）问题很难处理

2. 多标签分类的输出空间太大了

• 如果有10个标签，那么输出空间就是

3. 标签增量学习很困难

• 假如一个模型被训练出来分类动物，如果有一天我们把训练数据改成汽车，那么训练之后，模型会“遗忘”如何分类动物

论文攻关方案

多标签问题描述

• 原文如下
  The main task of multi-label classification is to establish a bridge that connects the instance to category labels. Let X ⊂ Rd denotes a d-dimensional instances space. The set F = {F1, F2, . . . , Fq} is the output space of q possible labels. Each instance xi = [xi,1, xi,2, . . . , xi,d] is associated with a subset of labels Yi = [yi,1, yi,2, . . . , yi,q] = {−1, 1}q. yi,j = 1 only if the jth label Fj is associated with instance xi, and −1 otherwise.
• 大白话
  一个数据样本被放入模型之后的输出数据是一组向量，向量里的每一个维度代表一个标签。向量里面的值分为-1或1.当值为1的时候说明这个数据具有这个标签，否则没有。
• 举例
  一个人的各种具体数据被放进了模型中，得到了一个二维向量。第一个维度表示高，第二个维度表示胖。当输出向量为[-1,1]的时候，这个人就有“胖”这个标签，且不具有“高”的标签。

ML-KELM模型结构如下

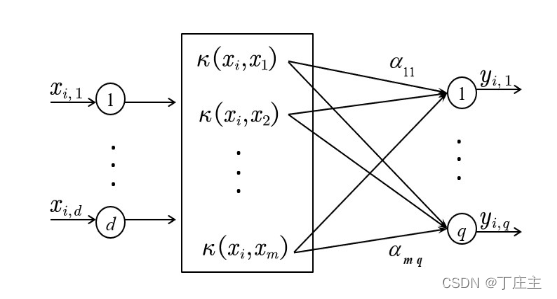
从ELM到KELM

ELM

点击进入参考链接

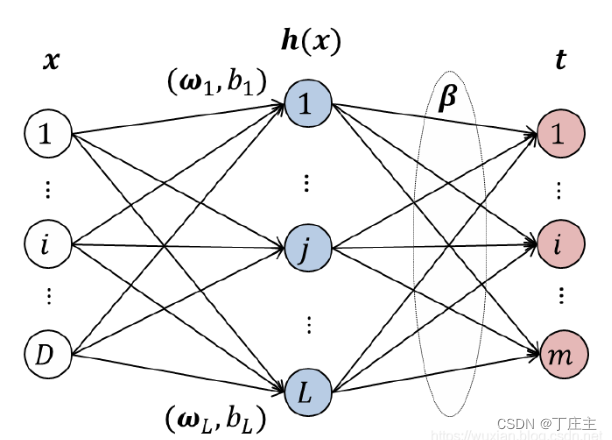
我们先随机复制给输入层到隐藏层之间的权重和偏置。然后为隐藏神经元h(x)选择合适的激活函数g(x)

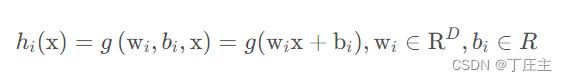
为了达到我们训练的目的，即隐藏层节点在经过隐藏层和输出层之间的权重参数计算之后，与我们训练数据集期望的分类结果的误差最小。我们建立如下等式：

在考虑了模型性能之后，我们选择加入正则项来提升预测性能。得到如下结果：

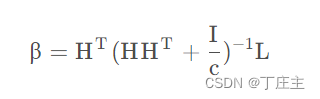
L是训练数据集的标签集合。例如我们有4个训练数据，每个训练数据最多5个标签。那么L就是一个4*5的矩阵

KELM

当我们得到了B层通向输出的各个权重的时候，我们就可以进行预测了。对第K个样本进行预测。模型如下：

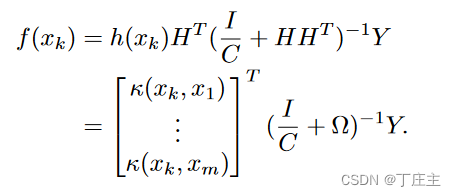
我们可以通过核函数极大的减小计算量，我们上面式子第一个等号旁边是将xk经过h(x)这个仿射函数提升到高维空间（也即是将输入数据经过权重偏置计算之后在隐藏神经元的输出）

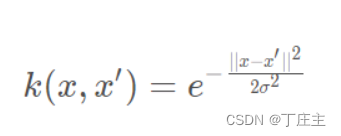
注：这里是m个训练数据

threshold的问题

我们通过先前的步骤得到了输出向量，问题来了。我们的标签使用-1和1来表示的。但是在外面经过上面的计算之后得到的是一个用实数表示的向量。

比如我们有高和胖这两个标签，
[1,1]表示这个样例有“高”和“胖”这个标签（也可以里说成是这个样本与“高”和“胖”这两个标签相关）；[-1,-1]表示没有这两个标签（也可以里说成是这个样本与“高”和“胖”这两个标签无关）。
但是我们得到的输出向量是[0.7,0.8]，那这算怎么回事儿？

所以，我们还需要来找出一个threshold来区分一个样例的输出到底哪些是相关标签，哪些不是。
比如我们通过技术手段算出来上面的例子的threshold是0.75.那么这个样例的输出0.8>0.75就代表相关，那就是“胖”，否则就是不相关。最后[0.7,0.8]这个输出向量就是[-1,1].

threshold的选定方案

先给出算法

解释如下：我们需要根据训练数据集算出核矩阵和正则项，这也就意味着我们的初步模型直接建好了

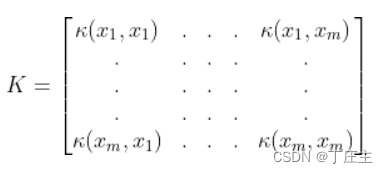
然后再将一条条训练数据放进去预测，得到用实数表示的标签的输出向量。
紧接着，我们将每一个维度拿出来和Y（真实标签，用-1和1表示的），若是哪个维度的实数是1，就代表相关，就将这个实数放入一个叫S的集合里面，否则放入另一个S的集合里面。我们将相关集合S的最小值和不相关集合的最大值取出来做均值。就得到了S(xi).先别急，我们这样定义threshold：

threshold(x)=<a,f(x)>+b

但是我们为了让这个threshold表现得好，那就要选最好得a向量和b偏置。我们如下定义问题：

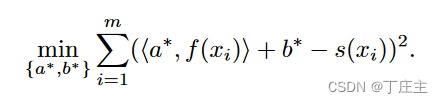
解出a向量和b偏置之后我们就可以用threshold来做测试了，
我们测试集D′ = {(xi, Yi)|1 ≤ i ≤ m′ }，每条数据相关标签最多q个也就是输出为全1的9维向量，那么最后我们得到的所有测试集的输出f(x)为m’*q.
E其实就是个m’*1的矩阵（里面全是1，用来让偏置b参与计算的），把问题定义成如下矩阵形式：

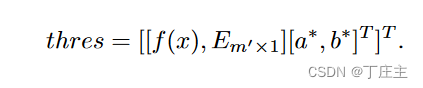
最后得到了一个m’维的向量，然后我们比较1<=i<=m’的样本的输出向量，如果输出向量里面的实数大于thres（i），那么我们把这个实数改为1，否则改为-1.最后如下：

最后也就达到了我们的预测目的。

超大矩阵带来的新问题

刚刚我们已经把多标签分类问题解决了。我们再来回顾一下，我们的隐藏层的输出网络的权重可以如下表示：

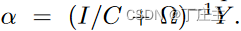
其中

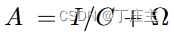
我们可以用Cholesky矩阵分解发将矩阵可以做如下转化，其中L和P是下三角矩阵：

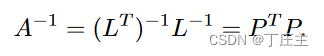
其中L可由如下得到：

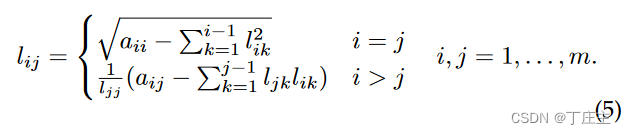
P可由如下得到：

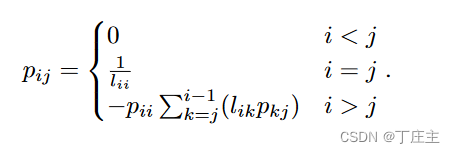
我们通过上面的算法来求矩阵的逆可以减小一半的时间。

但是还有一个计算可行性的问题，比如我们的核矩阵是存的double类型的数据，这个核矩阵80000*80000.我们算了一下，这样的矩阵占了将近50个G的内存，而且还要求逆矩阵，我们不打算将这个问题交给个人电脑来做，我们用分布式的思路来做。
将A做如下切割转化：



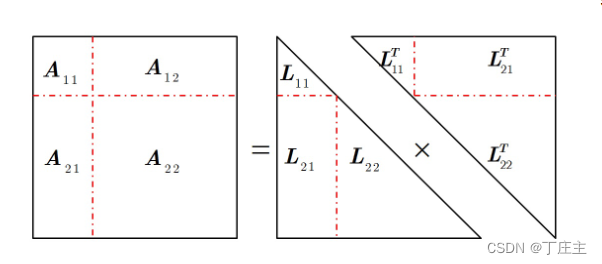
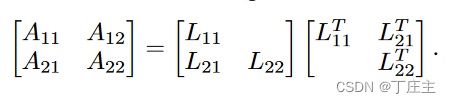
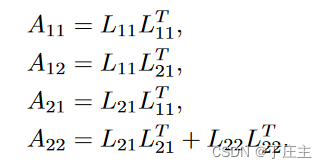
梳理一下我们为了做超大矩阵的逆矩阵需要做些啥事儿。首先，我们先用一个单机结点能做的A11用Cholesky矩阵分解法来算出L11，然后将A12和L11配合计算出L21（因为被分解，所以我们也姑且认为单机节点可以将A12放入内存）。当然，A22也可能大到无法直接放入内存计算，所以我们可以用递归思想来做这个问题。以此类推，我们最终可以算出L11，L21，L22。得到了这三个矩阵之后我们也可以得到L和P，最终我们通过分布式计算出了A的逆矩阵。

Online example-incremental learning

在机器学习领域，增量学习致力于解决模型训练的一个普遍缺陷：「灾难性遗忘(catastrophic forgetting)」 ，也就是说，一般的机器学习模型(尤其是基于反向传播的深度学习方法)在新任务上训练时，在旧任务上的表现通常会显著下降。所以，我们的接下来的目标就是如何做到在学习新知识的同时能够保留对旧知识的判断，甚至是优化对旧知识的理解。

本篇论文给出如下方案：

没有进行增量训练的时候，我们的输出权重如下表示：

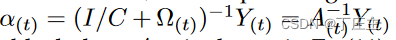
其中

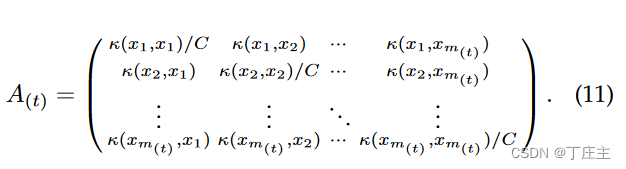
At表示第t批训练数据集的训练出来的权重。

回过头了梳理一下，我们训练的实质是什么，其实就是更新隐藏层的输出权重的逆矩阵和Y。流式数据计算平台都有滑动窗口的概念，这个概念也能帮助我们进行训练，我们将新的训练数据放进滑动窗口累计到一定数目之后形成新批次的数据，放进模型进行增量训练。更新后的隐藏层输出权重矩阵如下：

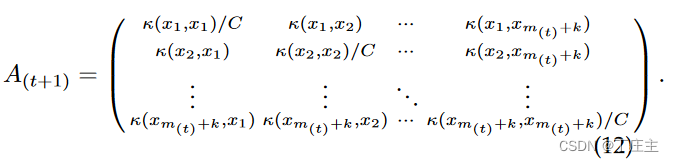
同时也可以如下表示：

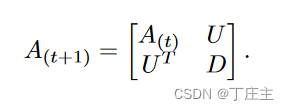
其中U和D如下表示：

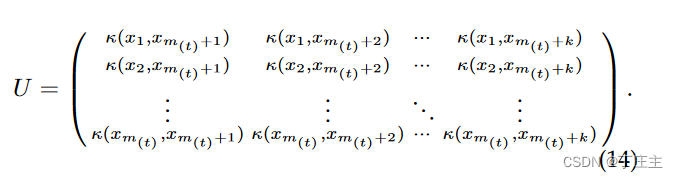
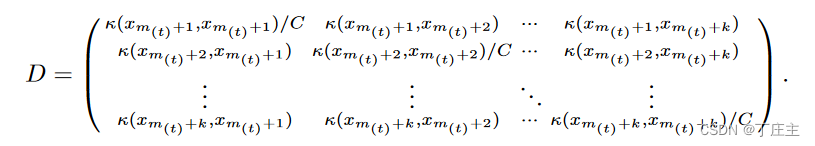
我们通过Sherman-Morrison-Woodbury 算法来计算A(t+1)的逆矩阵，表示如下：

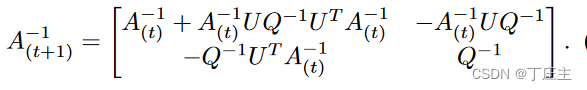
其中Q如下表示：

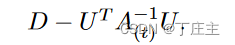
从而在新数据到来时我们可以通过A(t+1)和Y(t+1)来更新隐藏层输出权重，达到增量学习的目的。

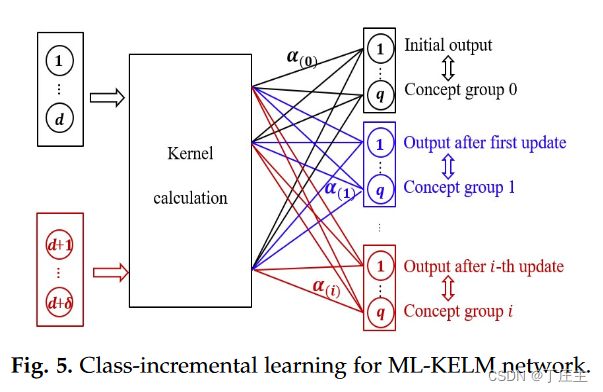
Online class-incremental learning

上面我们提到了Online example-incremental learning(E-IL)，接下来我们需要解决的就是C-IL问题。比如我们的机器通过数据训练的习得了如何识别“高”和“胖”这两个标签，但是我们如果新数据有一个“好”这样的新标签呢？也就是我们的数据类别标签增加了。我们的模型如何判断出来有新标签？如何区分新标签有哪些？如何对现有的学习模型进行扩展，增强学习能力？

本篇论文给出如下方案：

首先是关于判断数据是否具有新标签和新类别。因为我们测试和训练的数据的输出是一个由-1和1构成的向量，1代表相关，-1代表不相关。所以当我们的输出向量的每个维度全都是-1的时候，我们就认为这条数据是一个新类别，有新标签。

接着，我们将这条数据放入缓冲区囤积起来，等到囤积的数目达到我们预设的值的时候，我们就将这批囤积起来的数据进行聚类操作。生成m个新的标签。然后用LRU算法来淘汰一些标签，让我们的标签数量始终维持在一个数目。

最后，我们新标签的出现很大可能是因为有了新特征。就比如原先的输入特征是[身高数，体重数]，现在的输入特征是[身高数，成绩分数]。所以，我们需要在输入层加入新的特征变为[身高数，体重数，成绩分数]，也就是输入特征向量的维度增加了。

经过上述的方案之后我们分析为什么这样的方式可以能够让模型对旧知识的分类能力不被新知识的灌输所影响呢？我们可以看到，我们决策取决于我们的输出权重：

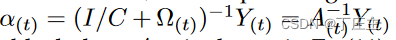
这个矩阵的大小是随着新来的训练数据所动态变化的，旧知识所决定的矩阵数值是不会改变的，新来的知识会改变矩阵的大小，将原来旧知识构造的矩阵尺寸变大，然后再里面填充数据（也就是正则化后的核矩阵的数值）。