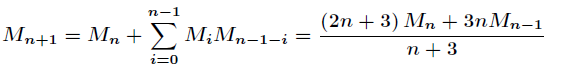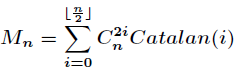几种数学公式(环排列 母函数 唯一分解定理 卡特兰数 默慈金数 贝尔数 那罗延数)

2023-10-20 02:10
文章标签 函数 定理 几种 卡特兰 唯一 分解 排列 数学公式 默慈金数 那罗延数 贝尔

本文主要是介绍几种数学公式(环排列 母函数 唯一分解定理 卡特兰数 默慈金数 贝尔数 那罗延数)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一：环排列

把一个m个元素的环在m个不同的位置拆开记得到m个不同的线排列。由于n个不同元素中任取m个元素的排列方法为P(n,m)种，所以n个不同元素中任取m个元素的环排列方法有P(n,m)/m种。(p是排列组合中的A)
特别的，n个不同元素的环排列方法有P(n,n)/n=(n-1)！种。

二：母函数（用来解决：有N种重量的物品，每种物品有M个(1-无穷),求可以组合出来的重量的个数和该重量的方案数。）

题意：火星上的货币有1,4,9,16,25.....17^2这17中面值的硬币，问任意给定一个不大于300的正整数面额，用这些硬币来组成此面额总共有多少种组合种数。

2
10
30
0

Sample Output

1
4
27
#include<cstdio>
#include<iostream>
using namespace std;
const int MAXN = 300 + 10;
int a[MAXN];
int b[MAXN];
int main()
{int n;while(cin >> n && n){for(int i = 0; i <= 300; i++) // 初始化{a[i] = 1; // 模拟第一个括号，各项的系数为1b[i] = 0; // 中间数组}for(int i = 2; i <= 17; ++i) // 外层括号数{for(int j = 0; j <= n; ++j) // 因为没有限制硬币的数量，每步新形成的括号，{for(int k = 0; k + j <= n; k += i * i) 增量。{b[k + j] += a[j];}}for(int j = 0; j <= n; ++j) // 因为{ a[j] = b[j];b[j] = 0;}}cout << a[n] << endl;}return 0;
}

三：唯一分解定理

<1>容斥原理 

容斥原理中经常用到的有如下两个公式：

1.两集合的容斥关系公式：A∪B＝A＋B－A∩B。

2.三个集合的容斥关系公式：A∪B∪C＝A＋B＋C－A∩B－A∩C－B∩C＋A∩B∩C。

需要注意的是，以上两个公式分别主要针对两种情况：第一个公式是针对涉及到计算两类事物的个数，第二个公式是针对涉及到三类事物的个数。

<2>抽屉原理

桌上有十个苹果，要把这十个苹果放到九个抽屉里，无论怎样放，我们会发现至少会有一个抽屉里面至少放两个苹果。这一现象就是我们所说的“抽屉原理”。 抽屉原理的一般含义为：“如果每个抽屉代表一个集合，每一个苹果就可以代表一个元素，假如有n+1个元素放到n个集合中去，其中必定有一个集合里至少有两个元素。” 抽屉原理有时也被称为鸽巢原理。它是组合数学中一个重要的原理。

四：卡特兰数

实际上就是出栈序列的种数

令h(0)=1,h(1)=1，catalan数满足递推式:

h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)

例如:h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2

h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5

另类递推式:

h(n)=h(n-1)*(4*n-2)/(n+1);

递推关系的解为:

h(n)=C(2n,n)/(n+1) (n=0,1,2,...)

递推关系的另类解为:

h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)

eg:

As we all know the Train Problem I, the boss of the Ignatius Train Station want to know if all the trains come in strict-increasing order, how many orders that all the trains can get out of the railway.

Input

The input contains several test cases. Each test cases consists of a number N(1<=N<=100). The input is terminated by the end of file.

Output

For each test case, you should output how many ways that all the trains can get out of the railway.

Sample Input

1
2
3
10

Sample Output

1
2
5
16796
Hint
The result will be very large, so you may not process it by 32-bit integers.
//h(n)=h(n-1)*(4*n-2)/(n+1)
#include<cstdio>
#include<algorithm>
#include <iostream>
using namespace std;
typedef long long ll;
ll a[105][100];
void f()
{ll i,j,yu,len;a[2][0]=1;a[2][1]=2;a[1][0]=1;a[1][1]=1;len=1;for(i=3;i<101;i++){yu=0;for(j=1;j<=len;j++){ll t=(a[i-1][j])*(4*i-2)+yu;yu=t/10;a[i][j]=t%10;}while(yu){a[i][++len]=yu%10;yu/=10;}for(j=len;j>=1;j--){ll t=a[i][j]+yu*10;a[i][j]=t/(i+1);yu = t%(i+1);}while(!a[i][len])len--;a[i][0]=len;}}
int main()
{f();ll n,i;while(scanf("%d",&n)!=EOF){for(i=a[n][0];i>0;i--)printf("%lld",a[n][i]);puts("");}return 0;
}

再来一个例题

As we all know the Train Problem I, the boss of the Ignatius Train Station want to know if all the trains come in strict-increasing order, how many orders that all the trains can get out of the railway.

Input

The input contains several test cases. Each test cases consists of a number N(1<=N<=100). The input is terminated by the end of file.

Output

For each test case, you should output how many ways that all the trains can get out of the railway.

Sample Input

1
2
3
10

Sample Output

1
2
5
16796由于满足1 2 5 所以为卡特兰数  又因为数比较大  所以用java写    要学java  看这喽https://blog.csdn.net/zcy19990813/article/details/81173275            https://blog.csdn.net/zcy19990813/article/details/81173071
import java.math.BigInteger;
import java.util.Scanner;
import java.io.*;
public class Main{public static void main(String args[]) {Scanner cin=new Scanner(System.in);int n;while(cin.hasNext()) {n=cin.nextInt();BigInteger ans=BigInteger.valueOf(1);for(int i=1;i<=n;i++){ans=ans.multiply(BigInteger.valueOf(4*i-2));ans=ans.divide(BigInteger.valueOf(i+1));}System.out.println(ans);}}
}

五：默慈金数   默慈金数是在数学中，一个给定的数n的默慈金数是“在一个圆上的n个点间，画出彼此不相交的弦的全部方法的总数”。

六  贝尔数

Bell数，又称为贝尔数。
B(n)是包含n个元素的集合的划分方法的数目。
B(0) = 1, B(1) = 1, B(2) = 2, B(3) = 5, 
B(4) = 15, B(5) = 52, B(6) = 203,..
递推公式为，
B(0) = 1,
B(n+1) = Sum(0,n) C(n,k)B(k). n = 1,2,...
其中，Sum(0,n)表示对k从0到n求和，C(n,k) = n!/[k!(n-k)!]

七  那罗延数

N(n,k) = 1/n * C(n,k) * C(n,k-1)

八  斯特林公式

公式为：   n! \approx \sqrt{2\pi n}\, \left(\frac{n}{e}\right)^{n}.

 从图中看出，对于足够大的整数n，这两个数互为近似值。更加精确地：   

      \lim_{n \rightarrow \infty} {\frac{e^n\, n!}{n^n \sqrt{n}}} = \sqrt{2 \pi}.       或者        \lim_{n \rightarrow \infty} {\frac{n!}{\sqrt{2\pi n}\, \left(\frac{n}{e}\right)^{n}}} = 1

eg:

输入N求N的阶乘的10进制表示的长度。例如6! = 720，长度为3。

Input

第1行：一个数T，表示后面用作输入测试的数的数量。（1 <= T <= 1000)
第2 - T + 1行：每行1个数N。（1 <= N <= 10^9)

Output

共T行，输出对应的阶乘的长度。

Sample Input

3
4
5
6

Sample Output

2
3
3

判断n的长度,就是log10(n)+1，将n！代入化简就可以啦

#include<cstdio>
#include<iostream>
#include <cmath>
using namespace std;
const int MAXN = 300 + 10;
#define pi 3.1415926535898
#define e 2.718281828459
typedef long long ll;
int main()
{ll t,n,ans;scanf("%lld",&t);while(t--){scanf("%lld",&n);ans=1/2.0*log10(2*pi*n)+n*log10(n)-n*log10(e)+1;printf("%lld\n",ans);}return 0;
}

 

这篇关于几种数学公式(环排列 母函数 唯一分解定理 卡特兰数 默慈金数 贝尔数 那罗延数)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/243893。

相关文章

Python正则表达式语法及re模块中的常用函数详解

Python正则表达式语法及re模块中的常用函数详解

《Python正则表达式语法及re模块中的常用函数详解》这篇文章主要给大家介绍了关于Python正则表达式语法及re模块中常用函数的相关资料,正则表达式是一种强大的字符串处理工具,可以用于匹配、切分、... 目录概念、作用和步骤语法re模块中的常用函数总结 概念、作用和步骤概念： 本身也是一个字符串，其中
阅读更多...
JAVA保证HashMap线程安全的几种方式

JAVA保证HashMap线程安全的几种方式

《JAVA保证HashMap线程安全的几种方式》HashMap是线程不安全的,这意味着如果多个线程并发地访问和修改同一个HashMap实例,可能会导致数据不一致和其他线程安全问题,本文主要介绍了JAV... 目录1. 使用 Collections.synchronizedMap2. 使用 Concurren
阅读更多...
C++中初始化二维数组的几种常见方法

C++中初始化二维数组的几种常见方法

《C++中初始化二维数组的几种常见方法》本文详细介绍了在C++中初始化二维数组的不同方式,包括静态初始化、循环、全部为零、部分初始化、std::array和std::vector,以及std::vec... 目录1. 静态初始化2. 使用循环初始化3. 全部初始化为零4. 部分初始化5. 使用 std::a
阅读更多...
shell编程之函数与数组的使用详解

shell编程之函数与数组的使用详解

《shell编程之函数与数组的使用详解》：本文主要介绍shell编程之函数与数组的使用,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录shell函数函数的用法俩个数求和系统资源监控并报警函数函数变量的作用范围函数的参数递归函数shell数组获取数组的长度读取某下的
阅读更多...
MySQL高级查询之JOIN、子查询、窗口函数实际案例

MySQL高级查询之JOIN、子查询、窗口函数实际案例

《MySQL高级查询之JOIN、子查询、窗口函数实际案例》：本文主要介绍MySQL高级查询之JOIN、子查询、窗口函数实际案例的相关资料,JOIN用于多表关联查询,子查询用于数据筛选和过滤,窗口函... 目录前言1. JOIN（连接查询）1.1 内连接（INNER JOIN）1.2 左连接（LEFT JOI
阅读更多...
MySQL中FIND_IN_SET函数与INSTR函数用法解析

MySQL中FIND_IN_SET函数与INSTR函数用法解析

《MySQL中FIND_IN_SET函数与INSTR函数用法解析》：本文主要介绍MySQL中FIND_IN_SET函数与INSTR函数用法解析,本文通过实例代码给大家介绍的非常详细,感兴趣的朋友一... 目录一、功能定义与语法1、FIND_IN_SET函数2、INSTR函数二、本质区别对比三、实际场景案例分
阅读更多...
C++ Sort函数使用场景分析

C++ Sort函数使用场景分析

《C++Sort函数使用场景分析》sort函数是algorithm库下的一个函数,sort函数是不稳定的,即大小相同的元素在排序后相对顺序可能发生改变,如果某些场景需要保持相同元素间的相对顺序,可使... 目录C++ Sort函数详解一、sort函数调用的两种方式二、sort函数使用场景三、sort函数排序
阅读更多...
C语言函数递归实际应用举例详解

C语言函数递归实际应用举例详解

《C语言函数递归实际应用举例详解》程序调用自身的编程技巧称为递归,递归做为一种算法在程序设计语言中广泛应用,：本文主要介绍C语言函数递归实际应用举例的相关资料,文中通过代码介绍的非常详细,需要的朋... 目录前言一、递归的概念与思想二、递归的限制条件 三、递归的实际应用举例（一）求 n 的阶乘（二）顺序打印
阅读更多...
C/C++错误信息处理的常见方法及函数

C/C++错误信息处理的常见方法及函数

《C/C++错误信息处理的常见方法及函数》C/C++是两种广泛使用的编程语言,特别是在系统编程、嵌入式开发以及高性能计算领域,：本文主要介绍C/C++错误信息处理的常见方法及函数,文中通过代码介绍... 目录前言1. errno 和 perror()示例：2. strerror()示例：3. perror(
阅读更多...
CSS去除a标签的下划线的几种方法

CSS去除a标签的下划线的几种方法

《CSS去除a标签的下划线的几种方法》本文给大家分享在CSS中，去除a标签（超链接）的下划线的几种方法，本文给大家介绍的非常详细，感兴趣的朋友一起看看吧... 在 css 中，去除a标签（超链接）的下划线主要有以下几种方法：使用text-decoration属性通用选择器设置：使用a标签选择器，将tex
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2