本文主要是介绍大规模无人机集群算法flocking(蜂群),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
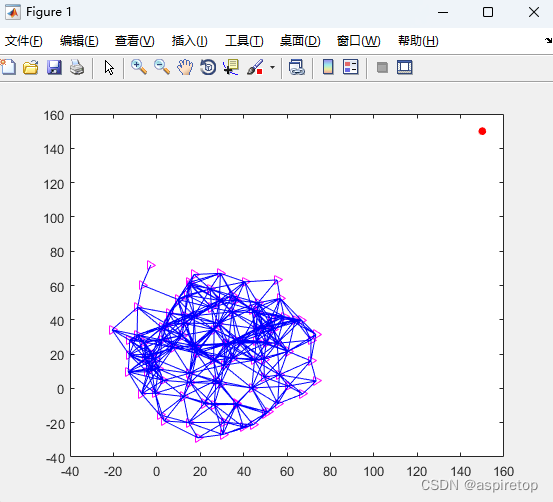
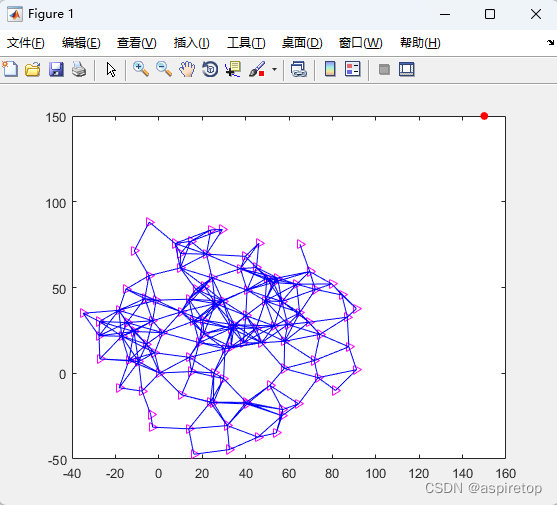
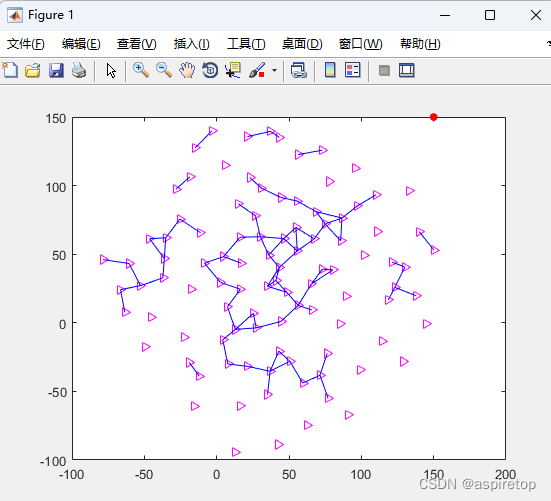
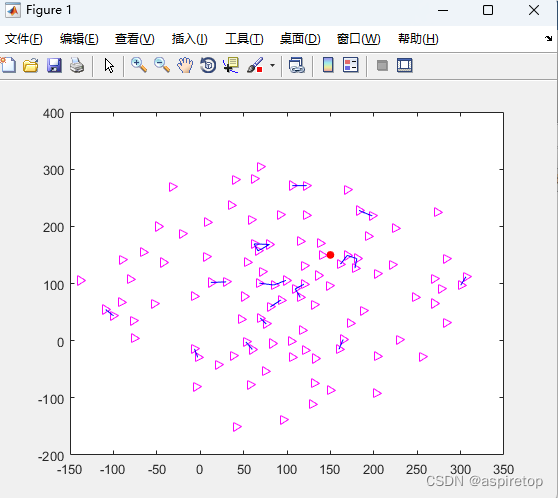
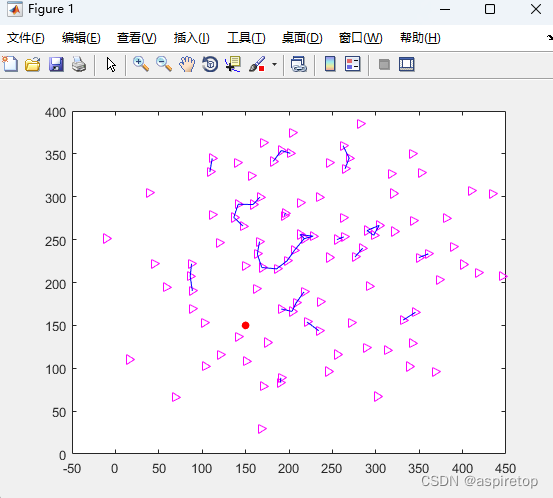

matlab2016b正常运行
这篇关于大规模无人机集群算法flocking(蜂群)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
本文主要是介绍大规模无人机集群算法flocking(蜂群),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!






matlab2016b正常运行
这篇关于大规模无人机集群算法flocking(蜂群)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
http://www.chinasem.cn/article/239631。
23002807@qq.com