TRAINING DEEP NEURAL-NETWORKS BASED ON UNRELIABLE LABELS 论文笔记

TRAINING DEEP NEURAL-NETWORKS BASED ON UNRELIABLE LABELS 论文笔记

论文摘要

本文解决的问题是如何使用不可靠的标签进行神经网络的训练。

作者通过假设一个噪声层，通过真实标签加上一个参数未知的噪声信道产生观察到的标签。

提出了一种学习神经网络参数和噪声分布的方法。

将这种方法和忽略了错误标签的标准的反向传播神经网络训练进行比较。

在几个标准的分类任务中展示了该方法对性能的改进。

证明了该方法有提升，即使标签是手动设置的正确标签，也能得到提升。

TRAINING NN WITH NOISY LABELS

首先我们要训练一个多类别分类神经网络

$p(y=i\mid x;w)$

• $x$为特征向量
• $w$为网络参数

进一步假设我们不能观察到正确的标签 $y$，我们只能获得带有噪声的标签 $z$

噪声是通过参数$\theta (i,j)=p(z=j\mid y=i)$产生的，其中噪声的分布是未知的，需要作为训练的一部分。

观察到带有噪声标签 $z$ 的几率和特征向量 $x$ 之间的关系如下：

$p(z=j\mid x;w,\theta )={\sum }_{i=1}^{k}p(z=j\mid y=i;\theta )p(y=i\mid x;w)$

• $k$为分类数

整个模型的过程如下图：

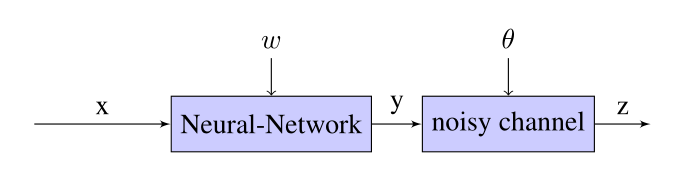
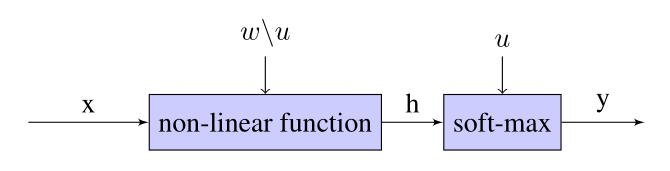
假设分类神经网络的中间层使用的是非线形层，输出层使用的是softmax分类器

input $x$ 通过非线性层 :

$h=h(x)$

通过softmax层：

$p(y=i\mid x;w)=\frac{\exp \left(u_i^{\top }h\right)}{{\sum }_{j=1}^k\exp \left(u_j^{\top }h\right)},i=1,\dots ,k$

• 其中$u_1,...,u_k$为softmax的参数，属于神经网络参数$w$的子集

在训练的过程中，给出n个特征向量，$x_1,...,x_n$，和他们对应的标签$z_1,...,z_n$ ，（$z_1,...,z_n$ 是由正确标签 $y_1,...,y_n$加上噪声得来的）

模型参数$w$的对数似然函数为：

$L(w,\theta )={\sum }_{t=1}^n\log \left({\sum }_{i=1}^{k}p\left(z_t\mid y_t=i;\theta \right)p\left(y_t=i\mid x_t;w\right)\right)$

训练的目标是：1.找到噪声 $\theta$ 的的分布。2.找到参数$w$对应的最大似然函数

因为$y_1,...,y_n$被隐藏了，使用EM算法来求解最大似然参数。

EM-auxiliary func-tion如下：

$\begin{array}{rl}Q\left(w_0,{\theta }_0,w,\theta \right)& =\sum _{t=1}^n\sum _{i=1}^{k}p\left(y_t=i\mid x_t,z_t;w_0,{\theta }_0\right)\cdot \left(\log p\left(y_t=i\mid x_t;w\right)+\log p\left(z_t\mid y_t=i;\theta \right)\right)\end{array}$

• $w_0,{\theta }_0$ 为当前的参数
• 我们要寻找参数$w, \theta $来最大化EM auxiliary function。

在更新参数的时候使用了EM算法：

EM算法分为两步，即E步和M步。

• 在E步中，根据含有噪声标签和当前参数来估计隐藏的真实数据标签。

  $\begin{array}{rl}{c}_{ti}& =p\left(y_t=i\mid x_t,z_t;w_0,{\theta }_0\right)\\ & =\frac{p\left(z_t\mid y_t=i;{\theta }_0\right)p\left(y_t=i\mid x_t;w_0\right)}{{\sum }_{j}p\left(z_t\mid y_t=j;{\theta }_0\right)p\left(y_t=j\mid x_t;w_0\right)}\\ & =\frac{{\theta }_0\left(i,z_t\right)\exp \left(u_{i0}^{\top }{h}_0\left(x_t\right)\right)}{{\sum }_j{\theta }_0\left(j,z_t\right)\exp \left(u_{j0}^{\top }{h}_0\left(x_t\right)\right)}\end{array}$

  其中$u_{10},...,u_{k0}$和$h_0(x)$是参数$w_0$的一部分。

• 在M步中，同时更新神经网络参数和噪声参数。

  θ ( i , j ) = ∑ t c t i 1 { z t = j } ∑ t c t i , i , j ∈ { 1 , … , k } \theta(i, j)=\frac{\sum_{t} c_{t i} 1_{\left\{z_{t}=j\right\}}}{\sum_{t} c_{t i}}, \quad i, j \in\{1, \ldots, k\} θ(i,j)=∑t​cti​∑t​cti​1{zt​=j}​​,i,j∈{1,…,k}

  为了找到更新后的NN参数w，我们需要最大化以下函数:

  $S(w)={\sum }_{t=1}^n{\sum }_{i=1}^k{c}_{ti}\log p\left(y_t=i\mid x_t;w\right)$

NLNN算法

input: 数据$x_1,...,x_n\in R^d$，和对应的噪声标签 $z_1, …, z_n \in (1, …, k) $

**output:**神经网络参数$w$，噪声参数$\theta$

EM算法在两个步骤之间进行迭代:

1. E-step:根据当前参数值估计真实标签

   $c_{ti}=p(y_t=i\mid x_t,z_t;w_0,{\theta }_0)$

2. M-step:更新噪声参数$\theta$

   θ ( i , j ) = ∑ t c t i 1 { z t = j } ∑ t c t i \theta(i, j)=\frac{\sum_{t} c_{t i} 1_{\left\{z_{t}=j\right\}}}{\sum_{t} c_{t i}} θ(i,j)=∑t​cti​∑t​cti​1{zt​=j}​​

训练神经网络，找到$w$使下面函数最大化：

$L(w)={\sum }_{t=1}^n{\sum }_{i=1}^k{c}_{ti}\log p\left(y_t=i\mid x_t;w\right)$

• EM算法和反向传播算法可以交替使用

• 在训练时可以先用标准方法训练神经网络，将得到参数w作为EM迭代的初始值。

• 计算训练数据上的混淆矩阵，然后用来初始噪声参数θ

  θ ( i , j ) = ∑ t 1 { z t = j } p ( y t = i ∣ x t ; w ) ∑ t p ( y t = i ∣ x t ; w ) , i , j ∈ { 1 , … , k } \theta(i, j)=\frac{\sum_{t} 1_{\left\{z_{t}=j\right\}} p\left(y_{t}=i \mid x_{t} ; w\right)}{\sum_{t} p\left(y_{t}=i \mid x_{t} ; w\right)}, \quad i, j \in\{1, \ldots, k\} θ(i,j)=∑t​p(yt​=i∣xt​;w)∑t​1{zt​=j}​p(yt​=i∣xt​;w)​,i,j∈{1,…,k}

EXPERIMENTS

作者在手写数字的MNIST数据库和TIMIT声学－音素连续语音语料库进行了测试。

第一类数据随机修改了标签，第二类数据按照概率分布修改了标签。

在MNIST数据上训练NLNN模型时，先在有噪声的数据上，使用反向传播迭代100个epoch初始化参数w，然后再使用EM算法直到收敛。在每次迭代中，用50个epoch来训练NN估计标签。在每次EM迭代中，先用随机参数进行反向传播。