时间序列预测13：用电量预测 03 ARIMA模型多步预测建模

【时间序列预测/分类】 全系列60篇由浅入深的博文汇总：传送门

接上文，本文介绍自相关模型（ARIMA）实现单变量多步输出时间序列预测任务。

自相关模型非常简单，能够实现快速、有效地对用电量进行一步或多步预测。本文主要内容如下：

• 如何创建和分析单变量时间序列数据的自相关图和部分自相关图；
• 如何使用自相关图的结果来配置一个自回归模型；
• 如何开发和评估一个自相关模型实现一周用电量预测；

如何建立多步用电量预测ARIMA模型

关于数据处理部分，请参考前一篇文章，本文会用到上文处理好的数据。

1. 自回归分析（Autocorrelation Analysis）

统计相关性总结了两个变量之间关系的强度。我们可以假设每个变量的分布符合高斯（bell曲线）分布。如果是这样，我们可以用皮尔逊相关系数来总结变量之间的相关性。皮尔逊相关系数是介于-1和1之间的数字，分别表示负相关或正相关。值为零表示没有相关性。在之前的推荐系统文章中，介绍过皮尔逊相关系数，这里再贴出公式和简单示例，方便理解。

• 皮尔逊相关系数（Pearson Correlation Coefficient）
  $$p(x,y)=\frac{\Sigma x_i{y}_i-\overline{xy}}{(n-1)s_x{s}_y}=\frac{n\Sigma x_i{y}_i-\Sigma x_i\Sigma y_i}{\sqrt{n\Sigma x_i^2-(\Sigma x_i{)}^2}\sqrt{n\Sigma y_i^2-(\Sigma y_i{)}^2}}$$

$$p(x,y)=corr(X,Y)=\frac{cov(X,Y)}{{\sigma }_x{\sigma }_y}=\frac{E[(X-{\mu }_x)(Y-{\mu }_y)]}{{\sigma }_x{\sigma }_y}$$

我们可以计算时间序列观测值与先前时间步观测值的相关性，称为滞后。因为时间序列观测值的相关性是用以前相同序列的值计算的，所以这被称为序列相关性或自相关。时间序列的滞后自相关曲线称为自相关函数（ACF）。这种图有时被称为相关图或自相关图。部分自相关函数（PACF） 是一个时间序列中的观测值与先前时间点的观测值之间关系的总结，去掉了中间观测值之间的关系。

观测值与先验时间步长的自相关由直接相关和间接相关两部分组成。这些间接相关是观测相关性的一个线性函数，在中间的时间步上进行观测。部分自相关函数试图消除的正是这些间接相关性。我们可以分别使用 plot_acf() 和 plot_pacf() 函数来绘制自相关图和部分自相关图。

为了计算和绘制自相关，必须将数据转换成单变量时间序列。下面的 to_series() 函数将把多变量数据按照一周为单位进行划分，并返回单变量时间序列。

def to_series(data):'''该函数将多变量序列转化成单变量序列'''series = [week[:, 0] for week in data]series = array(series).flatten()return series

处理思路如下：

• 1. 将数据集分割为训练集和测试集；
• 2. 从训练数据集中提取每日功耗的单变量时间序列；
• 3. 绘制ACF和PACF图， 可以通过 lags 参数指定滞后时间步骤的数量。

安装statsmodels：

pip install statsmodels

完整代码如下：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as smdef split_dataset(data):'''该函数实现以周为单位切分训练数据和测试数据'''# data为按天的耗电量统计数据，shape为(1442, 8)# 测试集取最后一年的46周（322天）数据，剩下的159周（1113天）数据为训练集，以下的切片实现此功能。train, test = data[1:-328], data[-328:-6]train = array(split(train, len(train)/7)) # 将数据划分为按周为单位的数据test = array(split(test, len(test)/7))return train, testdef to_series(data):'''该函数将多变量序列转化成单变量序列'''series = [week[:, 0] for week in data]series = np.array(series).flatten()print('series.shape:{}'.format(series.shape))return seriesdef plot_acf_pacf(series, lags):'''该函数实现绘制acf图和pacf图'''plt.figure(figsize=(16,12), dpi=150)axis = plt.subplot(2, 1, 1)sm.graphics.tsa.plot_acf(series, ax=axis, lags=lags)axis = plt.subplot(2, 1, 2)sm.graphics.tsa.plot_pacf(series, ax=axis, lags=lags)plt.tight_layout()plt.show()if __name__ == '__main__':dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, engine='c',parse_dates=['datetime'], index_col=['datetime'])lags = 365train, test = split_dataset(dataset.values)series = to_series(train)plot_acf_pacf(series, lags)

绘制的 ACF 和 PACF图如图所示：

将滞后观测的数量从365更改为50，重新绘图输出：

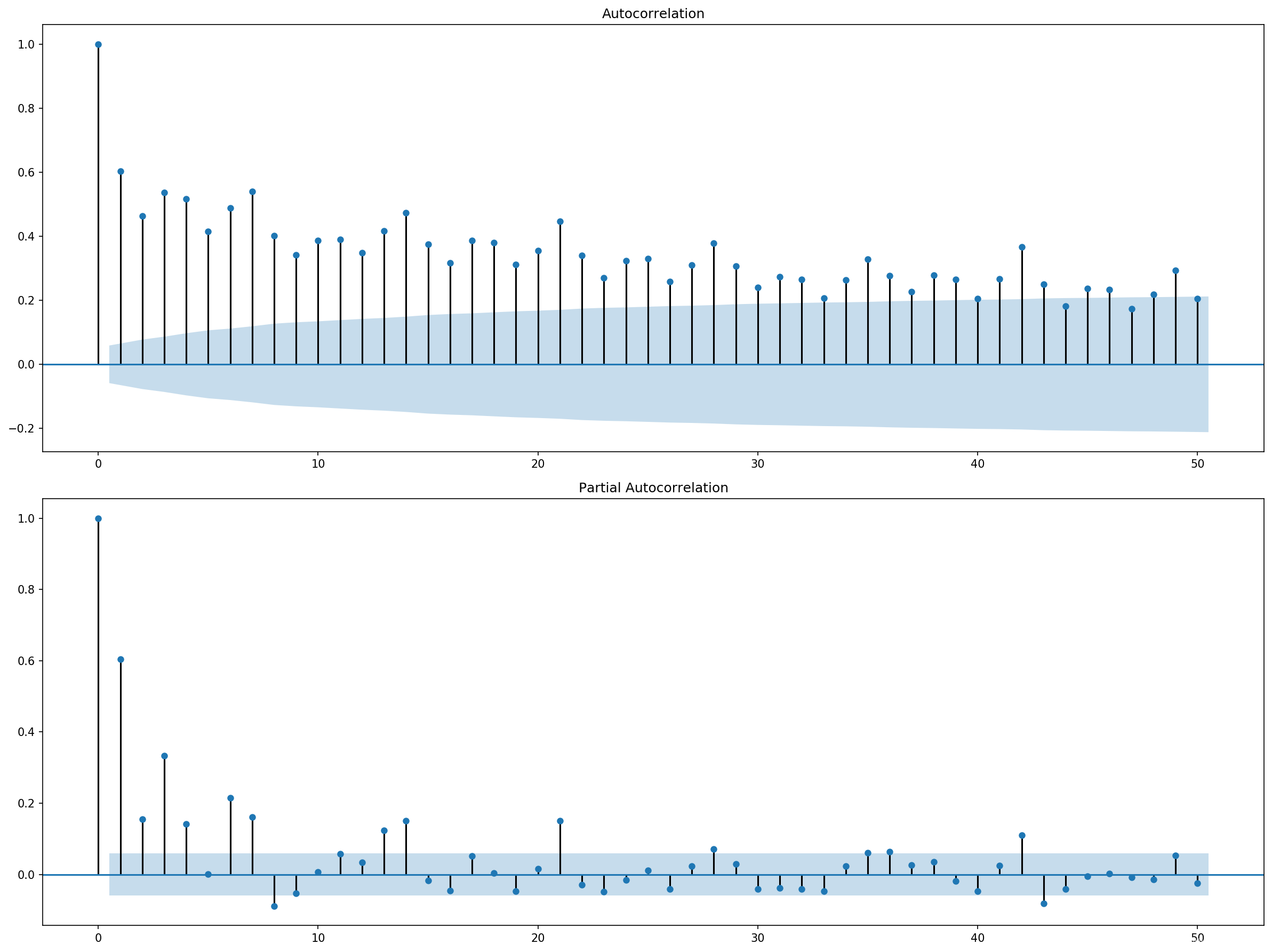
我们可以清楚地看到两个图之间的自回归模式。此模式由两个元素组成：

• ACF：大量显著的滞后观测，随着滞后的增加而缓慢退化。
• PACF：一些显著的滞后观测值，随着滞后的增加而突然下降。

ACF图表明存在一个强的自相关分量，而PACF图则表明这个分量在前7个滞后观测中是不同的。这表明一个好的开始模型是AR（7）；这是一个以7个滞后观测值作为输入的自回归模型。

2. 建立自回归模型

我们可以通过向ARIMA类的构造函数传递参数来定义ARIMA模型。经过以上分析，可以建立一个AR（7）模型，在ARIMA符号中是ARIMA（7,0,0）。

model = ARIMA(series, order=(7,0,0))

定义之后进行训练。使用默认配置，通过设置 disp=False 来禁用训练期间的所有调试信息输出。

model_fit = model.fit(disp=False)

训练完模型之后，进行训练。可以通过调用 predict() 函数并传递与训练数据相关的日期间隔或索引来进行预测。使用索引，从超出培训数据的第一个时间步开始预测，并将其再延长6天，即返回一周的预测值。

3. 完整代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
import sklearn.metrics as skm
import statsmodels.tsa as smt# 设置中文显示
plt.rcParams['font.sans-serif'] = ['Microsoft JhengHei']
plt.rcParams['axes.unicode_minus'] = Falsedef split_dataset(data):'''该函数实现以周为单位切分训练数据和测试数据'''# data为按天的耗电量统计数据，shape为(1442, 8)# 测试集取最后一年的46周（322天）数据，剩下的159周（1113天）数据为训练集，以下的切片实现此功能。train, test = data[1:-328], data[-328:-6]train = array(split(train, len(train)/7)) # 将数据划分为按周为单位的数据test = array(split(test, len(test)/7))return train, testdef evaluate_forecasts(actual, predicted):'''该函数实现根据预期值评估一个或多个周预测损失思路：统计所有单日预测的 RMSE'''scores = list()for i in range(actual.shape[1]):mse = skm.mean_squared_error(actual[:, i], predicted[:, i])rmse = math.sqrt(mse)scores.append(rmse)s = 0 # 计算总的 RMSEfor row in range(actual.shape[0]):for col in range(actual.shape[1]):s += (actual[row, col] - predicted[row, col]) ** 2score = sqrt(s / (actual.shape[0] * actual.shape[1]))print('actual.shape[0]:{}, actual.shape[1]:{}'.format(actual.shape[0], actual.shape[1]))return score, scoresdef summarize_scores(name, score, scores):s_scores = ', '.join(['%.1f' % s for s in scores])print('%s: [%.3f] %s\n' % (name, score, s_scores))def evaluate_model(model_func, train, test):'''该函数实现评估单个模型'''history = [x for x in train] # # 以周为单位的数据列表predictions = [] # 每周的前项预测值for i in range(len(test)):yhat_sequence = model_func(history) # 预测每周的耗电量predictions.append(yhat_sequence)history.append(test[i, :]) # 将测试数据中的采样值添加到history列表，以便预测下周的用电量predictions = array(predictions)score, scores = evaluate_forecasts(test[:, :, 0], predictions) # 评估一周中每天的预测损失return score, scoresdef to_series(data):'''该函数将多变量序列转化成单变量序列'''series = [week[:, 0] for week in data]series = np.array(series).flatten()print('series.shape:{}'.format(series.shape))return seriesdef arima_forecast(history):'''该函数定义ARIMA模型并进行训练和预测'''series = to_series(history)model = smt.arima_model.ARIMA(series, order=(7,0,0))model_fit = model.fit(disp=False)yhat = model_fit.predict(len(series), len(series)+6)return yhatdef model_predict_plot(dataset, days):train, test = split_dataset(dataset.values)#定义要评估的模型的名称和函数models = dict()models['arima'] = arima_forecastplt.figure(figsize=(8,6), dpi=150)for name, func in models.items():score, scores = evaluate_model(func, train, test)summarize_scores(name, score, scores)plt.plot(days, scores, marker='o', label=name)plt.grid(linestyle='--', alpha=0.5)plt.ylabel(r'$RMSE$', size=15)plt.title('ARIMA 模型预测结果',  size=18)plt.legend()plt.show()if __name__ == '__main__':dataset = pd.read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, engine='c',parse_dates=['datetime'], index_col=['datetime'])days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']model_predict_plot(dataset, days)

输出：

series.shape:(1113,)
series.shape:(1120,)
series.shape:(1127,)
series.shape:(1134,)
series.shape:(1141,)
series.shape:(1148,)
series.shape:(1155,)
series.shape:(1162,)
series.shape:(1169,)
series.shape:(1176,)
series.shape:(1183,)
series.shape:(1190,)
series.shape:(1197,)
series.shape:(1204,)
series.shape:(1211,)
series.shape:(1218,)
series.shape:(1225,)
series.shape:(1232,)
series.shape:(1239,)
series.shape:(1246,)
series.shape:(1253,)
series.shape:(1260,)
series.shape:(1267,)
series.shape:(1274,)
series.shape:(1281,)
series.shape:(1288,)
series.shape:(1295,)
series.shape:(1302,)
series.shape:(1309,)
series.shape:(1316,)
series.shape:(1323,)
series.shape:(1330,)
series.shape:(1337,)
series.shape:(1344,)
series.shape:(1351,)
series.shape:(1358,)
series.shape:(1365,)
series.shape:(1372,)
series.shape:(1379,)
series.shape:(1386,)
series.shape:(1393,)
series.shape:(1400,)
series.shape:(1407,)
series.shape:(1414,)
series.shape:(1421,)
series.shape:(1428,)
actual.shape[0]:46, actual.shape[1]:7
arima: [381.613] 393.8, 398.9, 357.0, 377.2, 393.8, 306.0, 432.2

通过输出信息可知，AR(7)模型总的RMSE大约为381千瓦。与上篇文中提到的朴素预测模型相比，该模型的表现更好，上篇文中使用一年前同一时间的观测结果预测未来一周的模型，该模型的总RMSE约为465千瓦。直观对比：

week-oya: [465.294] 550.0, 446.7, 398.6, 487.0, 459.3, 313.5, 555.1
arima   : [381.613] 393.8, 398.9, 357.0, 377.2, 393.8, 306.0, 432.2

从图中可以看出，预测下一周中前几天的用电量比之后几天的预测要容易，因为每个预测时间的误差都会增加。还可以看出，最容易预测星期五，最难预测是星期六。我们还可以看到，在350千瓦到400千瓦的中高功率范围内，需要预测的天数都具有类似的误差。

下一篇文章，介绍CNN处理时间序列预测模型。

参考：
https://www.statsmodels.org/stable/generated/statsmodels.graphics.tsaplots.plot_acf.html?highlight=plot_acf
https://www.statsmodels.org/devel/generated/statsmodels.graphics.tsaplots.plot_pacf.html
https://machinelearningmastery.com/how-to-develop-an-autoregression-forecast-model-for-household-electricity-consumption/
https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/