本文主要是介绍#Reading Paper# 【序列推荐】FiLM: Frequency improved Legendre Memory Model for Long-term Time Series Forec,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
#论文题目:【序列推荐】FiLM: Frequency improved Legendre Memory Model for Long-term Time Series Forecasting(FiLM:长期时间序列预测的频率改进勒让德记忆模型)
#论文地址:https://openreview.net/pdf?id=zTQdHSQUQWc
#论文源码开源地址:https://github.com/tianzhou2011/FiLM/
#论文所属会议:NeurIPS 2022
#论文所属单位: 阿里

一、综述
现有的序列推荐算法中,在预测长时间序列的时候,采用Transformer/LSTM等方法容易受噪声影响(因为它们倾向于过度拟合过去的所有峰值,从而导致有限的长期预测性能),LMU模型为长时间序列提供了良好的表示,同时为了减少噪声信号对勒让德投影的影响,通过结合傅立叶分析和低秩矩阵近似引入了一个降维层。更具体地说,其保留了勒让德投影的大维度表示,以确保历史数据的所有重要细节都得到保留。
二、模型结构
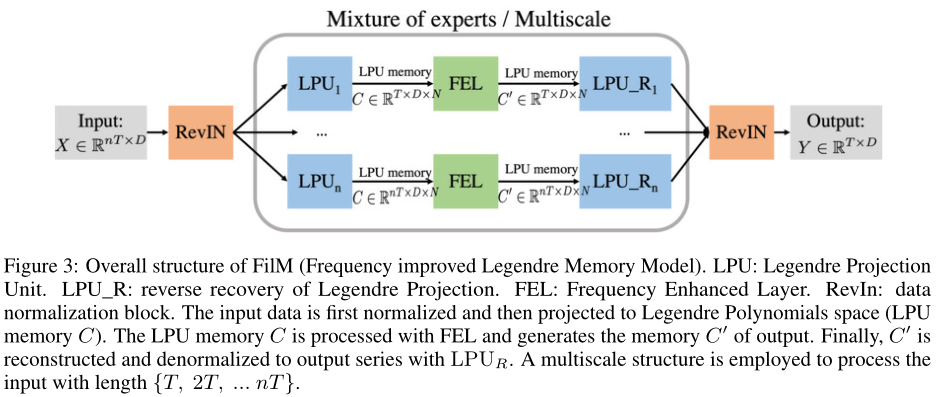
2.1 RevIN:数据标准化块
输入数据首先被归一化,然后被投影到勒让德多项式空间(LPU存储器C)。
对于每一个输入数据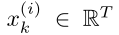 ,平均值和标准差分别为:
,平均值和标准差分别为: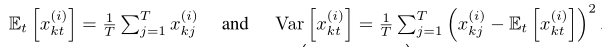 ,因此,我们可以将输入数据进行标准化,即:
,因此,我们可以将输入数据进行标准化,即:

γ \gamma γ和 β \beta β是可学习的参数矩阵,然后将标准化的输入数据发送到模型中进行后续训练。最后,我们通过归一化的倒数来反归一化模型的输出。
2.2 LPU:勒让德投影装置

LPU包括两个部分:投射和重构。
LPU是一个状态空间模型: C C Ct= A C AC ACt-1+ B B B x x xt, x x xt ∈ \in ∈|R是输入信号, C C Ct ∈ \in ∈|RN是记忆存储单元, N N N代表勒让德多项式的个数,LPU包含两个不可训练的前缀矩阵A和B,定义如下:

2.3 FEL: 频率增强层(傅里叶变换)

低秩近似:FEL具有单个可学习的权重矩阵(W∈RM′×N×N ),是我们需要从数据中学习的内容。然而,这个矩阵可能很大。因此,我们可以将W分解为三个矩阵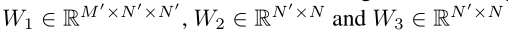 ,将勒让德多项式数设置为N = 256,分解矩阵中N′= 4。
,将勒让德多项式数设置为N = 256,分解矩阵中N′= 4。
2.4 多尺度专家机制的混合
利用具有不同时间范围的输入序列{T,2T,…nT }来预测预测层位T,并将每个专家预测与线性层合并。(因为单独的以时间T为序的模型可能缺乏一致性的对待历史序列点)。
三、总结
在长期预测中,关键的挑战是在历史信息保存和噪音降低之间进行权衡,以实现准确和稳健的预测。为了应对这一挑战,论文提出了一种频率改进的勒让德记忆模型FilM,以准确地保存历史信息并消除噪声信号。此外,论文还从理论和经验上证明了勒让德和傅立叶投影在模型中的有效性。
- FiLM模型是不同模型的拼接。主要利用勒让德投影预先处理序列信息,之后通过傅里叶变换筛选信息。同时进行不同时序信息的T变换糅合信息。
这篇关于#Reading Paper# 【序列推荐】FiLM: Frequency improved Legendre Memory Model for Long-term Time Series Forec的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







