TARJAN复习 求强连通分量、割点、桥

本文主要是介绍TARJAN复习 求强连通分量、割点、桥，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

TARJAN复习 求强连通分量、割点、桥

感觉之前写的不好， 再水一篇博客

强连通分量

“有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

​ ----百度

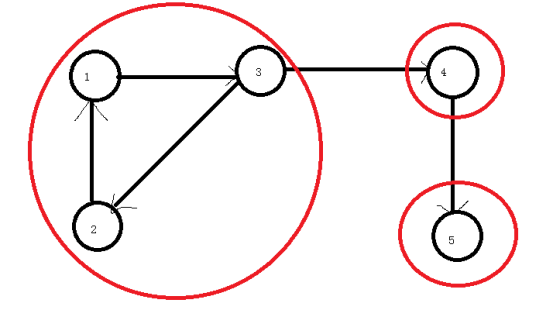
像上面的这个图就有三个强连通分量

1-2-3、4、5

设 $df{n}_i$ 记录到达点 $i$ 的时间戳

设 $lo{w}_i$ 表示 $i$ 能到达的所有点的时间戳

如果 $lo{w}_i==df{n}_i$ 就意味着 $i$ 和 $i$ 下面的点能够组成一个强连通分量，因为 $i$ 下面已经没有边可以往 $i$ 祖先方向上走了

实现的时候就用一个栈维护一下那个顺序就好了

缩点

P3387 【模板】缩点 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

看一下这个题

对于一个强连通分量来说

我们可以把它缩成一个点，并把这个点的权值设成这个强连通分量里面所有点的权值和。

然后再做 $dp$ 就好了

#include<bits/stdc++.h>
#define LL long long
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
using namespace std;
stack<int> stk;
queue<int> que;
const int N = 1e4 + 5 , M = 1e5 + 5;
LL ans , f[N] , w[N];
int hd[N] , hd2[N] , num , cnt2 , cnt , p[N] , dfn[N] , low[N] , a[N] , n , ru[N] , m , b[N] , num1;
struct E {int nt , to , fr;
}e[M << 1];
struct EE {int nt , to;
}e2[M << 1];
int read () {int val = 0 , fu = 1;char ch = getchar ();while (ch < '0' || ch > '9') {if (ch == '-') fu = -1;ch = getchar ();}while (ch >= '0' && ch <= '9') {val = val * 10 + (ch - '0');ch = getchar ();}return val * fu;
}
void add (int x , int y) {e[++cnt].to = y , e[cnt].nt = hd[x] , e[cnt].fr = x , hd[x] =cnt;
}
void dfs (int x , int fa) {dfn[x] = low[x] = ++num;stk.push(x);int y;for (int i = hd[x] ; i ; i = e[i].nt) {y = e[i].to;if (!dfn[y]) {dfs (y , x);low[x] = min (low[x] , low[y]);}else if (!p[y])low[x] = min (low[x] , dfn[y]);}if (low[x] == dfn[x]) {y = 0;num1 ++;while (y != x && !stk.empty()) {y = stk.top();stk.pop();p[y] = num1;w[num1] += a[y];}f[num1] = w[num1]; }
}
void add2 (int x , int y) { e2[++cnt2].to = y , e2[cnt2].nt = hd2[x] , hd2[x] = cnt2; }
void build () {int fa1 , fa2 , x , y;fu(i , 1 , cnt) {x = p[e[i].fr] , y = p[e[i].to];if (x == y) continue;add2 (x , y);ru[y] ++;}
}
void tuo () {fu(i , 1 , num1)if (!ru[i])que.push(i);int x , y;while (!que.empty()) {x = que.front();que.pop();for (int i = hd2[x] ; i ; i = e2[i].nt) {y = e2[i].to;ru[y] --;if (!ru[y])que.push(y);f[y] = max (f[y] , f[x] + w[y]);}}
}
int main () {int u , v;n = read () , m = read ();fu(i , 1 , n) a[i] = read ();fu(i , 1 , m) {u = read () , v = read ();add (u , v);}fu(i , 1 , n)if (!dfn[i])dfs (i , 0);build ();tuo ();fu(i , 1 , num)ans = max (ans , f[i]);printf ("%lld" , ans);return 0;
}

桥

在一个图中，如果存在一条边，把它删掉，使得整个图被分出来两个互相不连通的图，那么这条边就是桥

$dfn$ 跟求强连通分量的一样

$lo{w}_i$ 表示 $i$ 能够到达的最先被访问过的点**（不包括 $i$ 的父亲）**

设 $u,v$ ， $v$ 是 $u$ 的儿子。

如果 $lo{w}_v>df{n}_u$ 就意味着 $v$ 不能到达 $u$ 之前的点了，除非经过 $u\to v$ 这条边，所以这条边就是桥

P1656 炸铁路 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++) 
using namespace std;
const int N = 155 , M = 5005;
int n , m , hd[N] , cnt = 1 , dfn[N] , low[N] , num , ans1;
struct E {int to , nt;
} e[M << 1];
struct ANS {int u , v;
} ans[M];
bool cmp (ANS x , ANS y) { return x.u != y.u ? x.u < y.u : x.v < y.v; }
void add (int x , int y) { e[++cnt].to = y , e[cnt].nt = hd[x] , hd[x] = cnt; }
void dfs (int x , int fa) {dfn[x] = low[x] = ++num;int y;for (int i = hd[x] ; i ; i = e[i].nt) {y = e[i].to;if (y == fa) continue;if (!dfn[y]) {dfs (y , x);if (dfn[x] < low[y]) {ans[++ans1].u = min (x , y);ans[ans1].v = max (x , y);}low[x] = min (low[x] , low[y]);}elselow[x] = min (low[x] , dfn[y]);}
}
int main () {int u , v;scanf ("%d%d" , &n , &m);fu (i , 1 , m) {scanf ("%d%d" , &u , &v);add (u , v) , add (v , u);}fu (i , 1 , n) {if (!dfn[i]) dfs (i , 0);}sort (ans + 1 , ans + ans1 + 1 , cmp);fu (i , 1 , ans1) printf ("%d %d\n" , ans[i].u , ans[i].v);return 0;
}

割点

在一个图中，如果能够删掉一个点和连接这个点的所有边，使得这个图分成两个不相连的连通块，那么这个点就是割点

跟桥差不多。

因为当你找到一条桥连接 $u,v$ ，且 $u$ 是 $v$ 的父亲时，$u$ 一定是割点，因为 $v$ 连不出去了

还有一种情况就是 $u$ 是根，且 $u$ 有超过一个不同的子树，那么 $u$ 也是割点。

P3388 【模板】割点（割顶） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
using namespace std;
const int N = 2e4 + 5 , M = 2e5 + 5;
int n , m , cnt , hd[N] , dfn[N] , low[N] , num , flg[N] , ans;
struct E {int to , nt;
} e[M << 1];
void add (int x , int y) { e[++cnt].to = y , e[cnt].nt = hd[x] , hd[x] = cnt; }
void dfs (int x , int fa) {dfn[x] = low[x] = ++num;int y , sz = 0;for (int i = hd[x] ; i ; i = e[i].nt) {y = e[i].to;if (!dfn[y]) {dfs (y , x);if (dfn[x] <= low[y] && fa)flg[x] = 1;low[x] = min (low[x] , low[y]);sz ++;}elselow[x] = min (low[x] , dfn[y]);}if (!fa && sz >= 2)flg[x] = 1;if (flg[x]) ans ++;
}
int main () {int u , v;scanf ("%d%d" , &n , &m);fu (i , 1 , m) {scanf ("%d%d" , &u , &v);add (u , v) , add (v , u);}fu (i , 1 , n) {if (!dfn[i]) dfs (i , 0);}printf ("%d\n" , ans);fu (i , 1 , n)if (flg[i])printf ("%d " , i);return 0;
}

这篇关于TARJAN复习 求强连通分量、割点、桥的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---