tarjan专题

【tarjan缩点+小拓展】【POJ-2186】

用刚搞到的模板，去过了一道题差不多是个模板题有一群奶牛，奶牛A可以关注B，关注具有传递性，给出奶牛之间的关注关系，问有几只奶牛得到了所有其他奶牛的关注？互相关注的可以看成一个点，所以直接tarjan算法 + 缩点新图中，出度为0的点只能有一个，因为如果有两个，这两个新点（原连通分量）就一定是互相没有关注联系的然后答案就是这个出度为0 的新点（原连通分量）中包含的原来点的个

【hh大神的】Tarjan + 缩点模板

此模板来自 notonlysuccess 原文链接： http://www.notonlysuccess.com/index.php/tarjan/ 大神就是吊啊。不多说了，想学tarjan ，资料网上是有一堆的怎么说。。我现在理解的还不算太透彻，但用模板总行吧这里只存一下模板使用时注意清空和存图！（基于个人习惯，稍微有些小改动） #define

Tarjan的脱机最小公共祖先算法详解

Tarjan的脱机最小公共祖先算法详解一、算法概述二、算法伪代码三、C语言实现四、证明与分析在解决脱机最小公共祖先（Least Common Ancestors, LCA）问题时，Tarjan算法提供了一种高效的途径。该算法通过一次深度优先搜索（DFS）遍历整棵树，并利用并查集（Union-Find）数据结构来维护节点之间的祖先关系，从而找到任意两个节点的最小公共祖先。

poj 3352 Road Construction(边连通+tarjan+缩点)

http://poj.org/problem?id=3352 题意：简化一下原题题意，意思就是给定一个连通图，问至少要加入几条边使得整个图变成一个边连通图，即图中任意两点都有两条以上的路径（不一定直接相连）。思路：tarjan算法，设置一个low数组，在建立深搜树的过程中，我们会得到每个节点的low值，对于low值相等的节点在同一个双连通分量中。由于在同一个边连通分量中的点的“地

poj 2942 Knights of the Round Table(双连通分量+tarjan+二分图判定)

http://poj.org/problem?id=2942 题意：有N个骑士，给出某些骑士之间的仇恨关系，骑士们开会时会围坐在一个圆桌旁。一次会议能够顺利举行，要满足两个条件： 1：任意相互憎恨的两个骑士不能相邻 2：开会人数为大于2的奇数若某个骑士任何会议都不能参加，那么就必须将他踢出，给出骑士之间的仇恨关系，问最少需要踢出多少个骑士？思路：题目要求踢出的人最少，那

poj 2186 Popular Cows（tarjan + 强连通分量 + 缩点）

http://poj.org/problem?id=2186 题意：有n头牛，m个膜拜关系，膜拜关系是不可逆的而且是单向传递的，比如A膜拜B，B膜拜C,那么A也膜拜C，但B不一定膜拜A。最后问有多少头牛满足条件：除了它自己，其他所有的牛都膜拜它。思路：问题可以抽象为：给定一个有向图，n个顶点，m条有向边，有多少个顶点满足：其他所有的点都能到达该点。首先假如图G是一个有向树

poj 3694 Network（tarjan + LCA）

http://poj.org/problem?id=3694 题意：对于一个无向连通图，问加入某条边后，图中有桥的数目。思路：根据tarjan算法求出初始图的桥的数目，并用数组bridge标记桥的终点，在tarjan深搜树中求出每个节点的父节点（数组father表示）以及它们的深度，用于以后迭代求LCA。因为加入某条边后，树中就会存在环，而环中的每条边都不再是桥，这就与求LCA

强连通Tarjan算法入门

A - 迷宫城堡 Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit Status Description 为了训练小希的方向感，Gardon建立了一座大城堡，里面有N个房间(N<=10000)和M条通道(M<=100000)，每个通道都是单向的，就是说若称

强连通分量的tarjan算法

一、数据集形式其中：1595446（节点个数） 0（起始边） 1（终边）二、数据集数据集下载三、实现代码 // Tarjan.cpp : Defines the entry point for the console application.//#include "stdafx.h"#include "time.h"#include <fstream>#includ

SCC Tarjan算法

int dfs_clock,scc_cnt;int low[maxn],dfn[maxn],sccno[maxn]; //sccno[i]为i所在的SCC编号stack<int>S;vector<int>map[maxn];void tarjan( int u, int fa ){low[u] = dfn[u] = ++dfs_clock;S.push(u);for( int

csu 1526: Beam me out!（强连通分量 Tarjan）

从1开始的所有路径是否都能到达n 所用的步数是否是无限的 1）判断n是否可达 2）判断是否有环 3）判断是否所有的点都可以从1开始可达 #include <cstdio>#include <iostream>#include <cstring>#include <cmath>#include <algorithm>#include <string.h>#includ

poj 3117poj 3352 （边双连通分量+缩点 Tarjan算法）

分析：在同一个边双连通分量中，任意两点都有至少两条独立路可达，所以同一个边双连通分量里的所有点可以看做同一个点。缩点后，新图是一棵树，树的边就是原无向图的桥。现在问题转化为：在树中至少添加多少条边能使图变为双连通图。结论：添加边数=（树中度为1的节点数+1）/2 具体方法为，首先把两个最近公共祖先最远的两个叶节点之间连接一条边，这样可以把这两个点到祖先的路径上所有点收缩

强连通分量Kosaraju、Tarjan【模板】

强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量。把一个图变为一个强连通图需要添加边数：先求出原图的强连通分量，缩点后变为有向无环图，计算新图入度为0的点的个数SumIn和出度为0的点的个数SumOut

有向图的强连通算法 -- tarjan算法

（画图什么真辛苦）强连通分量：在有向图 G 中，若两个顶点相互可达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。比如上面这幅图( a, b, e ), ( d, c, h ), ( f, g ) 分

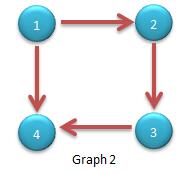
有向图强连通分量的Tarjan算法 [有向图强连通分量] 在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，

有向图强连通分量的Tarjan算法 [有向图强连通分量] 在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。下图中，子图{1,2,3,4}为一个强连通分量，因为顶点

宝石收集，tarjan

0宝石收集 - 蓝桥云课 (lanqiao.cn) n=int(input())s='0'+input()m=int(input())mp=[[] for i in range(n+1)]for i in range(m):a,b=map(int,input().split())a+=1b+=1mp[a].append(b)import syssys.setrecursionlimit

$tarjan学习$