本文主要是介绍tarjan算法介绍与分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
tarjan算法是一个求取有向图的所有强连通分量的算法,它是以算法提出者Robert Tarjan的名字来命名的。提出此算法的Robert Tarjan是普林斯顿大学的教授,同时他也是1986年的图灵奖获得者(图灵奖是计算机领域的最高荣誉,和物理、化学领域的诺贝尔奖是一个层次的奖项)。
在详细讲述该算法之前,我们需要明确几个概念(注意该算法的研究对象是有向图,无向图没有强连通等概念)。
1. 强连通
如果两个顶点可以互相通达,则称这两个顶点强连通。
2. 强连通图
如果有向图G中的任意两个顶点都是强连通的,那么我们称该有向图G是强连通图。
3. 强连通分量
非强连通图的极大强连通子图称为强连通分量。
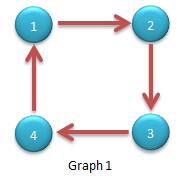
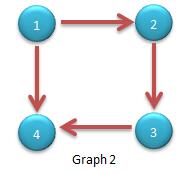
例如Graph 1就是一个强连通图,Graph 2 不是强连通图,因为4节点不存在到1、2和3的路径。
下面介绍该算法的处理流程:
1. 首先定义两个数组dfn和low,其中dfn用于记录dfs(深度优先搜索)时,当前节点u的访问时间戳,这里用计数器实现。low用于记录以当前节点u作为根节点能达到的最短时间戳,因为如果出现回边,此时的low值就可能会变小。
2. 初始化时,令节点u的dfn和low值为当前的时间戳count。
3. 如果当前节点u有相连的节点v,此时分为以下几种处理情况。
- v节点未访问过,此时直接递归处理v。递归返回时low[u]=min{low[u],low[v]}。
- v节点已访问过且v已和其它节点构成了一个连通分量,即v不在栈中,此时(u,v)为横叉边,不做任何处理。
- v节点已访问过且v在栈中,此时(u,v)是回边,low[u]=min{low[u],dfn[v]}。注意v节点由于仍在栈中,所以其low[v]的最终值还不确定,当然low[v]总是小于等于dfn[v]的,因此二者都行。
4. 当u节点的所有连接边处理完毕时,low[u]的值也就确定了。此时比较dfn[u]和low[u]的值,若二者相同,则说明栈中从该节点往上的所有节点构成一个强连通分量,将其弹出即可。要理解这个判定规则的原理,需要明确dfn和low的定义,这里dfn[u]表示节点u第一次访问时的时间戳,low[u]是u的子节点能达到的最小时间戳,若u无子节点,则low[u]等于dfn[u],即u节点自身构成一个强连通分量。
5. 需要注意的是当我们处理完一个强连通分量时,有可能需要改变搜索的起点,因此我们可以在外围添加一个循环,若某个节点未访问过,则调用1-4步骤进行处理。
以下是该算法的伪代码描述。
tarjan(u)
{dfn[u]=low[u]=++count // 为节点u设定时间戳dfn和low初值stack.push(u) // 将节点u压入栈中for each (u, v) in E // 枚举u的每一条出边if (v is not visited) // 如果节点v未被访问过tarjan(v) // 递归向下处理low[u] = min(low[u], low[v])else if (v in S) // 如果节点v还在栈内low[u] = min(low[u], dfn[v])if (dfn[u] == low[u]) // 如果节点u是强连通分量的根repeatv = stack.pop // 将v出这篇关于tarjan算法介绍与分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!