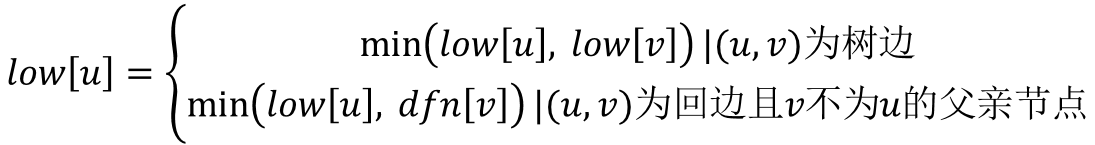割点专题
HIHO #1183 : 连通性一·割边与割点
题目链接 使用Tarjan算法计算无向图的割点和桥,提示讲解的也很清晰 需要注意的是,某一个割点可能会被多次计算,所以一般是先记录然后最后统一输出 1)按照题目的伪代码直接实现 2)稍微优化一下的,省一些空间 #include<bits/stdc++.h>using namespace std;#define cl(a,b) memset(a,b,sizeof(a))#define
P3388 【模板】割点(割顶)
~~~~~ P3388 【模板】割点(割顶) ~~~~~ 总题单链接 割点的定义 ~~~~~ 在一张无向图中,若删除一个点后连通块的数量会增加,那这个点就是割点。 怎么找割点 ~~~~~ 按 d f s dfs dfs序 访问图上的每个点,每个点只访问一遍。 ~~~~~ 先来看看时间戳的定义,若一个点的时间戳为 x x x,那
poj 1144 Network(割点)
http://poj.org/problem?id=1144 题意很简单,已知图中各边的连接情况,求割点的个数。 注意输入格式。。 #include<stdio.h>#include<vector>#include<string.h>#include<algorithm>using namespace std;vector<int> edge[110];int dfn[110]
POJ-1523 SPF 割点
题意:给你幅图,求割点 对每个点去掉后联通分量数; 裸Tarjan #include<stdio.h>#include<string.h>#include<vector>#include<queue>using namespace std;const int maxn = 1025;const int inf = 1<<29;int n,son;vector<int>
无向图的割点(关节点)
无向图的割点,也称关节点。对于无向图中不同的两点u,v,如果必须经过点w,才能构成一条从u到v的路径,那么称该w点就是割点(关节点)。关节点的求解只需要一次关于图的深度优先遍历(完成一次DFS等于生成一棵树,第一个访问的节点是根结点)。在这次DFS中,按照遍历的顺序记录每个点i的a,b表。其中,a表和b表的计算如下: a[i]=predfn ; //predfn是点的深度遍历访问顺序,在深
ZJU1311 Network - 无向图的割点
题目大意: 给出一个无向图,求图中割点的个数。(若去掉顶点i及其邻边,导致剩下的图不连通,则i是割点) 分析: 求割点有很成熟的DFS算法,照书写了一个,整理成模板备用。 /*ZJU1311 Network*/#include <stdio.h> #include <memory.h> #define clr(a) memset(a,0,sizeof(a)) #define MIN
tarjan求强连通分量+缩点+割点以及一些证明
“tarjan陪伴强联通分量 生成树完成后思路才闪光 欧拉跑过的七桥古塘 让你 心驰神往”----《膜你抄》 自从听完这首歌,我就对tarjan开始心驰神往了,不过由于之前水平不足,一直没有时间学习。这两天好不容易学会了,写篇博客,也算记录一下。 一、tarjan求强连通分量 1、什么是强连通分量? 引用来自度娘的一句话: “有向图强连通分量
【100题】第三十九题 二叉树任意两个节点间最大距离和有向图割点
一,题目(网易有道笔试) (1)求一个二叉树中任意两个节点间的最大距离,两个节点的距离的定义是这两个节点间边的个数, 比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。 (2)求一个有向连通图的割点,割点的定义是,如果除去此节点和与其相关的边,有向图不再连通,描述算法。 二,分析
A - Network POJ - 1144(割点)
链接:https://cn.vjudge.net/contest/258373#problem/A 代码: #include <iostream>#include <algorithm>#include <stdio.h>#include <string.h>#include <vector>using namespace std;char m[1000];vector<int>g
【图论】【割点】【C++算法】928. 尽量减少恶意软件的传播 II
作者推荐 视频算法专题 涉及知识点 图论 割点 LeetCode928. 尽量减少恶意软件的传播 II 给定一个由 n 个节点组成的网络,用 n x n 个邻接矩阵 graph 表示。在节点网络中,只有当 graph[i][j] = 1 时,节点 i 能够直接连接到另一个节点 j。 一些节点 initial 最初被恶意软件感染。只要两个节点直接连接,且其中至少一个节点受到恶意软件的感染,
图的连通性相关总结:强连通,双连通,割点割边,2-sat
刚学完了连通性相关的知识,总结一下 以下均使用tarjan算法 强联通分量 定义 强连通分量即强联通子图,一般我们都在有向图中求取最大强连通分量,即有向图一张图中任两点可达的最大子图。其中单独一个点也是强联通子图。 算法 在这里我们使用tarjan算法,维护两个栈,系统堆栈(递归隐式使用),连通子图堆栈。维护两个数组,dfn时间戳数组和low最早可达(自己取的名字)数组。 算法过程如下
无向连通图的割点、桥
无向连通图的割点、桥 泳裤王子原创,转载请注明出处 http://blog.csdn.net/tclh123/article/details/6705392 预备知识: 割点集合 在一个无向连通图中,如果有一个顶点集合,删除这个顶点集合,以及这个集合中所有顶点相关联的边以后,原图变成多个连通块,就称这个点集为割点集合。 割边集合 在一个无向连通
【图论】 【割点】 【双连通分类】LCP 54. 夺回据点
本文涉及知识点 图论 割点 双连通分类 割点原理及封装好的割点类 LeetCode LCP 54. 夺回据点 魔物了占领若干据点,这些据点被若干条道路相连接,roads[i] = [x, y] 表示编号 x、y 的两个据点通过一条道路连接。 现在勇者要将按照以下原则将这些据点逐一夺回: 在开始的时候,勇者可以花费资源先夺回一些据点,初始夺回第 j 个据点所需消耗的资源数量为 cost[j]
tarjan算法——求无向图的割点和桥
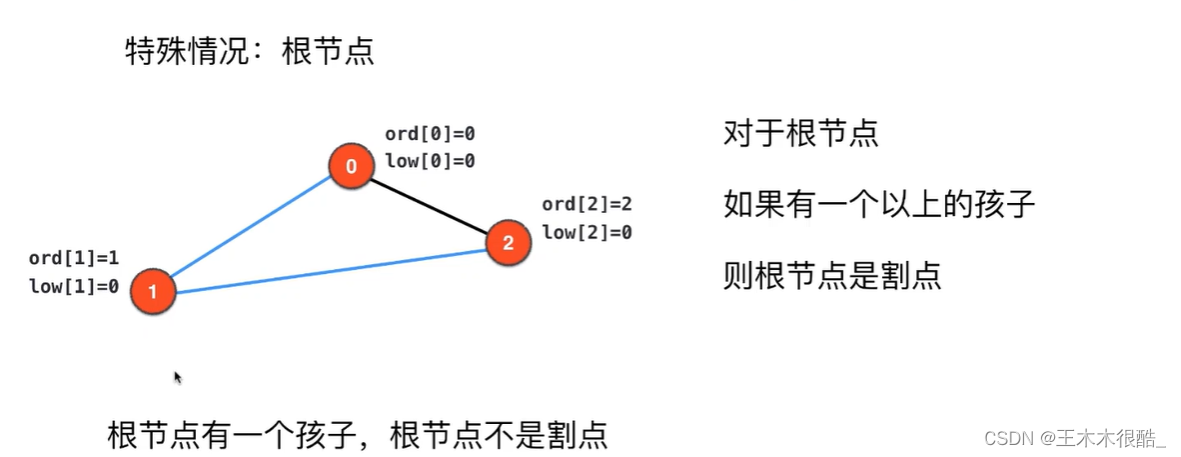
一.基本概念 1.桥:是存在于无向图中的这样的一条边,如果去掉这一条边,那么整张无向图会分为两部分,这样的一条边称为桥无向连通图中,如果删除某边后,图变成不连通,则称该边为桥。 2.割点:无向连通图中,如果删除某点后,图变成不连通,则称该点为割点。 二:tarjan算法在求桥和割点中的应用 1.割点: 1)当前节点为树根的时候,条件是“要有多余一棵子树”(如果这有一颗子树,去掉这
【树上倍增】【割点】 【换根法】3067. 在带权树网络中统计可连接服务器对数目
作者推荐 视频算法专题 本文涉及知识点 树上倍增 树 图论 并集查找 换根法 深度优先 割点原理及封装好的割点类(预计2024年3月11号左右发布) LeetCode3067. 在带权树网络中统计可连接服务器对数目 给你一棵无根带权树,树中总共有 n 个节点,分别表示 n 个服务器,服务器从 0 到 n - 1 编号。同时给你一个数组 edges ,其中 edges[i] = [ai,
【分类讨论】【割点】1568. 使陆地分离的最少天数
作者推荐 动态规划的时间复杂度优化 本文涉及知识点 分类讨论 割点 LeetCode1568. 使陆地分离的最少天数 给你一个大小为 m x n ,由若干 0 和 1 组成的二维网格 grid ,其中 1 表示陆地, 0 表示水。岛屿 由水平方向或竖直方向上相邻的 1 (陆地)连接形成。 如果 恰好只有一座岛屿 ,则认为陆地是 连通的 ;否则,陆地就是 分离的 。 一天内,可以将 任何单
Hihocoder#1183 : 连通性一·割边与割点(连通图求割点和割边)
时间限制: 10000ms 单点时限: 1000ms 内存限制: 256MB 描述 还记得上次小Hi和小Ho学校被黑客攻击的事情么,那一次攻击最后造成了学校网络数据的丢失。为了避免再次出现这样的情况,学校决定对校园网络进行重新设计。 学校现在一共拥有N台服务器(编号1..N)以及M条连接,保证了任意两台服务器之间都能够通过连接直接或者间接的数据通讯。 当发生黑客攻击时
POJ 1144 Network【割点】
题目: A Telephone Line Company (TLC) is establishing a new telephone cable network. They are connecting several places numbered by integers from 1 to N. No two places have the same number. The lines a
桥和割点,以及图的遍历树
目录 什么是桥 寻找桥的算法 代码实现 什么是割点 寻找割点的算法 代码实现 什么是桥 寻找桥的算法 代码实现 import java.util.ArrayList;public class FindBridges {private Graph G;private boolean[] visited;private int
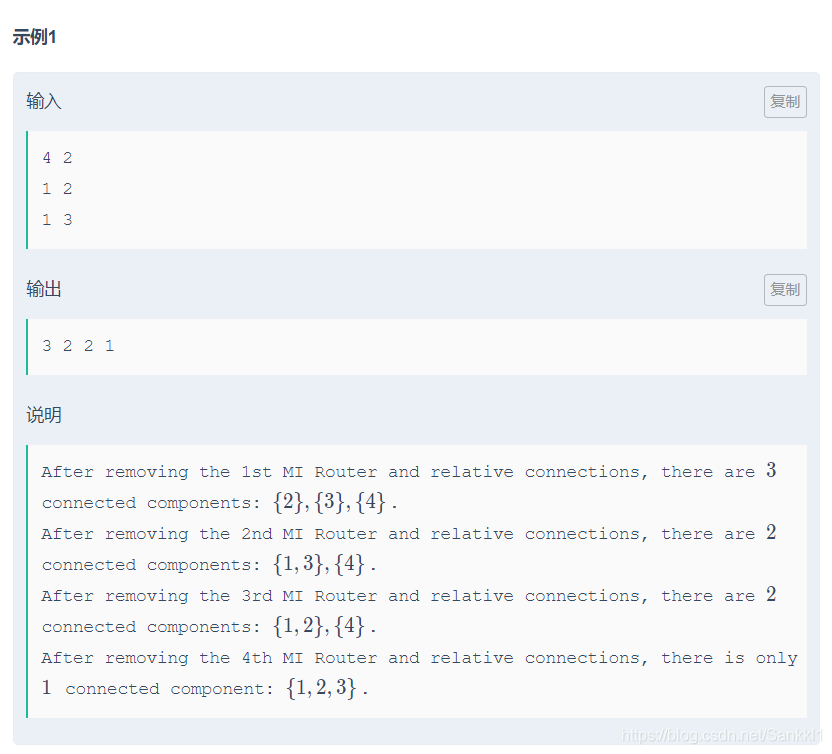
2020ICPC·小米 网络选拔赛第一场 D.Router Mesh(tarjan 割点)
题目链接:https://ac.nowcoder.com/acm/contest/7501/D tarjan的割点算法可以参考博文:https://blog.csdn.net/csyifanZhang/article/details/105370924 分析 求一个图去掉第 i 个点后的连通块数量 分析 对于每个点,首先总共有 sum 个连通块,求出每个点所在的强连通分量的个数