本文主要是介绍关于蛙跳算法的计算机文献,进化策略自主选择的改进混洗蛙跳算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
混洗蛙跳算法[(shuffled frog leaping algorithm, SFLA),以其模型简单,寻优速度快等优点得到学者的广泛关注。Elbeltagi等[通过实验表明SFLA在求解某些连续和离散优化问题时的成功率和寻优速度优于遗传算法、模因算法和蚁群算法;Babak等[利用SFLA改进K均值聚类方法,实验结果表明其优于遗传算法、模拟退火算法、蚁群算法等聚类算法。目前SFLA已应用到经济负荷分配[、多目标优化[、优化调度[、信号重构[和故障诊断[等问题。同时,针对SFLA的不足,许多学者在种群多样化[、进化方式改进
1 进化策略自主选择的改进混洗蛙跳算法
整个群体的当前最优解仅是算法迭代过程中某个个体自身所能找到的最优位置,只能代表所有个体的目前最好水平,而不能代表目前的整体进化水平。特别是在求解高维复杂的优化问题时,当前最优解很可能是一个局部极值,仅利用这一个局部极值来指导整个群体的学习,易陷入局部最优,较难达到所要的求解效果。进化论研究表明:生物对环境有巨大的适应能力,环境的变化会引起生物的变化,生物会由此改进其行为,环境的多样化是生物多样化的根本原因,而混洗蛙跳算法个体更新所面临的环境就是其他个体传递给它的知识,个体参照的知识不同则进化行为也应有所不同,即个体的进化策略在整个进化过程中不应该是一成不变的。分析青蛙个体在整个进化过程中,能够获得知识的来源主要分为4部分:1)分组内最优个体的知识;2)当前种群最优个体的知识;3)进化过程中的群体知识;4)进化过程中其他个体的知识。本文针对这4类知识提出4种策略行为来完成个体进化。
1.1 最差个体的4种进化策略
1) 基于分组内和种群内最优个体学习的进化策略。
经典SFLA的最差个体先是参照组内最优个体进行更新,如果新个体的适应值没有提高再参照种群最优个体,这种进化方式在迭代初期具有寻优缓慢的缺点,不利于种群间的信息共享。本文提出基于分组内和种群内最优个体学习的进化策略:
$
\left\{\begin{array}{l}{S_{i, t+1}=\operatorname{rand}( ) \times\left(x_{\mathrm{b}, t}-x_{\mathrm{w}, t}\right)+\mathrm{rand}( ) \times\left(x_{\mathrm{g}, t}-x_{\mathrm{w}, t}\right)} \\ {x_{\mathrm{w}, t}=\omega x_{\mathrm{w}, t}+S_{i, t+1}}\end{array}\right.
$
(1)
2) 基于进化过程中的群体知识学习的进化策略。
社会中的个体通常具有趋同性,即个体的行为容易受到群体共知所影响,即群体知识。群体知识可以用“群体位置质心”来代替,为方便计算采用所有个体位置的均值作为质心:
$
\left\{\begin{array}{l}{S_{i, t+1}=\operatorname{rand}( ) \times\left(\frac{\sum\limits_{i=1}^{N} x_{i, t}}{N}-x_{w, t}\right)} \\ {x_{\mathrm{w}, t}=\omega x_{\mathrm{w}, t}+S_{i, t+1}}\end{array}\right.
$
(2)
式中N为种群的个数,式(1)和(2)引入权重ω,用来描述父代个体对子代个体的影响。ω值较大全局寻优能力强,反之则局部寻优能力强。当求解问题空间较大时,为了在搜索速度和搜索精度之间达到平衡,常用的做法是使算法在前期具有较高的全局搜索能力,而在后期具有较高的局部搜索能力以提高收敛精度,文中按照递减方式进行赋值:
$
\omega=\omega_{\max }-\sin \left(\frac{t}{T} \times \frac{{\rm{ \mathsf{ π} }}}{2}\right) \times\left(\omega_{\max }-\omega_{\min }\right)
$
(3)
式中:t为当前迭代次数;T为最大迭代次数;ωmin和ωmax分别为ω的最小值和最大值,文中取ωmin=0.2,ωmax=0.9。
3) 基于种群内最优个体和其他个体知识学习的进化策略。
当一个分组内的个体适应值相差不大的时候,再采用分组内的最优个体来指导更新最差个体对提升寻优性能的效果并不明显(可能已陷入分组内最优),此时需要引入其他分组的个体来帮助该分组提升寻优效果。同时为提升寻优速度,要参照种群内最优个体的知识。更新的最差个体为:
$
\left\{\begin{array}{l}{S_{i, t+1}=\operatorname{rand}( ) \times\left(x_{r 1, t}-x_{r 2, t}\right)} \\ {x_{w, t}=x_{g, t}+S_{i, t+1}}\end{array}\right.
$
(4)
式中r1和r2是来自于其他分组的个体,且互不相同。
4) 基于其他个体知识学习的进化策略。
当种群内的个体适应度相差不大的时候,此时或已寻找到最优解或是陷入局部最优解,此时需要随机参考不同的个体来指导进化。这种随机选取个体进行进化的方式等价于个体变异,并且这种变异方式与一些基于混沌理论进行变异方式相比较,更具有目的性和方向性。
$
\left\{\begin{array}{l}{S_{i, t+1}=\operatorname{rand}( ) \times\left(x_{r 2, t}-x_{r 3, t}\right)} \\ {x_{w, t}=x_{r 1, t}+S_{i, t+1}}\end{array}\right.
$
(5)
1.2 计算进化策略立即价值
立即价值是指采用某种策略行为后,所产生的适应值f(xi, new, t+1)较上一次迭代计算的适应度f(xi, t)的提高程度:
$
v_{i}(t)=\frac{f\left(x_{i}, t\right)-\min \left(f\left(x_{i}, t\right), f\left(x_{i, \text { new }}, t+1\right)\right)}{f\left(x_{i}, t\right)}
$
(6)
若某一策略收益计算如果为零,说明该策略本次迭代没有取得很好的寻优效果,但这只是瞬时效益,不能代表此种进化策略不好,故还需计算其未来价值。
1.3 计算进化策略未来价值
个体在没有任何先验知识的前提下,在每次确定所要采取何种策略的行为时,可通过对已获得知识的利用和对新知识的探索间进行协调来确定,以便更快捷的做出最优决策。信心上界(upper confidence bound, UCB)算法
$
s_{i}(t)=\alpha\left(\frac{N_{i, \mathrm{p}}(t)}{M_{i, \mathrm{p}}(t)}+\sqrt{\frac{C_{0} \times \lg (t)}{N_{i, \mathrm{p}}(t)}}\right)+\\
\qquad
(1-\alpha)\left(\frac{N_{i, {\rm g}}(t)}{M_{i, {\rm g}}(t)}+\sqrt{\frac{C_{0} \times \lg (N \times t)}{\sum\limits_{i=1}^{N} N_{i, {\rm p}}} )}\right.
$
(7)
式中:si(t)为进化策略未来价值;t是当前迭代的次数;α和C0是一个常数,α的作用是平衡个体未来价值与全局未来价值在进化策略预测的重要性;C0的作用是平衡个体所获得知识的利用和探索需求。文中按照UCB算法的取值C0=2。令Ni, p(t)为个体在第t次迭代之前采用第i种策略的成功次数;Mi, p(t)为个体在第t次迭代之前采用第i种策略总的执行次数;Ni, g(t)为所有个体在第t次迭代之前采用第i种策略的成功个数;Mi, g(t)为所有个体在第t次迭代之前采用第i种策略总的执行次数,分2种情况按照UCB公式来计算未来价值,一种是单个个体执行某一策略的成功率,另一种是该策略在整个种群的成功率;N是种群规模。
1.4 计算进化策略综合奖励
在考察一种策略是否有效,需考虑实施该策略的立即价值、估算的未来价值,同时还要考虑之前的历史经验Pi(t),即上一次迭代采用该策略的概率,故计算个体采用某种策略所能获得的综合奖励。
$
v_{s i}(t)=v_{i}(t)+s_{i}(t)+P_{i}(t), 1 \leqslant i < M
$
(8)
式中M为多策略行为的个数。
1.5 更新进化策略选择概率
每个个体在分别计算完采用M种策略行为的综合奖励后,更新在第t+1次进化过程中采用某种进化策略的概率用以指示将要采用何种进化策略:
$
P_{i}(t+1)=P_{\min }+\frac{v_{\mathrm{si}}(t)}{\sum\limits_{i=1}^{N} v_{\mathrm{s} i}(t)}\left(1-M P_{\min }\right)
$
(9)
为保证某种策略都会存在概率不为0的情况,需要设置一个最小概率Pmin < 1/M。
1.6 个体进化策略概率变异算法
在算法的进化过程中会存在个体一直采取某种策略行为,虽然每次进化都会对个体适应值有所提升,但提升幅度不大,有可能造成个体寻优速度缓慢或造成陷入局部最优的情况,所以需要对这种情况进行判断来降低当前所采取策略行为的选择概率。适应度方差可以反映粒子的收敛程度,方差越小说明已陷入局部最优或已发现全局最优解,故算法采用个体适应值的方差来判断:
$
\sigma^{2}=\frac{\sum\limits_{i=t-t_{n}}^{t}\left(f_{i}-\overline{f}\right)^{2}}{t_{n}}
$
(10)
式中:t代表当前的迭代次数;tn为第t次迭代前的适应值个数(本文取10);fi为每次迭代的适应值;f为tn个适应值的均值,如果σ2小于某一阈值则将该策略行为的概率置为Pmin。
2 数值实验及分析
选取与文中ESAS_SFLA算法4种策略相关且具有代表性的算法进行比较。将其与基本混洗蛙跳算法[(SFLA)、差分进化算法(DE/best/1、DE/rand/1)[、基本粒子群算法(PSO)[、(MSFLA)[、(MSFLA1)[、(ISFLA)[和(MSFLA2)[进行寻优性能对比。这里选用PSO和DE进行对比,是由于其进化方式与本文的某种进化策略相似。实验环境为:Windows7操作系统,Intel酷睿i5处理器,主频2.5 Hz,4G内存,开发工具为Matlab R2014a。针对10个函数极值求解问题,各算法的参数设置如下:种群个数均设置为N=100;各自迭代500次,每个算法独立运行10次;PSO的ω=0.729 8, c1=1.496 2, c2=1.496 2;DE/rand/1、DE/best/1的F=0.5, CR=0.3;ESAS_SFLA、SFLA、MSFLA、MSFLA1、MSFLA2和ISFLA的分组个数为10,子群内个体数为10,且ESAS_SFLA的参数α=0.5,MSFLA、MSFLA1、MSFLA2和ISFLA的其他参数参照相应文献。测试函数如
表 1
(Table 1)
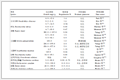
表 1 优化测试函数
Table 1 Optimization test functions
序号
测试函数
搜索空间
最优解
1
$f_{1}=\sum\limits_{i=1}^{n} x_{i}^{2}$
[-100, 100]n
0
2
$f_{2}=\sum\limits_{i=1}^{n}\left|x_{i}\right|+\prod\limits_{i=1}^{n}\left|x_{i}\right|$
[-10, 10]n
0
3
$f_{3}=\sum\limits_{i=1}^{n}\left(\sum\limits_{j=1}^{i} x_{j}\right)$
[-100, 100]n
0
4
f4=max(abs(xi)
[-100, 100]n
0
5
$\begin{aligned} f_{5}=& \sum\limits_{i=1}^{n-1}\left[100 \times\left(x_{i+1}-x_{i}^{2}\right)^{2}+\right.\\ &\left(x_{i}-1\right)^{2} ] \end{aligned}$
[-30, 30]n
0
6
$f_{6}=\sum\limits_{i=1}^{n} i x_{i}^{4}+\operatorname{rand}(0, 1)$
[-1.28, 1.28]n
0
7
$f_{7}=\sum\limits_{i=1}^{n}\left[x_{i}^{2}-10 \cos \left(2 {\rm{ \mathsf{ π} }} x_{i}\right)\right]+10 n$
[-5.12, 5.12]n
0
8
$\begin{array}{c}{f_{8}=20+\exp (1)-20 \exp } \\ {\left[-\frac{1}{5} \sqrt{\frac{1}{n} \sum\limits_{i=1}^{n} | x_{i}^{2}}\right]-} \\ {\exp \left[\frac{1}{n} \sum\limits_{i=1}^{n} \cos \left(2 {\rm{ \mathsf{ π} }} x_{i}\right)\right]}\end{array}$
[-32, 32]n
0
9
$f_{9}=\frac{1}{4 \;000} \sum\limits_{i=1}^{n} x_{i}^{2}-\prod\limits_{i=1}^{n} \cos \left[\frac{x_{\mathrm{i}}}{\sqrt{i}}\right]+1$
[-600, 600]n
0
10
$\begin{array}{c}{f_{10}=\frac{{\rm{ \mathsf{ π} }}}{n}\left\{10 \sin \left({\rm{ \mathsf{ π} }} y_{1}\right)+\right.} \\ {\sum\limits_{i=1}^{n-1}\left(y_{\mathrm{i}}-1\right)^{2}[1+} \\ {\quad 10 \sin ^{2}\left({\rm{ \mathsf{ π} }} y_{\mathrm{i}+1}\right) ]+} \\ {\left(y_{\mathrm{n}}-1\right)^{2} \}+\sum\limits_{i=1}^{n} u\left(x_{i}\right.}, \\ {10, 1 \;000, 4 )}\end{array}$
其中u(xi, a, k, m)=
$\left\{\begin{array}{l}{k\left(_{i}^{x}-a\right)^{m}, x_{i}>a} \\ {0, -a \leqslant x_{i}
$y_{i}=1+\frac{x_{i}+1}{4}$
[-50, 50]n
0
表 1 优化测试函数
Table 1 Optimization test functions
从最优结果、最差结果、平均结果和方差可以看出,ESAE_SFLA寻优结果最好。从不同维数的实验结果可知本文算法具有很好的稳定性,即在增加维数的情况下寻优效果变化不大,都可以获得较为理想的解。虽然在函数f8的f10的测试结果中可知ESAE_SFLA和MSFLA2的最优结果相似,但从收敛曲线对比结果可知ESAE_SFLA所需的迭代次数更少。本文算法的性能随维数的增加没有明显的改变。主要因为ESAE_SFLA每个分组的最差个体都会在进化过程中不断吸取各类知识,并将其转换为指导自己采用不同寻优行为的进化策略,算法可以充分利用每步迭代获得的立即价值、估算的未来价值和历史经验来判断如何从其他个体汲取有用的知识,可以让算法在自身感知的情况下选用较优的进化策略,同时个体进化策略概率变异算法可以根据历史最优值的方差来调整进化策略,进而解决了算法在求解某些复杂函数时收敛速度慢、容易陷入局部最优的缺点,有利于获得全局最优解。
为对比本文算法在高维函数寻优的性能,选取100维函数测试平均最优适应值收敛曲线如f1~f4的迭代曲线可以看出,其他算法由于采用固定的进化策略和单一的知识来源,使得寻优能力在达到一定精度后再难跳出局部最优,而在ESAE_SFLA的f1~f4的迭代曲线可以看出即使维数达到100,算法仍能较快的迭代方式不断更新最优解;而从f7~f9的迭代曲线可以看出ESAE_SFLA和MSFLA2的寻优效果差不多,但也可以看出文中算法可用较少的迭代次数获取较优结果;同时由f5、f6和f10的收敛曲线可知,ESAE_SFLA在迭代后期寻优性能不如函数f1~f4明显,这也从侧面说明了“没有免费午餐定理”,但从实验结果来看,文中算法相对于其他比较算法而言还是具有很好的优化性能。从对比数据和收敛曲线可知,ESAE_SFLA在处理高维函数过程中具有较好的适应性。同时从图中可以看出,虽然文中实例的迭代次数都是500次,但ESAE_SFLA在迭代次数300次以内就以获得较好的寻优结果,这表明计算的综合奖励可以有效的增强个体寻优性能,避免了一些局部震荡计算,这种寻优特性尤其适合适应度计算量复杂的优化问题,即以更少的迭代次数获取更优的结果,换言之就是当计算适应度函数值的时间复杂度越大于ESAE_SFLA计算综合奖励的复杂度时,就越能体现ESAE_SFLA算法计算能力的优越性。
图 1
图 1 f1~f10平均适应值收敛曲线
Fig. 1 Average fitness convergence curves of Function f1~f10
4 结论
1) 算法中所提的个体进化策略自主选择方法,有利于最差个体在进化过程中选择不同的知识来指导进化行为,并采用贪心算法的方式使得个体在每次迭代都可以获得较好的寻优结果。算法具有较好地平衡全局探索能力和局部挖掘能力,从而增加了算法的求解速度和精度。
2) 个体在迭代过程中可以利用所获得的知识采用不同的进化策略,将个体赋予一定的智能自主性,减小了由于单一进化策略造成陷入局部最优解的几率。
3) 基于高维测试函数的测试结果表明,所提算法在整体上具有较好的全局寻优能力且收敛速度较快,可以在较少的迭代次数内获得较为满意的寻优结果,适合于求解一些适应度计算复杂和耗时的优化问题。
本文所提的算法对于其他进化算法的改进具有一定的借鉴意义,同时个体进化策略的选择还有一定的研究空间。
这篇关于关于蛙跳算法的计算机文献,进化策略自主选择的改进混洗蛙跳算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






