本文主要是介绍估算总体标准差sigma = s/c4,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
sigma = s / c4 是一种用于估算总体标准差(sigma)的简单方法,其中:
- s 是各组样本标准差的均值。
- c4 是一个与样本容量相关的常数,通常根据样本容量的大小选择合适的值。
这个方法通常用于质量控制和过程监控,尤其在使用 X-S 控制图时。通过计算各组样本标准差的均值并除以适当的 c4 值,可以估算总体标准差,以便在质量控制中对过程的变异性进行评估和监控。请确保所使用的 c4 值与样本容量相符,以获得准确的估算结果。
-
当使用 sigma = s / c4 这种估算总体标准差的方法时,有一些要点需要深入了解:
-
样本标准差 (s): 这是每组样本的标准差,通常是用来度量每组数据集内部的离散程度。它可以通过统计工具或软件计算得出,确保使用适当的自由度(通常为 ddof=1)以进行Bessel修正。
-
常数 c4: c4 是一个与样本容量(每组的数据点数量)相关的常数。它的值通常可以在统计文献或表格中找到,或者根据特定的样本容量计算。不同的样本容量对应不同的 c4 值,所以您需要确保选择正确的 c4 值,以使估算尽可能准确。
-
适用性: 这种方法通常适用于样本容量较大的情况,特别是在质量控制和过程监控中,用于估算总体标准差。对于小样本容量或非正态分布的情况,这种方法可能不够准确。
-
质量控制应用: 通常,在质量控制中,使用 X-S 控制图,其中 X 图显示了每组样本的均值,而 S 图显示了每组样本的标准差。使用 sigma = s / c4 估算总体标准差有助于监控过程的变异性,并检测异常情况。
-
准确性与误差: 请注意,这种估算方法是一种近似估算,可能存在一定的误差。准确性取决于样本的大小、样本容量和数据的分布。在实际应用中,应根据需要的精度和置信度来选择适当的估算方法。
总之,sigma = s / c4 是一种简单但有用的方法,可用于估算总体标准差,特别在质量控制和过程监控中。确保了解常数 c4 的选择和适用性,以便在合适的情况下使用这个估算方法。
-
import numpy as np# 准备数据,每组数据是一个NumPy数组
data = [np.array([28.1, 29.5, 30.2, 31.3, 30.5, 29.8, 30.2, 31.0, 28.9, 30.3]),np.array([27.8, 28.9, 29.7, 28.5, 30.0, 29.2, 29.4, 28.8, 29.6, 29.1]),np.array([30.2, 29.8, 31.1, 30.5, 29.9, 30.7, 30.3, 29.6, 30.0, 30.5]),np.array([29.0, 28.7, 29.4, 28.9, 29.3, 28.8, 29.2, 28.6, 29.1, 29.4]),np.array([31.5, 30.7, 31.0, 30.2, 30.9, 31.3, 30.8, 31.1, 30.6, 30.4])
]# 计算各组样本标准差
group_std = [np.std(group, ddof=1) for group in data]# 计算各组样本标准差的均值
average_group_std = np.mean(group_std)# 将data数据扁平化成一个NumPy数组
flat_data = np.concatenate(data)
# 计算整体数据集扁平化样本标准差
# population_std = np.std(data,ddof=1)
population_std = np.std(flat_data, ddof=1) # 使用Bessel修正# 选择适当的 c4 值(与样本容量有关)
sample_size = len(data[0]) # 假设所有组的样本容量相同
# 根据样本容量选择 c4 值
c4_values = {2: 0.7979,3: 0.8862,4: 0.9213,5: 0.9400,6: 0.9515,7: 0.9594,8: 0.9650,9: 0.9693,10: 0.9727,
}
c4 = c4_values.get(sample_size, None)
print("sample_size样本容量: ", sample_size)
print("根据样本容量选择 c4 值: ",c4)if c4 is None:print("请提供适当的 c4 值或扩展字典以包括所需的样本容量。")
else:# 步骤5:使用公式 sigma = (average_group_std) / c4 估算总体标准差estimated_population_std = average_group_std / c4print("各组样本标准差的均值 (s):", average_group_std)print("估算的总体标准差 (sigma):", estimated_population_std)# 计算整体数据扁平化集样本标准差 population_std = np.std(data,ddof=1)
print("计算整体数据集(扁平化)样本标准差: ",population_std,np.std(data,ddof=1))# sample_size样本容量: 10
# 根据样本容量选择 c4 值: 0.9727
# 各组样本标准差的均值 (s): 0.5474311211038614
# 估算的总体标准差 (sigma): 0.5627954365208815
# 计算整体数据集(扁平化)样本标准差: 0.9033294424697188 0.9033294424697188
# [Finished in 1.3s]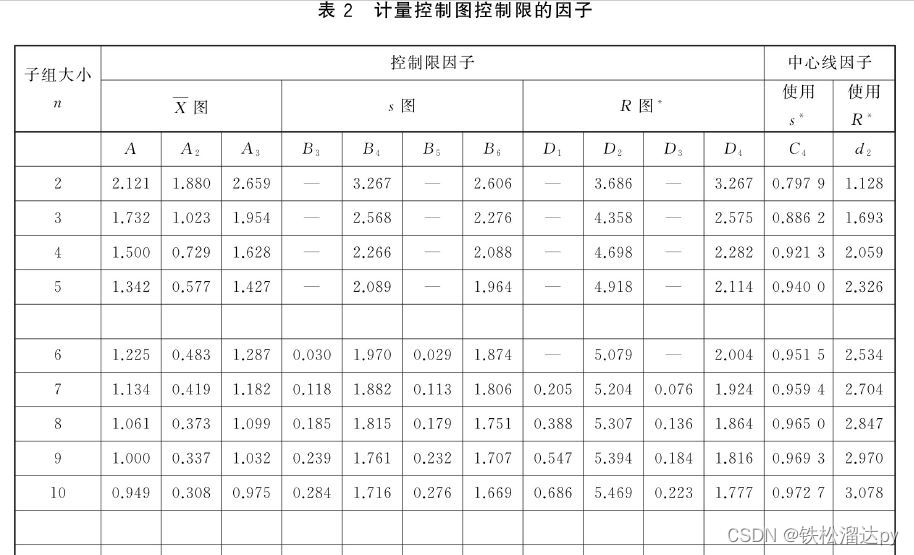
这篇关于估算总体标准差sigma = s/c4的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







