1315. 网格 - 卡特兰数

本文主要是介绍1315. 网格 - 卡特兰数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1315. 网格 - AcWing题库

 

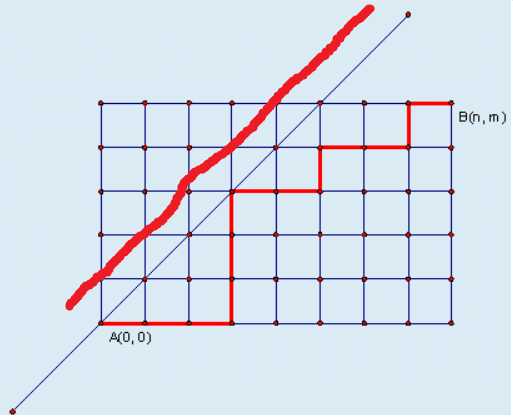
只要是触及上面这条红线的，就以第一次触及的点为起点沿红线反转，终点的位置与红线对称的位置可以看作触及红线的路线的终点。

y=x+1

横坐标容易得出时m - 1，（m + n） - (m - 1)得出纵坐标n + 1

答案就是

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef pair<int, int> PII;
typedef long long ll;
typedef long double ld;const int N = 10010;int n, m;
int primes[N], cnt;
bool st[N];void init()
{for(int i = 2; i < N; i ++){if(!st[i])primes[cnt ++] = i;for(int j = 0; primes[j] * i < N; j ++){st[primes[j] * i] = true;if(i % primes[j] == 0)break;}}
}int get(int n, int p)
{int c = 0;while(n){c += n / p;n /= p;}return c;
}vector<int> mul(vector<int> &A, int b)
{int t = 0;vector<int> C;for(int i = 0; i < A.size(); i ++){t += A[i] * b;C.push_back(t % 10);t /= 10;}while(t){C.push_back(t % 10);t /= 10;}return C;
}vector<int> C(int a, int b)
{vector<int> A;A.push_back(1);for(int i = 0; primes[i] <= a; i ++){int p = primes[i];int s = get(a, p) - get(b, p) - get(a - b, p);for(int j = 0; j < s; j ++)A = mul(A, p);}return A;
}vector<int> sub(vector<int> &A, vector<int> &B)
{vector<int> c;int t = 0;for(int i = 0; i < A.size(); i ++){t = A[i] - t;if(i < B.size())t -= B[i];c.push_back((t + 10) % 10);if(t < 0)t = 1;else t = 0;}while(c.size() > 1 && c.back() == 0)c.pop_back();return c; 
}int main()
{IOSinit();cin >> n >> m;vector<int> c1 = C(n + m, n), c2 = C(n + m, m - 1);c1 = sub(c1, c2);for(int i = c1.size() - 1; i >= 0; i --){cout << c1[i];}return 0;
} 

 

这篇关于1315. 网格 - 卡特兰数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---