本文主要是介绍哈希表的应用-浅析顶点聚簇网格简化算法的实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
本篇接顶点去重那一篇,继续使用哈希表来实现网格算法。这次介绍的是一种比较简单的网格简化算法,叫做顶点聚簇。
网格简化
为了介绍这个算法,首先说明一下网格简化算法。随着计算机绘图在现代科技领域中的广泛应用, 计算机图形在现代制造业中发挥着重要的作用。计算机图形学中对模型的要求更加精密, 也更加复杂, 生成的面片数也更加庞大, 庞大的数据量必然对计算机的计算能力提出更高要求, 对模型的生成也带来更多困难[。为此, 需要对重建得到的复杂的数学模型进行简化, 以减少数据量和数据模型的复杂程度, 这就使得网格简化的提出成为必然。模型简化也称数据缩小或数据删减, 对于实时应用来说, 通常需要这个过程来减少存储的顶点数并将这些顶点发送到图形管线。网格简化的目的是在尽量保持原模型可视特征的条件下, 减少模型的多边形数目。
网格简化方法之顶点聚簇网格削减
顶点聚簇方法又被叫做顶点聚类。顶点聚簇方法的原理首先是将原模型统一归于一个大区域,然后对大区域进行划分,使得小区域中包含了许多散落其中的顶点,再将此区域中的顶点合并,形成新的顶点,再根据原始网格的拓扑关系,把这些顶点三角化后,从而得到简化模型。下图也可以生动的说明顶点聚簇的原理。

顶点聚簇是比较简单高效的网格简化算法,不过缺点是生成结果的质量不如其他的网格简化算法。
使用顶点聚簇来简化SMC算法生成的网格
由于SMC算法生成的网格顶点坐标都是基于原来三维图像中的体素索引,所以这些顶点都可以看作是处在单位长度为1的笛卡尔网格之上。坐标范围则是从(0,0,0)到(Mesh的X最大值,Mesh的Y最大值,Mesh的Z最大值),所以实际上这样的网格可以当作已经被单位长度为1的正方体区域所划分了。这样假如想要进行顶点聚簇简化,就需要用一个大于1的浮点值为边长再来给空间划分正方体区域,这个值是用户提供的参数,下文用unitLength来指代这个参数,表示它是新的单位长度。同时不难想到unitLength越大,网格削减的越厉害。
算法可以采用在“浅议顶点焊接”一篇中的哈希表来实现,这个哈希表的作用就是为三维空间中的整点提供快速存储与查找。在顶点聚类算法中,我们可以将在一个新正方体单位区域的点都合并为一个点并存入这样的哈希表中。这样我们就能将新的点重新存在新的Mesh中,而原来的三角形用同样的道理来替换其中点的索引,最后将位退化的三角形存在新Mesh的三角形表中。
综上所述,用C#实现算法的代码如下:
public class VertexCluster {Mesh mesh;public VertexCluster(Mesh mesh){this.mesh = mesh;}public void Clear(){mesh = null;}public void ExecuteSimplification(float unitLength){if (unitLength <= 1){return;}Mesh newMesh = new Mesh();//新建Mesh存放削减后的网格Box3Float box = mesh.GetBox3();//首先获取Mesh的空间范围 XYZ方向的最大最小值存在box中int resx = (int)((box.Max3[0] - box.Min3[0]) / unitLength) + 1;int resy = (int)((box.Max3[1] - box.Min3[1]) / unitLength) + 1;int resz = (int)((box.Max3[2] - box.Min3[2]) / unitLength) + 1;//在新的单位长度下,得出新空间划分出的每一维的长度 HashTable_Double2dArray<int> hash = new HashTable_Double2dArray<int>(resx+1, resy+1, resz+1);//创建hash表,这里使用的是双二维数组哈希表for (int i = 0; i < mesh.Vertices.Count; i++){Point3d p = mesh.Vertices[i];int xindex = (int)((p.X - box.Min3[0]) / unitLength);int yindex = (int)((p.Y - box.Min3[1]) / unitLength);int zindex = (int)((p.Z - box.Min3[2]) / unitLength);//计算点在新单位长度下的坐标int value = 0;bool hasValue = hash.GetHashValue(xindex, yindex, zindex, ref value);if (!hasValue){hash.SetHashValue(xindex, yindex, zindex, newMesh.Vertices.Count);newMesh.AddVertex(new Point3d(xindex, yindex, zindex));}//新单位长度下肯定有原来不同的点映射到相同的位置,//总是添加第一次映射到这个位置的点入Mesh,之后的不再添加 }for (int i = 0; i < mesh.Faces.Count; i++){Triangle t = mesh.Faces[i];Point3d p0 = mesh.Vertices[t.P0Index];Point3d p1 = mesh.Vertices[t.P1Index];Point3d p2 = mesh.Vertices[t.P2Index];int xindex0 = (int)((p0.X - box.Min3[0]) / unitLength);int yindex0 = (int)((p0.Y - box.Min3[1]) / unitLength);int zindex0 = (int)((p0.Z - box.Min3[2]) / unitLength);int index0 = 0;hash.GetHashValue(xindex0, yindex0, zindex0, ref index0);int xindex1 = (int)((p1.X - box.Min3[0]) / unitLength);int yindex1 = (int)((p1.Y - box.Min3[1]) / unitLength);int zindex1 = (int)((p1.Z - box.Min3[2]) / unitLength);int index1 = 0;hash.GetHashValue(xindex1, yindex1, zindex1, ref index1);int xindex2 = (int)((p2.X - box.Min3[0]) / unitLength);int yindex2 = (int)((p2.Y - box.Min3[1]) / unitLength);int zindex2 = (int)((p2.Z - box.Min3[2]) / unitLength);int index2 = 0;hash.GetHashValue(xindex2, yindex2, zindex2, ref index2);if (!(index0 == index1 || index0 == index2 || index1 == index2)){newMesh.AddFace(new Triangle(index0, index1, index2));}//对于每个三角形,找出其三点对应的新位置,检查是否有两个点重合(退化),//添加不退化的三角形 }for (int i = 0; i < newMesh.Vertices.Count; i++){Point3d p = newMesh.Vertices[i];p.X = (float)(unitLength * p.X + box.Min3[0]);p.Y = (float)(unitLength * p.Y + box.Min3[1]);p.Z = (float)(unitLength * p.Z + box.Min3[2]);}//将新Mesh的坐标放大到和原来一样的尺度 mesh.Clear();mesh.Vertices = newMesh.Vertices;mesh.Faces = newMesh.Faces;//替换旧Mesh的数据 } }
算法测试
数据采用Engine数据,下表展示了算法的结果。
| - | 简花前 | 简化后 | |
| 数据预览 |  | 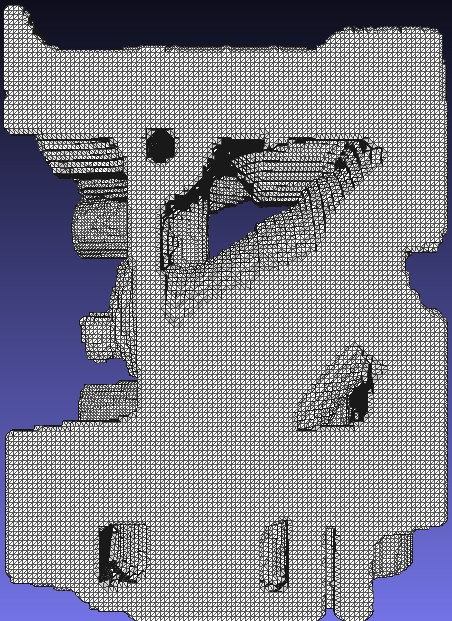 | |
| 顶点数 | 216147 | 110910 | |
| 三角形数 | 432370 | 220528 | |
| 单位长度 | 1.0 | 1.5 | |
| 削减比例(顶点) | - | 48.7% | |
| 削减比例(三角形) | - | 49.0% |
可以看出,顶点聚簇算法均匀的减少了三角网格的密度。
这篇关于哈希表的应用-浅析顶点聚簇网格简化算法的实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





