本文主要是介绍详解DFS(深度优先搜索)算法+模板+指数+排列+组合型枚举+带分数四道例题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
前言:
1.背景
2.图解分析
3.算法思想
4.dfs四大例题
4.1.递归实现指数型枚举
题解:
4.2.递归实现排列型枚举
题解:
字典序:
4.3.递归实现组合型枚举
题解:
4.4.带分数
题解:
5.最后:
前言:
大家好呀,我是山上雪,时隔多日终于回归,归功于小姑娘的打赏激励以及佬们日更一篇的节奏使得我坐不住了!!
激动万分的写下了该篇博客,文有不足,望各位大佬批评指正
动力源泉如下!!!!!!!!!
1.背景
深度优先算法(Depth First Search,简称DFS):本文均采用递归方式,搜索每一条路径,一路走到黑直到不能再走则返回,每个结点仅访问一次。
2.图解分析
对于这个图
我们想到 7这个地方的话怎么走呢?1是起点,有5条可能的路径
1-2-5
1-2-6
1-3-7(成功)
1-3-8
1-4
可以看出,想要到7则需要遍历所有可能路径,如果加一条件,找到则退出是可以减少计算量的
3.算法思想
dfs中最重要的算法思想是回溯和剪枝。
回溯就是当你面对多条路的时候,你优先选择一条路后,当你选择多条路的另一条路的时候你需要回到初始状态,也就是说,这条路走不通你就退回,然后选择下一条路,满足回溯条件的某个状态的点称为“回溯点”。
剪枝,因为dfs算法用的递归实现,这时候就可能产生了许多不必要的计算过程,而这些计算过程通常很大。所以我们就可以加一个限制条件,使其不用计算直接返回,这种思想就像是剪掉了树的枝条,所以称为“剪枝”。
4.dfs四大例题
4.1.递归实现指数型枚举
从 1∼n这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 n。
输出格式
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 1个空格隔开。
对于没有选任何数的方案,输出空行。
本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围
1≤ n ≤15
输入样例:
3输出样例:
3 2 2 3 1 1 3 1 2 1 2 3
题解:
这个题关键是按什么顺序枚举,可以对每个数进行分类 选或者不选以及上一个状态 然后输出所有可能性即可
这里考虑开一个数组用来记录每个数的状态
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=16;//一半空间开大一点,使其从下标1开始容易判断,避免越界
int sd[N];//这里全区变量的话默认数组值为1 状态数组 0为没选 1为选择 2为不选
int cin=0;
//int arr[][N];可以直接输出数,也可以先存在二维数组里再输出
int n;
void dfs(int u)//这里的u代表正在选择的第几个数
{if(u>n)//u大于n则代表已经分析好了n个数,则可以退出{for(int i=1;i<=n;i++){if(sd[i]==1)printf("%d ",i);//枚举1到n的每个数,根据状态选择是否打印}puts("");//相当于printf("\n");return ;}sd[u]=1;//表示当前第u个数可以选择dfs(u+1);//继续判断下一个数sd[u]=0;//恢复现场,本来是1则还是1sd[u]=2;//表示该条路不选第u个数dfs(u+1);//继续判断在该种情况下的下一个数sd[u]=0;//恢复现场}
int main()
{cin >> n;dfs(1);//因为先判断第一个数则初始值为1
return 0;
}4.2.递归实现排列型枚举
把 1∼n 这 n 个整数排成一行后随机打乱顺序,输出所有可能的次序。
输入格式
一个整数 n。
输出格式
按照从小到大的顺序输出所有方案,每行 1个。
首先,同一行相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面。
数据范围
1≤ n ≤9
输入样例:
3输出样例:
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
题解:
字典序:
比如两个数列:A:a1 a2 a3....an和B:b1 b2 b3.....bn
根据序号比较假如想要A>B的话从a1和b1开始比较相等则比较下一个,直到am>bm则算A>B
同理B>A情况相反
而这里只要保证拍的时候数列是升序的,则依次输出的结果就会按照字典序排列
有两种思想:1.依次枚举每个数放到哪个位置
2.依次枚举每个位置放哪个数
下边用的是思想2
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=10;
int stede[N];//全局定义时默数据认为0 保存某个位置时对应的某个数
bool used[N];//全局定义时默认是false 记录该数是否被选过,选过则不再选
int n;
void dfs(int u)//u表示正在排第u个位置
{if(u>n)//表示已经排满n个位置,可以输出了{for(int i=1;i<=n;i++){printf("%d ",stede[i]);//输出数据}puts("");//换行return ;}for(int i=1;i<=n;i++)//从小到大枚举没放过的数{if(!used[i])//状态为没放过的可以进入{stede[u]=i;//第u个位置放iused[i]=true;//数i则改变状态为放过dfs(u+1);//继续判断下一个位置stede[u]=0;//恢复现场used[i]=false;//在上一步中该数没被选过,恢复现场}}}
int main()
{cin>>n;dfs(1);return 0;
}4.3.递归实现组合型枚举
从 1∼n 这 n个整数中随机选出 m个,输出所有可能的选择方案。
输入格式
两个整数 n,m在同一行用空格隔开。
输出格式
按照从小到大的顺序输出所有方案,每行 1个。
首先,同一行内的数升序排列,相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面(例如
1 3 5 7排在1 3 6 8前面)。数据范围
n>0 ,
0≤m≤n
n+(n−m)≤25输入样例:
5 3输出样例:
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
题解:
三个位置可以放哪些数,放满则返回数值,这道题跟上边大同小异,可以看到要选出m个数,所以该题有些情况可以不用考虑直接返回的,用到了剪枝思想
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int n,m;
const int N=20;int st[N];//存放某个位置上放某个数
void dfs(int u,int start)//u代表第u个位置 start因为同一行内要求升序,所以下一个位置要从比该位置大的数开始枚举
{if(u+n-start<m)//当满足该条件时选不够m个数,则直接返回return ;if(u==m+1)//此时u个位置均填满是,输出即可{for(int i=1;i<=m;i++){printf("%d ",st[i]);}puts("");return ;}for(int i=start;i<=n;i++){st[u]=i;//第u个位置填idfs(u+1,i+1);st[u]=0;//恢复现场}
}
int main()
{cin>>n>>m;dfs(1,1);return 0;
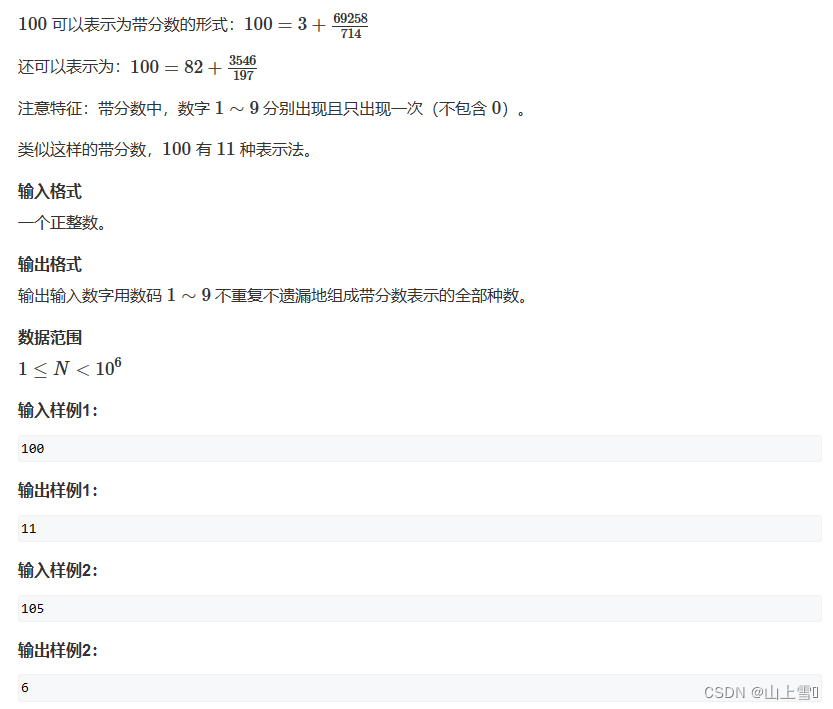
}4.4.带分数
题解:
等式可看成N=a+b/c;
该题直接看感觉不好看,但是我们读题啊,1~n的数都出现,然后分成三段a b c这不就相当于是全排列,然后分三个区间分别将数组里的数转为一个整数,最后再参与运算,满足则计数器加1即可
即满足:c*N=a*c+b;
所以该题
1.通过dfs函数得到全排列的所有组合
2.将每个组合分成三段,枚举出所有分成三段的情况
3.将每段转化成整数,判断该整数是否满足等式
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=20;
int n;
int cn=0;//计数器,满足等式则+1
bool sf[N];//记录数是否被选过
int sd[N];
int call(int i,int j)//将每段转化成整数输出,i和j把全排列分成三段
{int num=0;for(;i<=j;i++)
num=num*10+sd[i];return num;
}
void dfsabc()//接收dfs函数传来的每个序列,并进行判断
{
int a,b,c;
for(int i=1;i<=6;i++)//因为N最大是1000000,所以最大是7位数,可以减少计算
{for(int j=i+1;j<=8;j++){a=call(1,i);b=call(i+1,j);c=call(j+1,9);if(c*n==a*c+b)cn++;}
}
}
void dfs(int u)
{if(u>9){dfsabc();//将排列好的序列传给dfsabc加工判断return ;}for(int i=1;i<=9;i++){if(!sf[i]){sd[u]=i;sf[i]=true;dfs(u+1);sd[u]=0;sf[i]=false;}}
}
int main()
{cin>>n;dfs(1);printf("%d",cn);return 0;
}5.最后:
dfs深度搜索算法属于算法的入门级别,建议配合着画图学习效果更佳
码文不易,求三连~
这篇关于详解DFS(深度优先搜索)算法+模板+指数+排列+组合型枚举+带分数四道例题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!