本文主要是介绍R实现动态条件相关模型与GARCH模型结合研究中美股市动态相关性(DCC-GARCH模型),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
大家好,我是带我去滑雪!
中美两国是全球最大的经济体,其经济活动对全球产业链和贸易体系都具有巨大影响。中美之间的经济互动包括大规模的贸易、投资和金融往来。这些互动不仅仅反映在经济数据上,还体现在股市上。中美股市的联动关系反映了全球化时代的现实。它们的表现不仅关乎两国自身经济,还对全球经济和金融市场有着深远的影响。因此,了解和关注这种联动关系对投资者、政策制定者和全球市场观察者来说都至关重要。本期使用DCC-GARCH模型研究近20年中美股市的动态相关性。
目录
一、数据搜集与预处理
(1)收益率的描述统计
(2)ADF平稳性检验
(3)ARCH效应检验
(4)绘制指数与收益率的时序图
二、DCC-GARCH的估计
(1)估计结果
(2) 绘制DCC估计后的条件均值图、条件方差图、条件协方差图 、动态条件相关系数图
一、数据搜集与预处理
目标是选用S&P综合指数(GSPC)的周对数收益率作为美国股市的市场收益率,选用上证综合指数(SSEC)的周对数收益率作为中国股市的市场收益率。数据样本区间为1997年7月到2017年7月,共计1048例收盘价,数据均来源于雅虎财经。由于获取的原始数据是指数的收盘价,因此可以先求得指数的收益率,并放大100倍。下面对收益率进行时间序列数据建模前的各自准备工作,包括收益率的描述统计、平稳性检验、ARCH效应检验,下面分别一一进行。
install.packages("fBasics",repos="http://mirrors.tuna.tsinghua.edu.cn/CRAN/")
install.packages("FinTS",repos="http://mirrors.tuna.tsinghua.edu.cn/CRAN/")
install.packages("rmgarch",repos="http://mirrors.tuna.tsinghua.edu.cn/CRAN/")
install.packages("MTS",repos="http://mirrors.tuna.tsinghua.edu.cn/CRAN/")
library(fBasics);library(FinTS);library(tseries)
library(rmgarch);library(MTS)#安装并调用包
dat1.tmp <- read.csv("E:/GSPC.csv"); head(dat1.tmp)
dat2.tmp <- read.csv("E:/SSEC.csv"); head(dat2.tmp)#导入数据
dat1=xts::as.xts(dat1.tmp[,2],as.Date(dat1.tmp[,1]))
dat2=xts::as.xts(dat2.tmp[,2],as.Date(dat2.tmp[,1]))
head(dat1);head(dat2)#将导入的数据转换为时间序列格式
R1=diff(log(dat1))*100;R1=R1[-1] #Compute Returns
names(R1)="GSPC";head(R1)R2=diff(log(dat2))*100;R2=R2[-1] #Compute Returns
names(R2)="SSEC" ;head(R2)#求得指数的收益率,并放大100倍
输出结果:
SSEC
1997-07-13 4.658029
1997-07-20 -3.276194
1997-07-27 1.858668
1997-08-03 1.102607
1997-08-10 -5.364068
1997-08-17 2.485685GSPC
1997-07-13 -0.1506572
1997-07-20 2.5339921
1997-07-27 0.8855145
1997-08-03 -1.4463145
1997-08-10 -3.5689432
1997-08-17 2.4919732
(1)收益率的描述统计
DataRet=na.omit(cbind(R1,R2));#去除缺失值
tail(DataRet);nrow(DataRet)#展示最后6行,并计算收益率长度输出结果:
GSPC SSEC
2017-06-25 -0.61254923 1.0882729
2017-07-02 0.07301175 0.7965253
2017-07-09 1.39588457 0.1385001
2017-07-16 0.53814120 0.4818579
2017-07-23 -0.01779466 0.4701144
2017-07-30 0.19115167 0.2713932
[1] 1047
basicStats(DataRet)输出结果:
GSPC SSEC
nobs 1047.000000 1047.000000
NAs 0.000000 0.000000
Minimum -20.083751 -14.897934
Maximum 11.355896 13.944743
1. Quartile -1.137209 -1.738476
3. Quartile 1.404862 1.904221
Mean 0.094936 0.099183
Median 0.196563 0.050927
Sum 99.397639 103.844343
SE Mean 0.076118 0.103059
LCL Mean -0.054426 -0.103043
UCL Mean 0.244297 0.301408
Variance 6.066269 11.120290
Stdev 2.462980 3.334710
Skewness -0.775533 -0.128495
Kurtosis 6.394769 2.291610
(2)ADF平稳性检验
adf.test(R1);
输出结果:
Augmented Dickey-Fuller Test
data: R1
Dickey-Fuller = -9.8464, Lag order = 10, p-value = 0.01
alternative hypothesis: stationaryadf.test(R2);
输出结果:
Augmented Dickey-Fuller Test
data: R2
Dickey-Fuller = -8.1659, Lag order = 10, p-value = 0.01
alternative hypothesis: stationary
由于 时间序列数据进行建模时,需要了解数据的平稳性,以保证模型的有效性。通过ADF检验可以发现中美股市收益率是平稳的。
(3)ARCH效应检验
ArchTest(R1,lags=15,demean=T)
输出结果:
ARCH LM-test; Null hypothesis: no ARCH effects
data: R1
Chi-squared = 158.22, df = 15, p-value < 2.2e-16ArchTest(R2,lags=15,demean=T)
输出结果:
ARCH LM-test; Null hypothesis: no ARCH effects
data: R2
Chi-squared = 127.52, df = 15, p-value < 2.2e-16
通过ARCH检验可以发现中美股市收益率之间存在ARCH效应,说明可以运用GARCH模型。
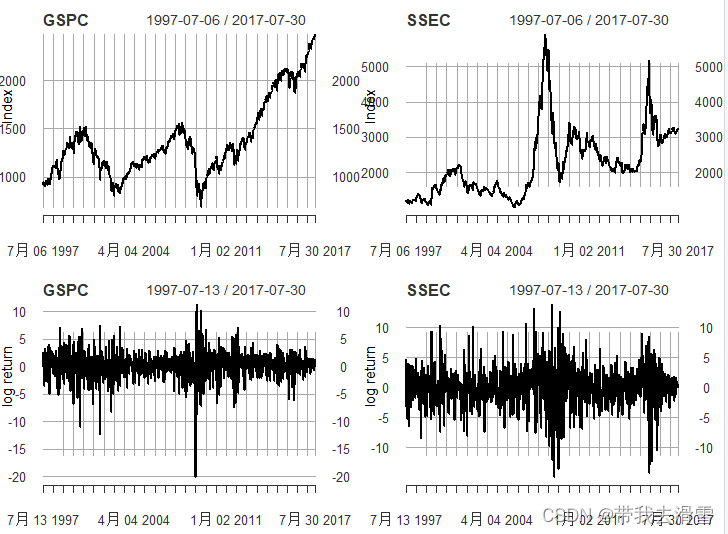
(4)绘制指数与收益率的时序图
opar=par(no.readonly=T)
par(mfrow=c(2,2))
plot(dat1,main="GSPC",xlab="Time",ylab="Index")
plot(dat2,main="SSEC",xlab="Time",ylab="Index")
plot(R1,main="GSPC",xlab="Time",ylab="log return")
plot(R2,main="SSEC",xlab="Time",ylab="log return")
par(opar)输出结果:
通过时序图可以发现,美国收益率指数虽然在互联网泡沫和次贷危机期间大幅度下降,但大部分时期指数是上涨的。而中国指数在2007年到2008年以及2015年到2016年两个时间段显著大涨大跌,其他时期的走势相对平稳,但上行行情远没有美国的多。通过收益率的时序图可以发现,中美两国收益率都存在显著的波动聚集现象,并且中国的波动幅度大于美国的波动。
二、DCC-GARCH的估计
(1)估计结果
n=ncol(DataRet)
p=1;q=1
meanSpec=list(armaOrder=c(1,0),include.mean=TRUE,archpow=1)
varSpec=list(model="sGARCH",garchOrder = c(p,q))
distSpec=c("mvt") #c("mvnorm", "mvt", "mvlaplace")spec1=ugarchspec(mean.model=meanSpec,variance.model=varSpec)
mySpec=multispec(replicate(n, spec1))mySpec=dccspec(mySpec, VAR=F, robust=F, lag=1, lag.max=NULL,lag.criterion=c("AIC"), external.regressors = NULL, robust.control = list(gamma = 0.25, delta = 0.01, nc = 10, ns = 500), dccOrder = c(1, 1), distribution = distSpec, start.pars = list(), fixed.pars = list())
fit_dcc=dccfit(data=DataRet, mySpec, out.sample=10, solver="solnp", solver.control = list(), fit.control = list(eval.se = TRUE, stationarity = TRUE, scale = FALSE), parallel = TRUE, parallel.control = list(pkg = c("multicore"), cores = 2), fit = NULL, VAR.fit = NULL)
RSD=residuals(fit_dcc);
show(fit_dcc)输出结果:
*---------------------------------*
* DCC GARCH Fit *
*---------------------------------*Distribution : mvt
Model : DCC(1,1)
No. Parameters : 14
[VAR GARCH DCC UncQ] : [0+10+3+1]
No. Series : 2
No. Obs. : 1037
Log-Likelihood : -4863.167
Av.Log-Likelihood : -4.69Optimal Parameters
-----------------------------------
Estimate Std. Error t value Pr(>|t|)
[GSPC].mu 0.215241 0.055014 3.9125 0.000091
[GSPC].ar1 -0.112713 0.034833 -3.2359 0.001213
[GSPC].omega 0.302235 0.131215 2.3034 0.021259
[GSPC].alpha1 0.196408 0.060734 3.2339 0.001221
[GSPC].beta1 0.762232 0.064558 11.8069 0.000000
[SSEC].mu 0.078023 0.096492 0.8086 0.418748
[SSEC].ar1 0.053512 0.034308 1.5598 0.118816
[SSEC].omega 0.388848 0.206514 1.8829 0.059712
[SSEC].alpha1 0.117551 0.036551 3.2161 0.001300
[SSEC].beta1 0.848819 0.047688 17.7993 0.000000
[Joint]dcca1 0.013581 0.007305 1.8591 0.063013
[Joint]dccb1 0.971799 0.011366 85.5008 0.000000
[Joint]mshape 8.290728 1.110120 7.4683 0.000000Information Criteria
---------------------
Akaike 9.4063
Bayes 9.4730
Shibata 9.4059
Hannan-Quinn 9.4316
Elapsed time : 3.121074
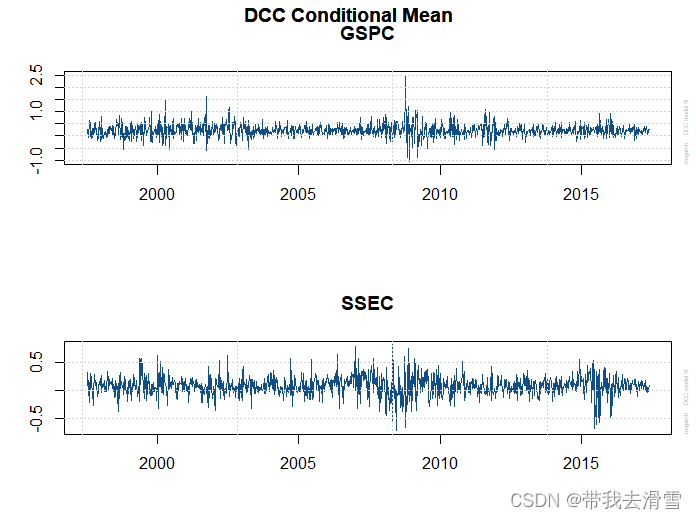
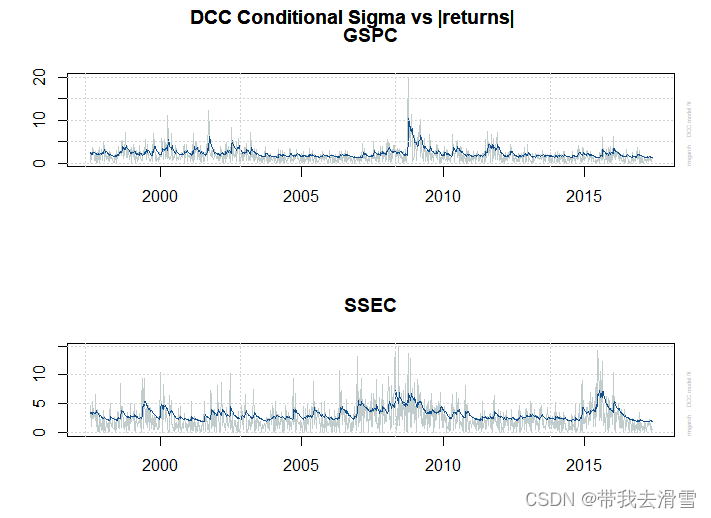
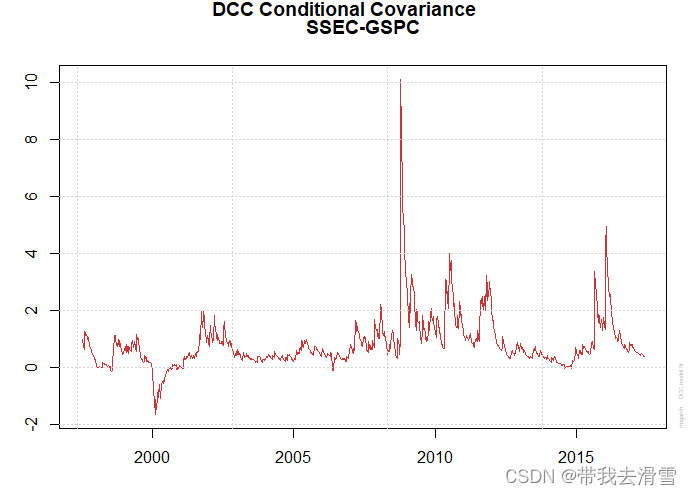
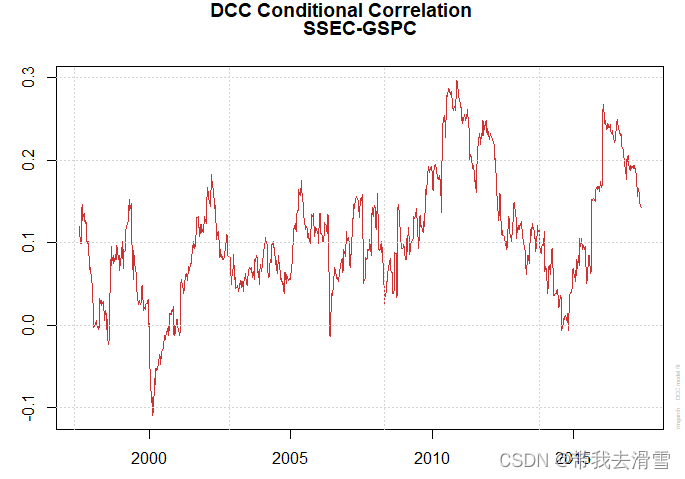
(2) 绘制DCC估计后的条件均值图、条件方差图、条件协方差图 、动态条件相关系数图
plot(fit_dcc)
需要数据集的家人们可以去百度网盘(永久有效)获取:
链接:https://pan.baidu.com/s/1E59qYZuGhwlrx6gn4JJZTg?pwd=2138
提取码:2138
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!
这篇关于R实现动态条件相关模型与GARCH模型结合研究中美股市动态相关性(DCC-GARCH模型)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!