本文主要是介绍图解辗转相除法(欧几里得算法)求解最大公约/最小公倍数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
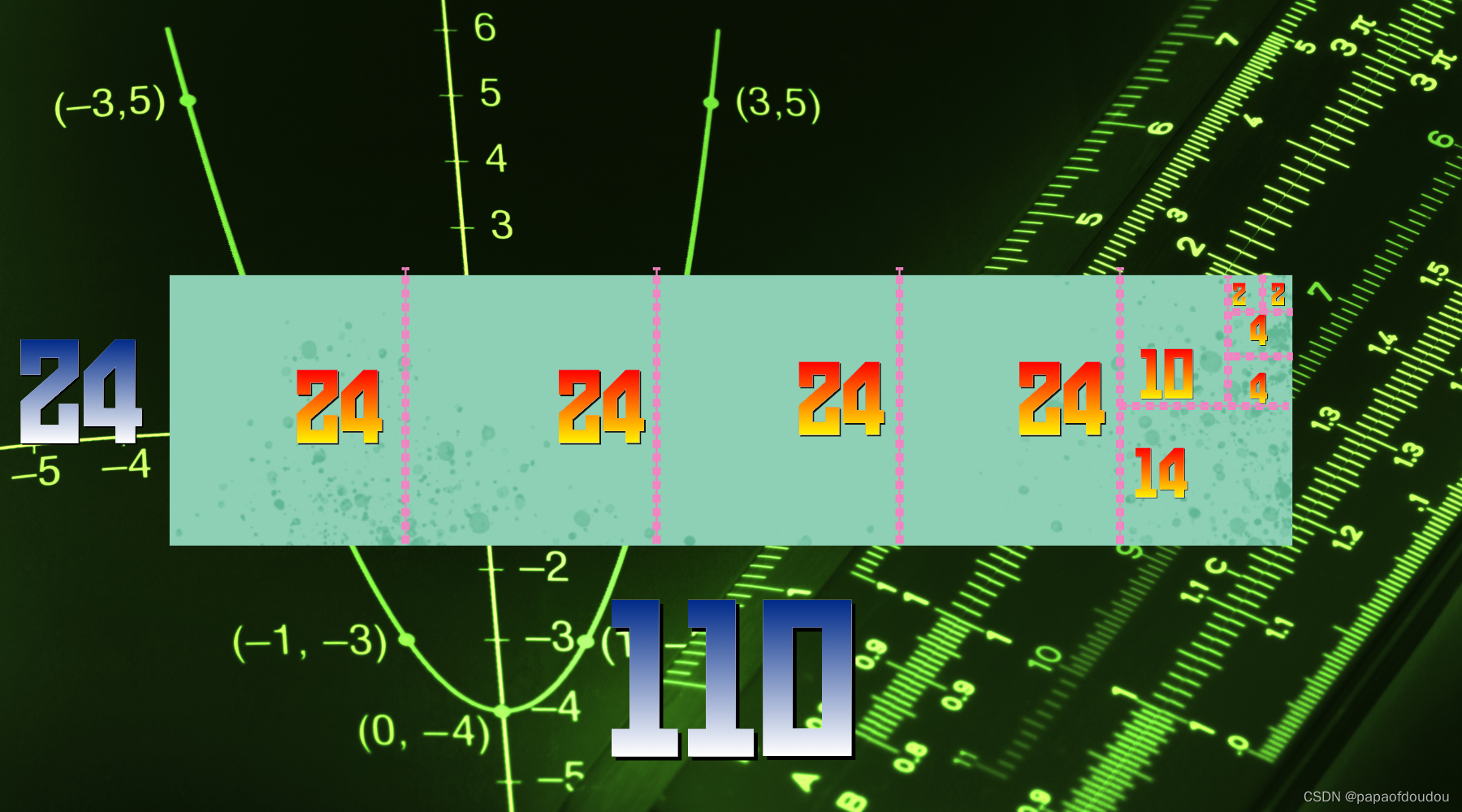
公元前300的欧几里德,已经会用如下的辗转相除计算110和24的最大公约数了:
程序实现
gcd(a, b)= gcd(b, a % b)= gcd(a%b, b %(a%b)) ....
先上辗转相除法(欧几里得算法)的三种代码实现:
#include <stdio.h>
#include <stdlib.h>int gcd1(int a, int b)
{int ret;while(1){if(a >= b){a = a%b;if(a == 0){ret = b;break;}}else{b = b %a;if(b == 0){ret = a;break;}}}return ret;
}int gcd2(int a,int b)
{if(b == 0)return a;return gcd2(b,a%b);
}int gcd3(int a,int b)
{while(b){int t = b;b = a%b;a = t;}return a;
} int main(void)
{int a, b;a= 100;b = 45;printf("%s line %d, res1 %d, res2 %d, res3 %d.\n", __func__, __LINE__, gcd1(a, b), gcd2(a, b), gcd3(a, b));return 0;
}
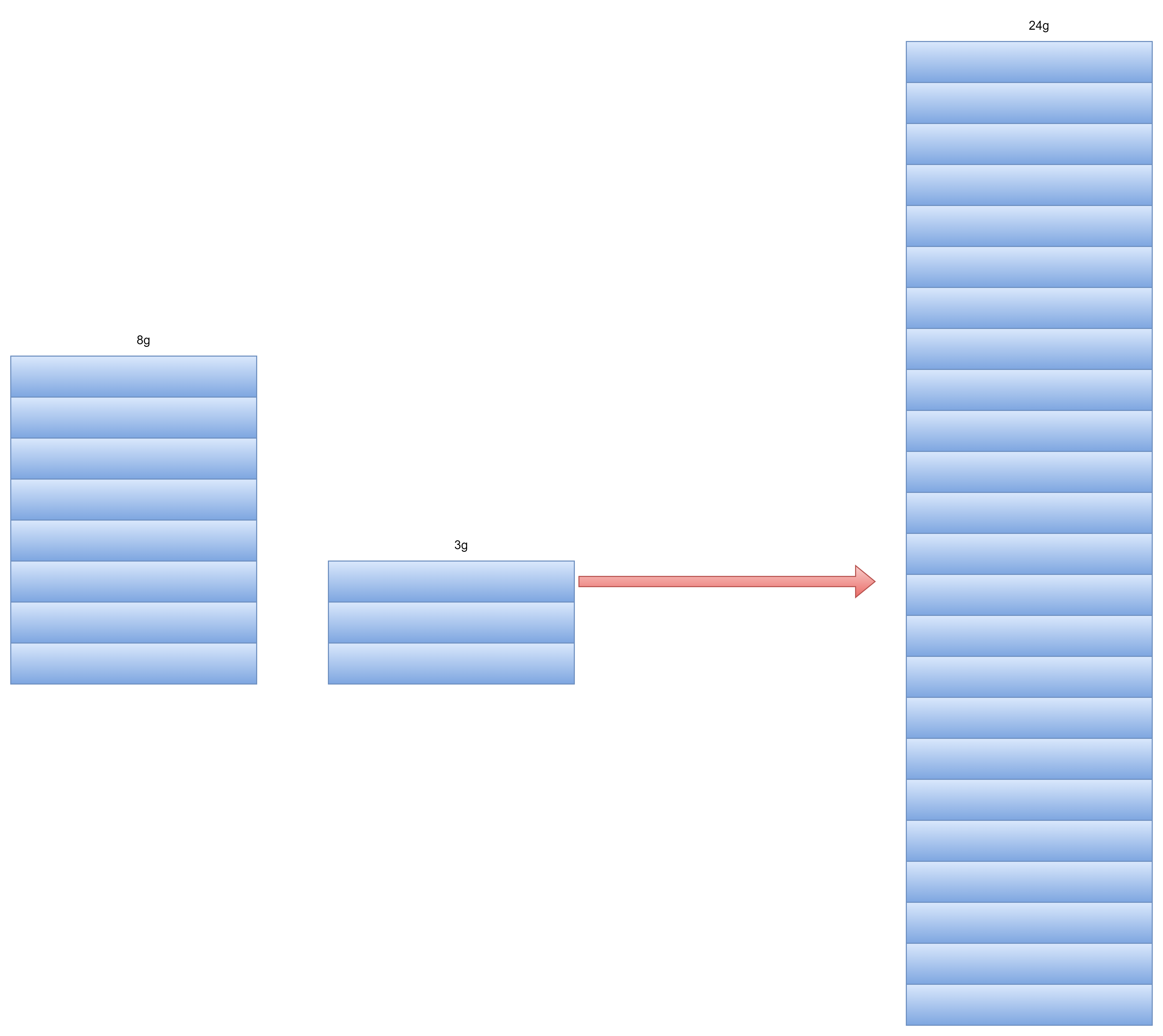
下面用一幅图示解题过程,图中蓝色的矩形单元表示一个最小公约的单元。它具有以下性质:
1.以最小公约表示的两个原数字互质。(这是必然,反证法,如果不互质,则可以提取一个共同的因子重新定义最小公约单元,直到表示为互质,比如图中的8和3互质)。
2.辗转相除的每个阶段的两个数字也均互质,证明过程类似,反正法即可(当前辗转阶段如果存在共同的约数,则必然传递到之前的阶段也都有同样的约数,所以同理最小公约单元也要重新定义,直到每级辗转互质)。
基于以上两个严密的逻辑,辗转相除一定能够找到组成两个数字的最基本的公约块儿,它是两个数字共有的零件。

扩展-求最小公倍数
既然上一步已经计算得到了最小公约数,并且得到了以最小公约表示的两个原数字互质的推论,就不难得到计算最小公倍数的公用公式。
通用算法,已知数字m,n的最大公约数是g,则m/g, n/g互质,两个互质的数的最小公倍数就是两个质数之积,所以,最小公倍数为
由于单元为g,所以最小公倍数的真实值为:
#include <stdio.h>
#include <stdlib.h>int gcd1(int a, int b)
{int ret;while(1){if(a >= b){a = a%b;if(a == 0){ret = b;break;}}else{b = b %a;if(b == 0){ret = a;break;}}}return ret;
}int gcd2(int a,int b)
{if(b == 0)return a;return gcd2(b,a%b);
}int gcd3(int a,int b)
{while(b){int t = b;b = a%b;a = t;}return a;
} int lcm1(int a, int b)
{int g_c_d = gcd1(a, b);return a*b/g_c_d;
}int lcm2(int m, int n)
{int mn, r ;if(m<n){mn = m ; m = n ; n = mn;}mn = m * n ;//俩个数的乘积r = m % n ;while(r!=0){m = n ;n = r ;r = m % n ;}return mn/n; //n为最大公约数
}int main(void)
{int a, b;a= 100;b = 45;printf("%s line %d, res1 %d, res2 %d, res3 %d, lcm1 %d, lcm2 %d.\n", __func__, __LINE__, gcd1(a, b), gcd2(a, b), gcd3(a, b), lcm1(a, b), lcm2(a,b));return 0;
}main line 84, res1 5, res2 5, res3 5, lcm1 900, lcm2 900.图解:
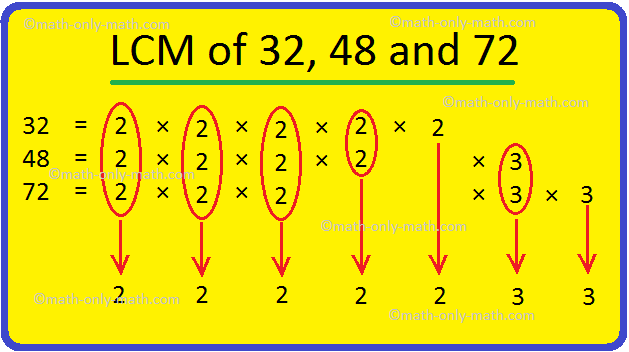
LCM of 32, 48 and 72 = 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288
关于两个互质数的最小公倍数是两数之积,可以证明如下,假设a,b两数互质,也就是两数没有1以外的公约数,则最小公倍数是axb.
不失一般情况,假设a<b,则a的倍数从小到大排列为a,2a,3a,......(b-1)a, ba;在ba之前的所有a的倍数中,假设ka(1<k<b)同样也是b的倍数,则
是整数。
由于a,b互质,则a/b不可能存在导致结果为整数的因子,所以只有k存在这个因子,但是k小于b,所以同样得到结论,这样的K不存在,这样,最小的公倍数只能是ab了,结论得证。
或者用反证法,我们知道ab一定是公倍数,要证明是最小,其它公倍数对最小公倍数之间一定可以整除(其他公倍数之间不一定),所以假设ab/n是其最小公倍数,则根据ab/n整除a,b可以推理出n是a,b的公因数,这和a,b互质矛盾。
上面那句虽然结论正确,但是推理显然是错误,反例如下40*5/25 = 8. 但是40和5任何一个都不能整除25,所以得不到ab/n整除,n是a,b公因数的结论.倒是可以证明:
ab/n为整数,则a,b一定不互质,因为假如a,b互质,则设m=ab,ab为m的一个质因数分解.根据算数基本定理,这个指因数分解唯一.如果存在c=ab/n=m/n,则必然存在m=cn,n小于a,b的情况下则m又引入了一个非a,b的因子n和c,不管n,c是质数还是合数,都违背了算数基本定理的唯一性要求.所以得证.
PS:
只有当a,c互质,且ab/c整除时,才能得出b/c整除的结论,40*5/25由于无论40或者5都和25不互素,所以,不适用于这个结论,无论40或者5都无法整除25.
关于这个定义,初等数论中的描述如下:
如果a,b和c是正整数,满足(a,b)=1.且a|bc,则a|c.
证明如下:
由于(a,b)=1,也就是a,b互素,存在整数x,y,使得ax+by=1,等式两边同时乘以c,得到acx+bcy=c.
由于bc能够整除a,所以a*cx+bc*y实际上是两个能够整除a的整数的线性组合(cx,y为系数),所以a*cx+bc*y也能够整除a. 而a*cx+bc*y等于什么呢?它就等于c,所以a|c. 结论得到证明。
或者通过欧几里德定理证明,素数的唯一分解角度:
(a,b)=1.且a|bc,如果将a,b,c三个数字进行欧几里德素数分解,则a,b互素,所以它们一定没有除1以外的共因子。 因此c必须包含所有a的素因子,并且唯一,因此a一定能够整除c.
总结:
基本原理:两个整数的最大公约数等于,其中较小的数和两数的差的最大公约数。
个人解析:若A、B有最大公约数K(A > B),则,A、B、(A - B)、A mod B(A / B的余数),都是K的倍数。即余数(A - B)和 B 的最大公公约数也是 K 。
由此递归,可知当 A mod B = 0,即 A 是 B 的倍数时,此时,B 即为 K 。实际上,存在如下定理:
两数最大公约数与最小公倍数的积等于两数之积,用公式表示就是:
当
时
最大公因数*最小公倍数=pq。
这个证明过程也很简单,假设a,b互质,那么它们的最小公倍数是ab,最大公因数1,满足题设。
加入a,b不互质,则必然存在质数p,q,使的a = sp,b=sq, s为整数。则最小公倍数为spq,最大公约数为s.同样满足题设。
图形化表示辗转相除获取最大公约数
证明: gcd(a,b) = gcd(b, a%b).
设c=gcd(a,b). 则:
a = mc
b = nc
并且m,n互素(假如m,n有公因子,则一定可以抽取出来和c作乘积产生新的最大公约数,而前提我们已经设定c为最大公约了,所以一定有办法让m,n互素).
a=qb+r=>mc=qnc+r =>r=mc-qnc = (m-qn)c.
所以c仍然是a%b的因子。
又因为m-qn和n互素(证明如下,假如m-qn和n有非1公因子s,gcd(n, m-qn) = s, n=xs, m-qn=ys.
则,r=(m-qn)c = ysc, a=qxsc+ysc, b = xsc.所以a,b的公因子是少是sc而非c. 或者这样理解:
m-qn=x*s, n=y*s=>m=(qy+x)s,所以,m,n有公因子s,和m,n互素矛盾,所以m-qn和n互素)。
所以,b=nc和a%b=(m-qn)c的最大公因子也是c(否则n和m-qn一定能抽取另一个公因子和C相乘得到新的最大公因子,矛盾)。
所以, gcd(a,b) = gcd(b, a%b).b, a%b和a,b有相同的最大公因子。
从下图也可以看出,如果某级运算出现了新的更大的公约数,则这个公约数一定会反推回a,b,导致更新前提,所以GCD的运算会保持最大公约数不变。
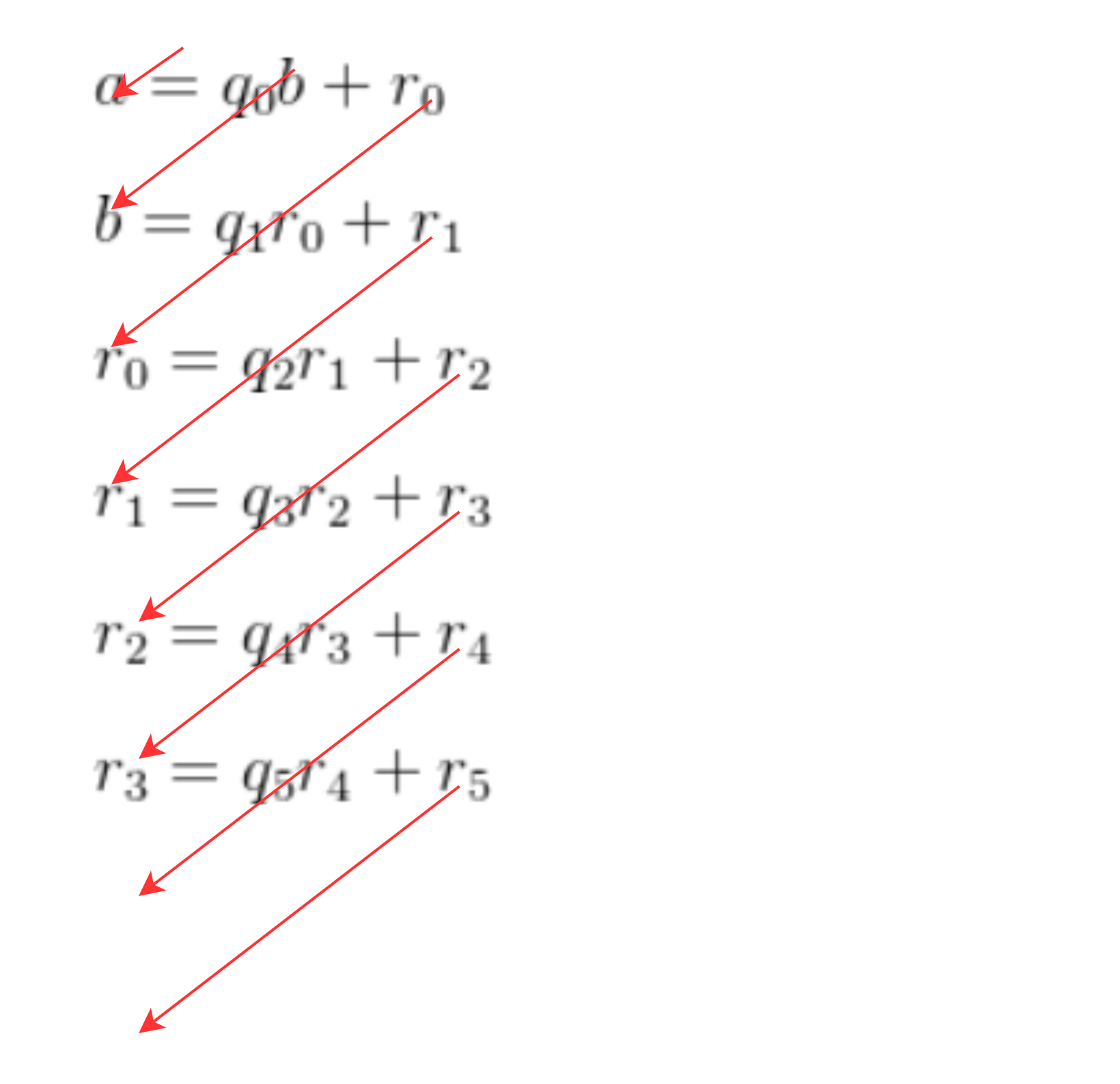
下图展示了欧几里得算法的一个几何解释,反复剪掉正方形,用最终的小正方形铺满整个原图。
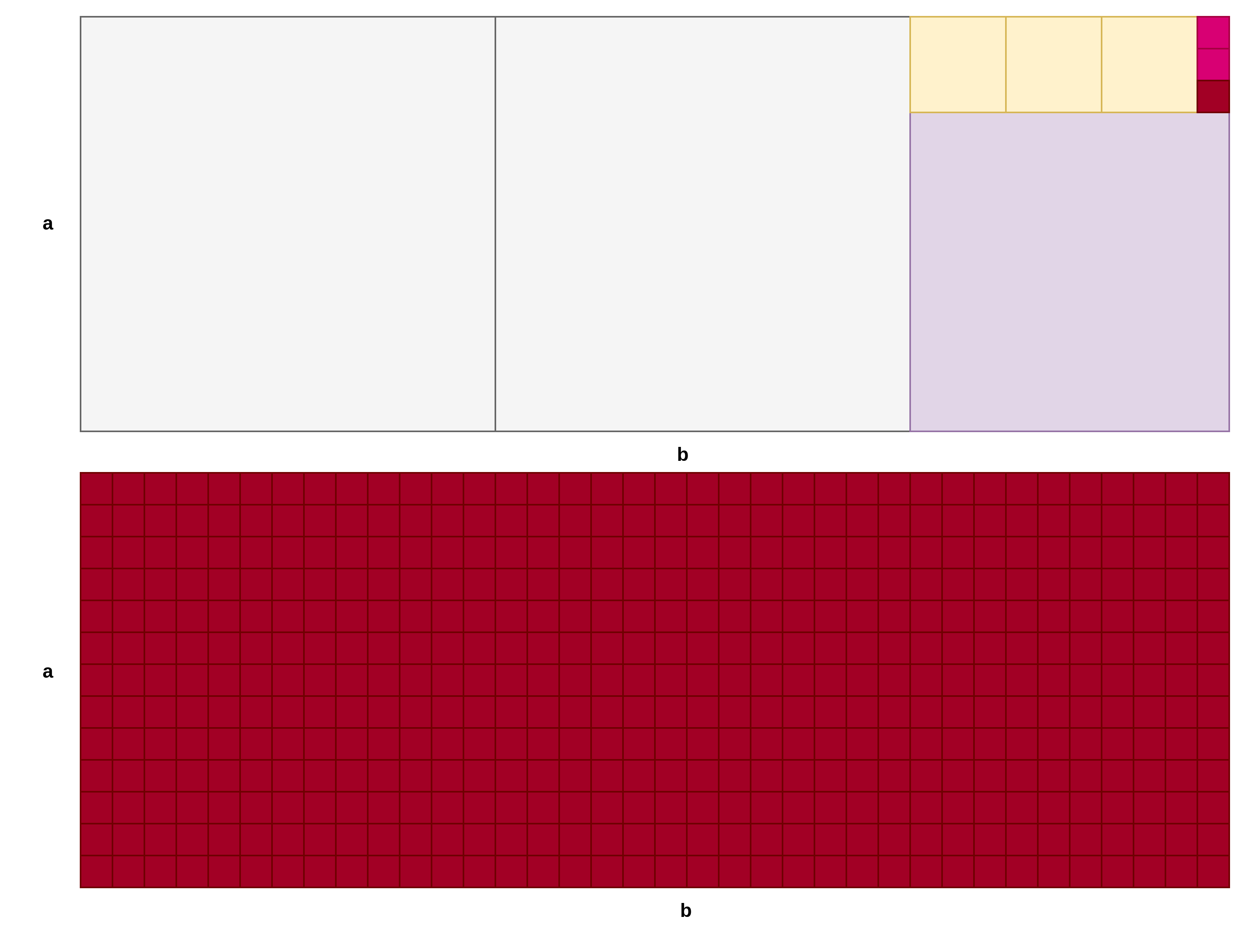
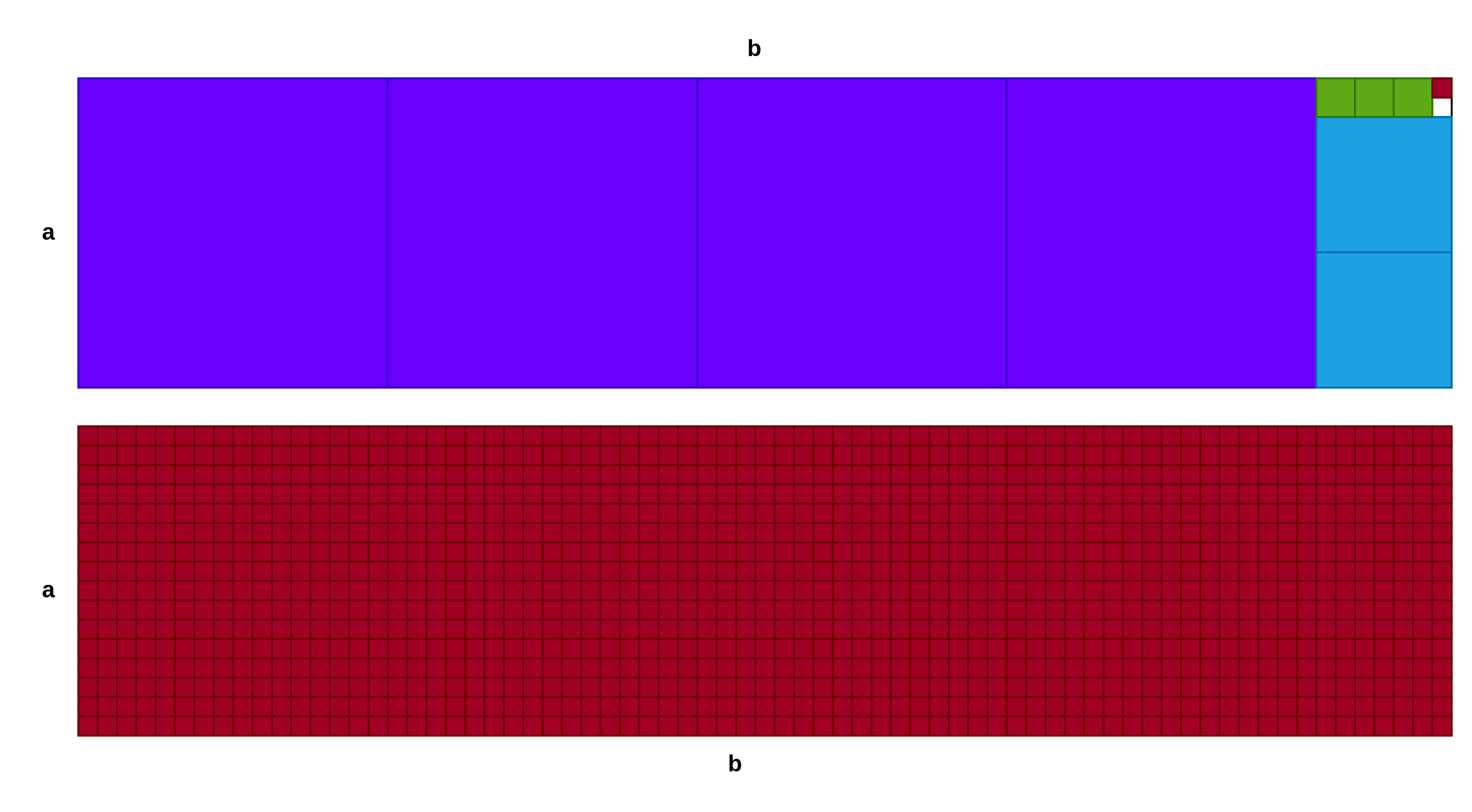
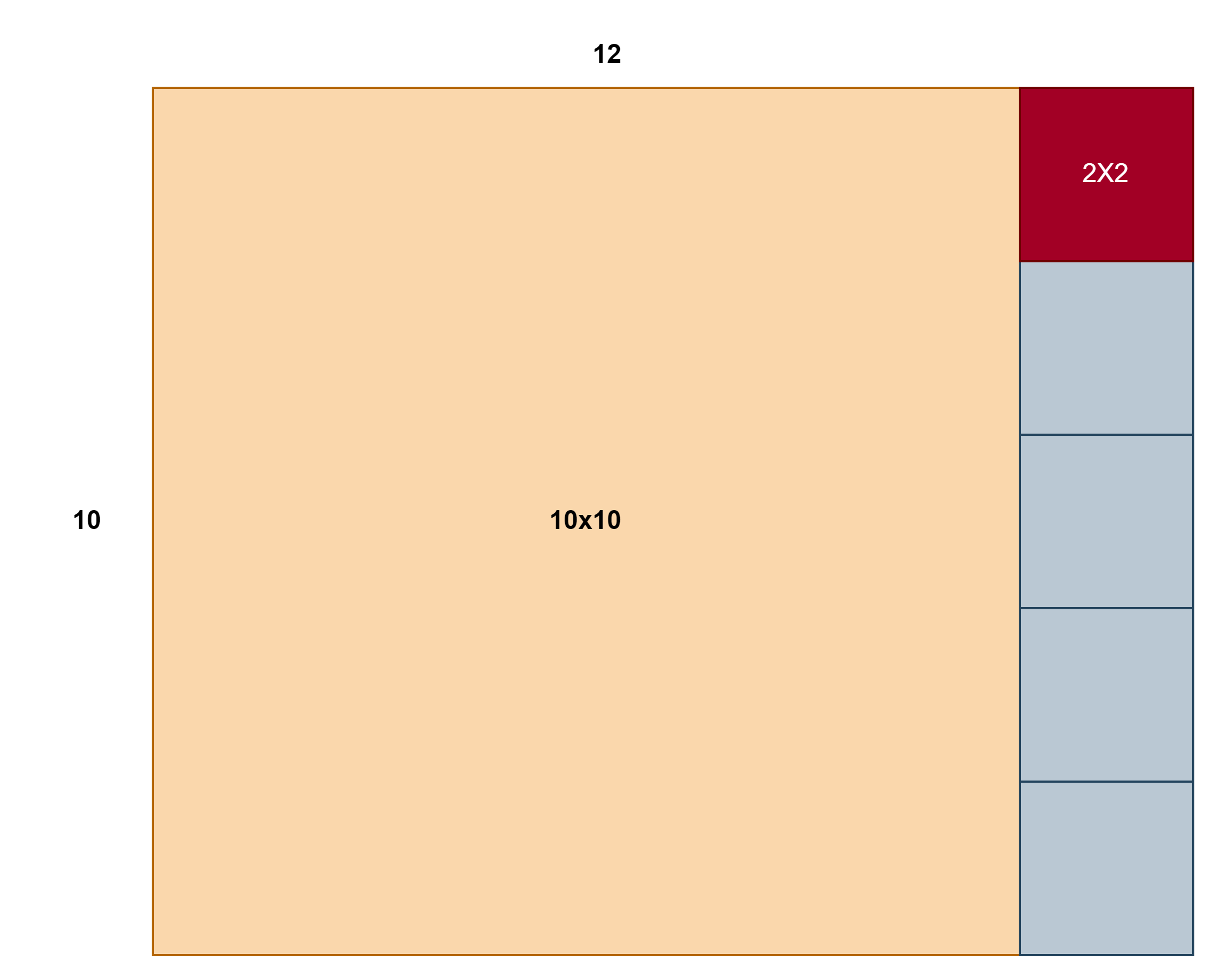
以上图形化证明过程的代码表达如下,设初始两个自然数为a,b, 并且a>b,b非0,可以证明存在两个唯一的整数 q 和 r,满足 a = q*b + r , q 为整数,且0 ≤ |r|< |d|。其中,q 被称为商,r 被称为余数,a,b分别被除数和除数,取余运算求取的就是这个余数r。
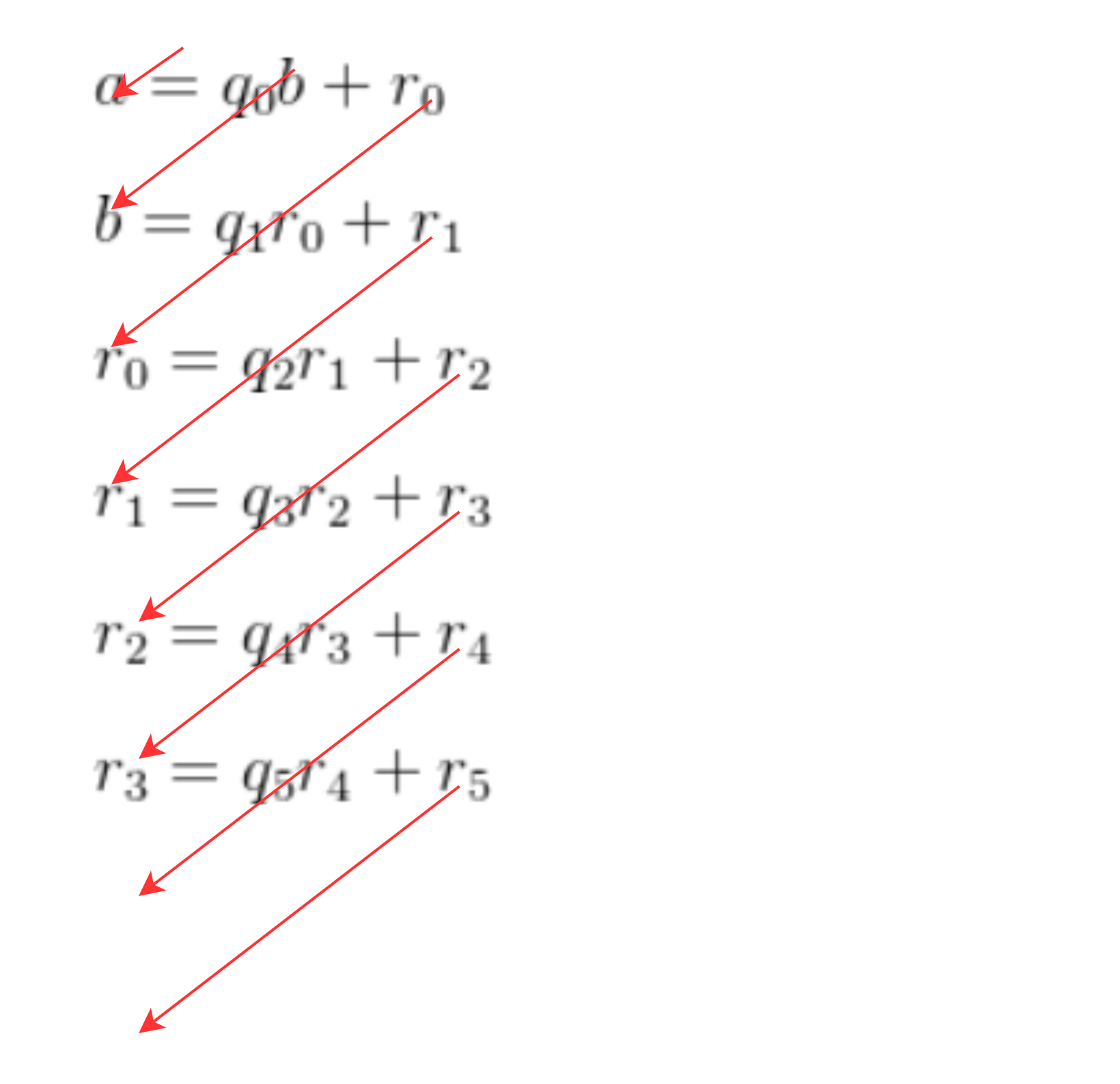
只要a,b是可公度的,这些式子不会无限列下去,从r0开始,每一步r(n+1)是r(n)的余数,r(n+1) < r(n),但是r0是自然数,起始值是有限的,所以这个过程不可能无限进行下去,最后一步总归能够整除,最后一步的除数r(n+2)就是最大公约数。
往回迭代:
.........
下一步证明,任何a,b的公度c,一定可以度量r(n+2).
由于c是公度,因此a,b都可以用它来表示,m,n为自然数
这样,上面的式子可以写成
.....
所以,r0,r1,.....r(n),r(n+1), r(n+2)都可以由c来公度,所以r(n+2)是最大公度。
以本片开头的例子为例,计算110和24的最大公约数,a=110,b=24.
a=110,b=24.
110=4*24+14.
24=1*14+10.
14=1*10+4.
10=2*4+2.
4=2*2 + 0.

定理得证。
裴蜀定理
裴蜀定理(或贝祖定理)得名于法国数学家艾蒂安·裴蜀,说明了对任何整数a ,b 和它们的最大公约数d,关于未知数x和y 的线性不定方程(称为裴蜀等式):若a ,b 是整数,且gcd( a , b ) = d gcd(a,b)=d,那么对于任意的整数x ,y , ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立,对于a,b互素的情况,一定存在x,y使的ax+by=1.
可以这样抽象理解,每次a mod b=m余r的过程,都是:
所以:
.......
也就是说,通过GCD计算最大公约数的过程,就是计算a,b线性组合的过程,系数分别为x,y:r=ax+by.
计算gcd(a,b)=ax+by所需的x,y:
......
方程是不定方程,无法限定x,y.符合要求的x,y可以构成一个一维空间,在一条直线上,但是满足x,y为整数的,并不多。另外,对于ax+by=k形式的直线,如果a,b互质,则K可以为任意整数,但是如果a,b的最小公因数大于1,则小于其最公因数的数字不能被表示。可以简单证明如下:
ax+by=k, a=nc, b=mc. 则ncx+mcy=k=>c(nx+my)=k,n,m互质,所以能表示任意整数,在乘以一个c,则只能表示sc了,s是整数。不能表示任意整数了。
假设第k层:
第k+1层:
所以:
展开:
对照第K层:
所以
并且,在最后一次的迭代中,一定是
,编程得到:
#include<stdio.h>
#include<stdlib.h>//注意,a,b必须互质!
int ex_gcd(int a, int b, int *x, int *y)
{ int x1, y1, r;if(b == 0) {if(a!= 1) {printf("%s line %d, error, a %d is not 1 in last recursive.\n", __func__, __LINE__, a);exit(-1);}*x = 1;*y = 0;return a;}r = ex_gcd(b, a % b, &x1, &y1);*y = x1 - a / b * y1; //根据推导的每层x,y的关系而来*x = y1; //同上return r;
}int main(void)
{ int a, b, x, y;while(~scanf("%d%d", &a, &b)){int ret = ex_gcd(a, b, &x, &y);printf("x : %d, y : %d, ret = %d\n", x, y, ret);//其实ret就是a,b的最大公约数printf("%d * %d + %d * %d = %d\n", a, x, b, y, a * x + b * y);}return 0;
}
下图展示了两个整数6和9的最大共因子是两个整数的线性组合的最小正整数这个事实:
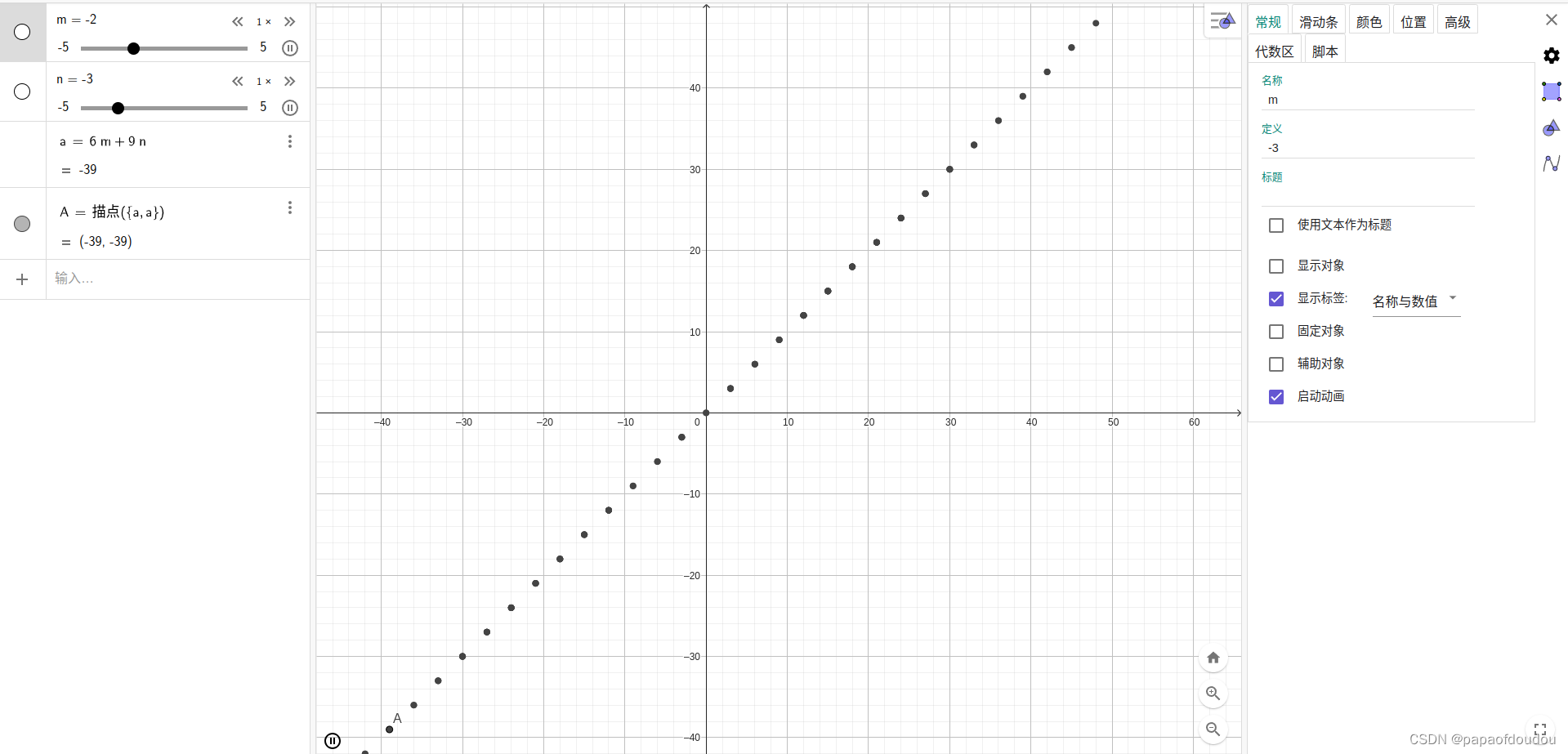
完善证明
证明过程中,依据“每次都保证余数小于除数,但是余数不可能小于0,由于起始值是有限的,所以最终算法一定会停止” 为什么不会出现无限接近0但是不为0的情况,算法为什么一定会停止呢?a,b可公度这一前提到底保证了什么?
可以利用自然数的良序原理(well-ordering principle)说明欧几里得算法一定会终止,最小数原理是自然数所具有的一种基本性质,即任何非空的自然数集中都有最小的自然数,该原理可以推广到整数集,有理数集。完整表达是:
良序原理指出,自然数集的每个非空子集都有个最小元素,即自然数在其标准的大小关系下构成一良序集。
参考资料
无理数存在性的几何证明-CSDN博客
初等数论中整除性规律证明-CSDN博客
欧几里得定理的证明-CSDN博客
初等数学的整除性规律证明-CSDN博客
[深入浅出C语言]理解取整、取余和取模 - 知乎
https://zh.wikipedia.org/wiki/%E7%AE%97%E6%9C%AF%E5%9F%BA%E6%9C%AC%E5%AE%9A%E7%90%86
结束
这篇关于图解辗转相除法(欧几里得算法)求解最大公约/最小公倍数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!