时间平均思想在电流源整流器中的应用—

时间平均思想在电流源整流器中的应用——求解基本矢量的占空比

本文主要是介绍时间平均思想在电流源整流器中的应用——求解基本矢量的占空比，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 引言

电流源型整流器和电压源型整流器的SVPWM调制的思想是类似的，只是开关状态不同，导致基本矢量的分布不同而已。本文以电流源整流器为例对基本矢量的占空比求解思路进行分析。

2. 直流侧为恒流源

下图为三相电流源型整流器的拓扑，一共是12个开关管，以六个双向开关管组成，直流侧为恒流源 $I_L$ 。
在这里插入图片描述
该变换器的开关状态表如下：

以第一扇区为例，基本矢量的占空比求解思路如下，利用正弦定理，即可求出两个基本矢量的占空比：

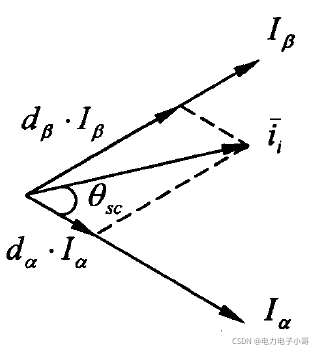
计算结果如下：

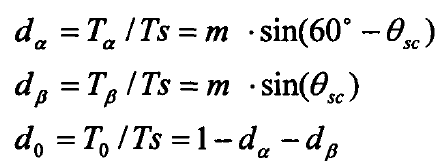
这种方法将三相的电流瞬时值信息转化为两相的电流矢量信息，然后通过数学几何的思路求解基本矢量的占空比。然而，这种方法是一种通用的方法吗？

3. 直流侧为变化的电流源

下图是一个三相隔离型矩阵整流器，前级3-1MC是一个电流源型整流器，由于变压器要满足伏秒平衡，电流要交变的。因此，变压器漏感电流 $i_L$ 是变化的，如下面的波形图所示。
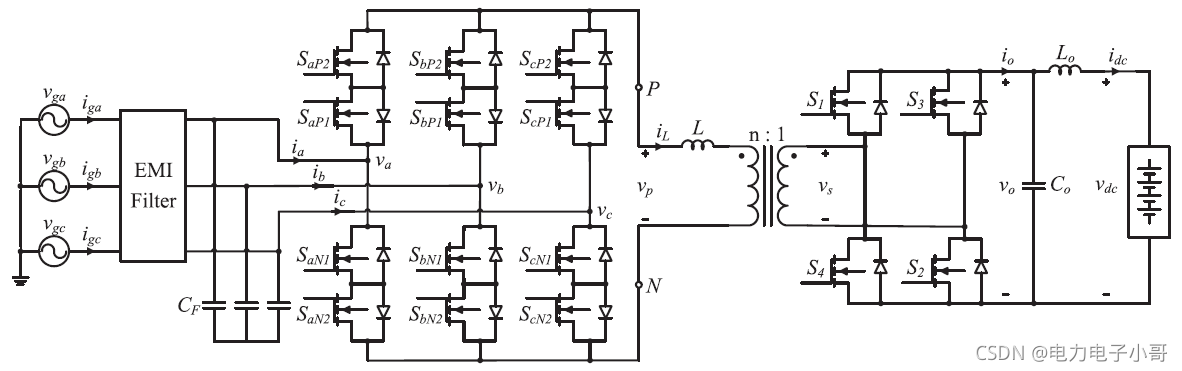
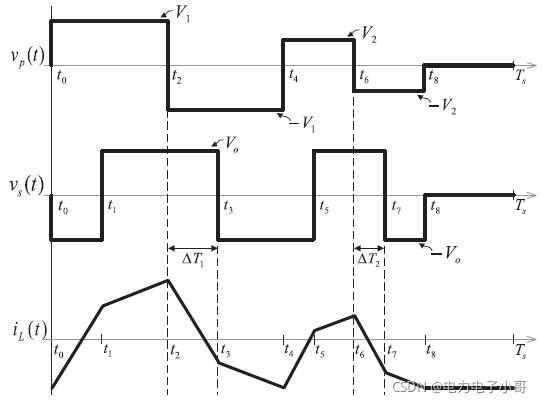
在这里插入图片描述

这种情况下，上面的分析方法就失效了，因为在一个开关周期内，直流侧的电流源是变化的，导致基本电流矢量是变化的，而上面的分析方法是把基本电流矢量当做是恒定的，因此不适用直流侧电流变化的场合。
作者提供的思路是先把一个开关周期内的三相电流的平均值求出来，然后和参考的三相电流等效。这其实就是面积等效原理，或者说是时间平均的思想，在此仅附上作者提供的运算思路、
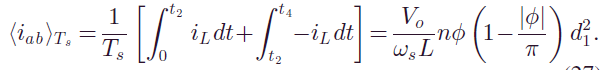
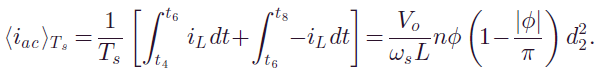
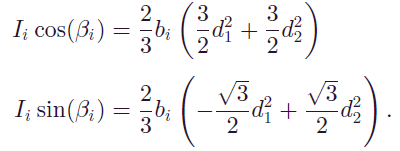
在这里插入图片描述

4. 时间平均等效思想的应用

4.1 Buck电路的时间平均思想

时间平均思想在基本的DC-DC电路中的应用很广泛，可以参考西南交通大学的许建平老师的著作。下面金逸Buck电路举例分析：
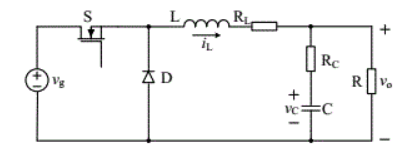
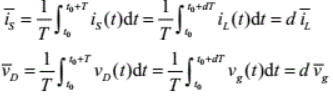
在这里插入图片描述

从表达式中可以看出，一个电流在你哥开关周期的平均值其实就是类似于分时间端的定积分，再除以总的时间，这种思想就是面积等效原理。

4.2 矩阵型整流器的时间平均思想

具体的推导过程如下图所示，第一步就是瞬时值的时间平均，这种方法在绝大部分的场合都能应用；第二步是将瞬时值进行Clark变换，结果是电流矢量的积分；第三步是最重要的，如果在一个开关周期内基本电流矢量是恒定的，就可以提取出来，但如果不是恒定的，就不能推导到下一步。所以说第三步就是决定能不能用几何关系去求解d1，d2和d0的关键。
请添加图片描述
当然，用时间平均的思想去求解恒流源模式下的d1，d2和d0也是完全没问题的，计算结果如下图所示。
在这里插入图片描述

5. 参考文献

[1]. AC-DC矩阵变换器及其应用研究
[2]. 开关变换器的时间平均等效电路建模
[3]. Modulation Strategy for a Single-StageBidirectional and Isolated AC-DC MatrixConverter for Eneray Storage Systems