波束形成基于不等式惩罚项约束与自由度限制的稳健自适应波束形成算法

本文主要是介绍波束形成基于不等式惩罚项约束与自由度限制的稳健自适应波束形成算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

这篇文章是一篇典型的基于凸优化的稳健自适应波束形成算法。作者的核心思想主要是通过惩罚约束自由度与不等式项约束不确定域从而达到阵列的稳健性，同时考虑了导向矢量失配、阵列自由度限制与协方差矩阵失真三个因素。虽然很早就打算尝试对这篇文章进行仿真，但是囿于能力问题还是没能成功，现在回过头来打算再仔细看看，对作者的内容进行补充。

阵列稳健性之导向矢量适配

针对导向矢量失配问题，作者提出了以下约束：

定义1

给定先验角度 $\theta$ ，与该角度对应的真实导向矢量 $\textbf{a}_\theta$ ，则有以下约束成立：

$|\textbf{w}^H\textbf{a}_{\theta}-1|+\delta\|\textbf{w}\|\leq c_{\theta}$

其中 $c_{\theta} \geq 0$ 为人为定义的误差阈值， $\delta \geq 0$ 为针对导向矢量失配的稳健性系数。已知在导向矢量失配问题存在的情况下，真实导向矢量可分解为其名义分量与阵列误差分量，即：

$\textbf{a}_{\theta}=\bar{\textbf{a}}_{\theta}+\Delta\textbf{a}_{\theta}$

其中 $\bar{\textbf{a}}_{\theta}$ 为其名义导向矢量分量， $\Delta\textbf{a}_{\theta}$ 为阵列误差分量，且有 $\|\Delta\textbf{a}_\theta\|\leq\delta$ 成立。

MVDR的等价优化形式可表示为：

$\min_{\mathbf{w}} \mathbf{w}^H\mathbf{R}_{i+n}\mathbf{w}~~~~s.t.~~\mathbf{w}^H\mathbf{a}_{\theta_0} = 1$

对于该最优解，与 $\mathbf{a}_{\theta}$ 邻域内的导向矢量 ${\mathbf{\bar{a}}}_{\theta}$ ，有：

$|\mathbf{w}^H\mathbf{\bar{a}}_\theta-1|\leq\max\limits_{\|\Delta\textbf{a}_\theta\|\leq\delta}|\textbf{w}^H(\textbf{a}_\theta-\Delta\textbf{a}_\theta)-~1|=~\max\limits_{\|\Delta\textbf{a}_\theta\|\leq\delta}\left|\textbf{w}^H\textbf{a}_\theta-1-\textbf{w}^H\Delta\textbf{a}_\theta\right|\\=\big|\mathbf{w}^{H}\mathbf{a}_{\theta}-1+\mathbf{e}^{j\phi}\max_{\|\Delta\textbf{a}_\theta\|\leq\delta}|\mathbf{w}^H\Delta\mathbf{a}_{\theta}|\big| =~|\mathbf{w}^H\mathbf{a}_\theta-~1|+~\max_{\|\Delta\mathbf{a}_\theta\|\leq\delta}|\mathbf{w}^H\Delta\mathbf{a}_\theta|\\=\lvert\mathbf{w}^H\mathbf{a}_\theta-1\rvert+\delta\lVert\mathbf{w}\rVert\leq\mathbf{c}_\theta,~~\forall \theta \in \Theta$

其中 $\Theta$ 为一预先定义的不确定角度域。

阵列稳健性之协方差矩阵失真

针对小快拍数下协方差矩阵的失真问题，常见的方法是根据有限的快拍数进行协方差矩阵重建，尽量得到无失真情况下的协方差矩阵；另一种方法则是根据先验角度信息对干扰域邻域范围内的导向矢量都施加约束以进行抑制，避开协方差矩阵的进一步处理过程；此处作者提出的方法明显是属于后一种。

定义2

对干扰域角度的约束可表示为：

$|\mathbf{w}^H\mathbf{a}_\phi|+\delta\|\mathbf{w}\|\leq c_\phi,\forall\phi\in\Phi_k,\forall k$

其中 $\Phi_k$ 为一根据第 $k$ 个角度的先验信息而定义的离散角度集合，同时 $c_\phi$ 表示着其抑制程度，同样的，对于该阵列权向量的最优解，与 $\mathbf{{a}}_{\phi}$ 邻域内的导向矢量 $\mathbf{\bar{a}}_{\phi}$ ,有：

$|\mathbf{w}^H\mathbf{\bar{a}}_\phi|\leq \max\limits_{\|\Delta\textbf{a}_\phi\|\leq\delta}|\textbf{w}^H(\textbf{a}_\phi-\Delta\textbf{a}_\phi)|=\max\limits_{\|\Delta\textbf{a}_\phi\|\leq\delta}|\textbf{w}^H\textbf{a}_\phi-\textbf{w}^H\Delta\textbf{a}_\phi|\\=\big|\mathbf{w}^{H}\mathbf{a}_{\phi}+\mathbf{e}^{j\theta}\max_{\|\Delta\textbf{a}_\phi\|\leq\delta}|\mathbf{w}^H\Delta\mathbf{a}_{\phi}|\big|=~|\mathbf{w}^H\mathbf{a}_\theta-~1|+~\max_{\|\Delta\mathbf{a}_\theta\|\leq\delta}|\mathbf{w}^H\Delta\mathbf{a}_\theta|\\=\lvert\mathbf{w}^H\mathbf{a}_\phi-1\rvert+\delta\lVert\mathbf{w}\rVert\leq\mathbf{c}_\phi,~~\forall \phi \in \Phi_k$

可发现，作者采取的是对波束形成器的空域响应施加约束以提高阵列稳健性。

阵列稳健性之有限自由度分配

针对阵列有限的自由度及干扰的抑制，作者在干扰域的约束问题上进一步添加了惩罚项，通过降低干扰域空域响应的最大值进行整体抑制，即：

$\min\limits_{\mathbf{w},\mathbf{\epsilon}}\max\{\gamma_k\epsilon_k\}+...~~~~ \text{s.t.}|\mathbf{w}^H\mathbf{a}_\phi|+\delta\|\mathbf{w}\|\le\epsilon_k c_\phi,\forall\phi\in\Phi_k,\forall k,~~~~...$

其中 $\gamma_k$ 为一预先指定的干扰抑制参数，更大的 $\gamma_k$ 表明该干扰源更应优先抑制，故 $\gamma_k$ 应与干扰源功率呈正相关的关系； $\mathbf{\epsilon } =\left ( \epsilon _1,\epsilon _2,...,\epsilon _k \right ) \in \mathbb{R}^K$ 为一控制空域响应的参数，在 $\gamma_k$ 的控制与max的约束下，大的 $\gamma_k$ 总会有小的 $\epsilon _k$ 与之对应，随之而来的便是对应方向上更为严格的空域响应约束；当 $\{\epsilon _k\}$ 足够大时， $\mathbf{w}$ 便总能存在一最优解。(私以为该部分与其说是自由度分配不如说是空域谱控制)

P-ICMV的优化问题约束形式

考虑了以上三种情况下不同的优化问题与约束问题，作者提出的波束形成器可表示为：

$\min_{\mathbf{w},\mathbf{\epsilon}}\mathbf{w}^H\mathbf{R}\mathbf{w}+\mu\max_k\{\gamma_k\epsilon_k\}\\ s.t.\left|\mathbf{w}^H\mathbf{a}_\theta-1\right|+\delta\left\|\mathbf{w}\right\|\leq c_\theta,\forall\theta\in~\Theta, |\mathbf{w}^H\mathbf{a}_\phi|+~\delta\left\|\mathbf{w}\right\|\leq~\epsilon_k c_\phi.\forall\phi\in~\Phi_k.\forall k$

定义3

令 $\textbf{A}\in\mathbb{C}^{M\times|\Theta|}$ 为一由期望信号邻域(该邻域应足够小)内的离散角度点的集合中的元素对应的名义导向矢量 $\boldsymbol{a}_{\theta},\forall\theta\in\Theta$ 拼接而成的阵列流型，假定 $\textbf{A}$ 的列秩为该集合中的元素个数，(此处可得采样点数显然小于阵元数)则若 $\delta\leq\min _\theta c_\theta/\sqrt{\mathbf{1}^H(\mathbf{A}^H\mathbf{A})^{-1}\mathbf{1}}$ ，P-ICMV的优化问题总是可行的。

证明如下：

考虑对于一权向量 $\mathbf{w}$ ，其相对于阵列流型而得到空域响应复向量 $\textbf{b} \in \mathbb{C}^{|\Theta|}$ ，则可通过该空域响应复向量，用最小二乘法得到 $\mathbf{w}$ 的最小二乘解，有：

$\textbf{A}^H\textbf{w}=\textbf{b}\Rightarrow \textbf{w}^*=\textbf{A}(\textbf{A}^H\textbf{A})^{-1}\textbf{b}\Rightarrow \|\textbf{w}^*\|^2=\textbf{w}^{*H}\textbf{w}^{*}\\=\textbf{w}^{*H}\textbf{A}(\textbf{A}^H\textbf{A})^{-1}\textbf{b}=\textbf{b}^{H}(\textbf{A}^H\textbf{A})^{-1}\textbf{b}\Rightarrow ~\|\textbf{w}^*\|=~\sqrt{\textbf{b}^{H}(\textbf{A}^H\textbf{A})^{-1}\textbf{b}}$

带入约束问题中的第一个约束项，有

$|b_{\theta}-1|+\delta\sqrt{\textbf{b}^H(\textbf{A}^H\textbf{A})^{-1}\textbf{b}}\leq c_\theta,\forall\theta\in\Theta$

令 $\textbf{b} = \textbf{1}$ ，即得

$\delta\le\min_\theta c_\theta/\sqrt{\textbf{1}^H(\textbf{A}^H\textbf{A})^{-1}\textbf{1}}$

该波束形成器还具有以下性质：

有限空域响应

针对 $\|\Delta\textbf{a}_\theta\|\leq\delta_\theta$ 的情况，即误差在 $\delta$ 允许的范围内时，针对P-ICMV波束形成器的可行解 $(\textbf{w},\mathbf{\epsilon})$ ，其期望信号邻域内角度的阵列响应存在一个上确界与下确界，即：

$1-{c}_\theta\le|\textbf{w}^H\mathbf{a}_\theta|\le1+ {c}_\theta,\forall\theta\in\Theta$

同样的，干扰信号邻域内角度的阵列响应也存在一个上确界：

$|\textbf{w}^H\textbf{a}_{\phi}|\leq\epsilon_k c_\phi,\forall\phi\in\Phi_k$

若进一步考虑导向矢量失配的情况，则有 $\|\Delta\textbf{a}_\theta\|\leq\delta_\theta$ ，或 $\|\Delta\textbf{a}_\theta\|\leq\max\{\delta_\theta\}$

自由度分配(过载情况下信号抑制的优先级)

P-ICMV波束形成器的优化项中，在 $\gamma_k$ 的控制与max的约束下使得波束形成器能够根据提供的 $\gamma_k$ 对对应方向上的信号进行进一步约束。

P-ICMV的优化问题约束形式对应的ADMM解

因P-ICMV的优化问题中存在一个min-max的优化项难以处理，因此作者在此进行了一个等价变换：

$\min_{\textbf{w},t,y} \textbf{w}^H\textbf{Rw}+\mu t\\s.t.|\textbf{w}^H\textbf{a}_\theta-1|+\delta\textbf{y}\leq C_\theta,\forall\theta\in~\Theta,|\textbf{w}^H\textbf{a}_\phi|+~\delta y\leq ~t c_\phi/\gamma_k,\forall\phi\in~\Phi_k,\forall k,\|\textbf{w}||\leq~ y$

显然此为一松弛操作，考虑：

$\min\max_k \mu\{ \gamma_k\epsilon_k \} ~~~~s.t. \epsilon_k \geq(|\mathbf{w}^H\mathbf{a}_\phi|+~\delta\left\|\mathbf{w}\right\|)/ c_\phi.\forall\phi\in~\Phi_k.\forall k$

该优化问题的最优值显然由 $\gamma_k$ 确定的前提下，最小化序列最大值的过程中最先到达下确界的 $\epsilon_k$ 决定，当某一个 $\epsilon_k$ 达到下确界时最优值即给出。(e.g.)

$\min \max\{ 3a,2b,7c,9d \}~~s.t.a \geq 4,b\geq3,c\geq2,d\geq1 \\\min t~~ s.t.t/3\geq4,t/2\geq3,t/7\geq2,t/9\geq1$

因此，以下优化问题的可行域显然比min-max问题的可行域更为严格。

$\min t ~~~~s.t. t \geq\gamma_k(|\mathbf{w}^H\mathbf{a}_\phi|+~\delta\left\|\mathbf{w}\right\|)/ c_\phi.\forall\phi\in~\Phi_k.\forall k$

同时，进一步引入辅助变量 $\{y_\theta,z_\theta\}$ 与 $\{y_\phi,z_\phi\}$ ，有：

$y_\theta=y,z_\theta=\textbf{w}^H\textbf{a}_\theta,y_\phi=y,z_\phi=\textbf{w}^H\textbf{a}_\phi,\forall\theta\in\Theta,\forall\phi\in\Phi_k,\forall k$

则原问题可进一步转化为：

$\min\textbf{w}^H\textbf{Rw}+\mu t\\ s.t.|z_\theta-1|+\delta y_\theta\leq c_\theta,\forall\theta\in\Theta,|z_\phi|+\delta y_\phi\leq t c_\phi/\gamma_k,\forall\phi\in\Phi_k,\forall k,\\ \|\textbf{w}\|\leq y,y_\theta=y,z_\theta=\textbf{w}^H\textbf{a}_\theta,y_\phi=~y,z_\phi=~\textbf{w}^H\textbf{a}_\phi,\forall\theta\in~\Theta,\forall\phi\in~\Phi_k,\forall k$

则可得到该问题的增广拉格朗日式为：

$L_\rho(\textbf{w},y,\{y_\theta,z_\theta\},t,\{y_\phi,z_\phi\},\{\eta_\theta,\lambda_\theta\},\{\eta_\phi,\lambda_\phi\})\\=\textbf{w}^H\textbf{R}\textbf{w}+\mu t+\sum\limits_{\theta\in\Theta}\left[\textbf{Re}\{\lambda_\theta^H(\textbf{w}^H\textbf{a}_\theta-z_\theta)\}+\frac{\rho}{2}|\textbf{w}^H\textbf{a}_\theta-z_\theta|^2\right]+~\sum\limits_{\theta\in\Theta}\left[\eta_\theta(y-y_\theta)+\frac{\rho}{2}(y-y_\theta)^2\right]\\+\sum_k\sum_{\phi\in\Phi_k}\left[\text{Re}\{\lambda_\phi^H(\mathbf{w}^H\mathbf{a}_\phi-z_\phi)\}+\frac{\rho}{2}|\mathbf{w}^H\mathbf{a}_\phi-z_\phi|^2\right]+~\sum_k\sum_{\phi\in\Phi_k}\bigg[\eta_\phi(y-~y_\phi)+~\frac{\rho}{2}(y-~y_\phi)^2\bigg]$

需要注意的是，复值优化问题，乘子与约束的内积是需要取实部的。(第一遍看这个问题的ADMM解法的时候本人也感到疑惑，到后面才发现作者是将约束15.a与约束15.b带到后面的拉格朗日乘子最小的环节，使之从一个无约束问题变化为了一个带约束问题，个人感觉这块处理得非常精妙。(可能是本人知识浅薄))

该增广拉格朗日乘子中各变量的迭代式为：

$\mathbf{x}_1^{r+1}=\arg\min\limits_{\|\textbf{w}\|\leq y}L_\rho(\mathbf{x}_1,\mathbf{x}_2^r,\mathbf{x}_3^r,\boldsymbol{\lambda}^r)$
$\textbf{x}_2^{r+1}=\operatorname{arg}\min\limits_{|z_\theta-1|+\delta y_\theta\leq c_\theta}L_{\rho}(\textbf{x}_1^{r+1},\textbf{x}_2,\textbf{x}_3^r,\boldsymbol{\lambda}^r)$
$\textbf{x}_3^{r+1}=\text{arg}\min\limits_{|z_\phi|+\delta y_\phi\leq t c_\phi/\gamma_k}L_{\rho}(\textbf{x}_1^{r+1},\textbf{x}_2^{r+1},\textbf{x}_3,\boldsymbol{\lambda}^r)$
$\lambda_\theta^{r+1}=\lambda_\theta^r+\rho(\textbf{w}^H\textbf{a}_\theta-z_\theta^{r+1}),\theta\in\Theta$
$\eta_\theta^{r+1}=\eta_\theta^r+\rho(y^{r+1}-y_\theta^{r+1}),\theta\in\Theta$
$\lambda_{\phi}^{r+1}=\lambda_{\phi}^{r}+\rho(\textbf{w}^H\textbf{a}_{\phi}-Z_{\phi}^{r+1}),\phi\in\Phi_{k},\forall k$
$\eta^{r+1}_\phi=\eta^r_\phi+\rho(y^{r+1}-y^{r+1}_\phi),\phi\in\Phi_k,\forall k$

其中 $\textbf{x}_1\triangleq(\textbf{w},y)$ ， $\textbf{x}_2\triangleq(\{y_\theta,z_\theta\})$ ， $\textbf{x}_3\triangleq(t,\{y_\phi,z_\phi\})$ ， $\boldsymbol{\lambda}=(\{\eta_\theta,\lambda_\theta\},\{\eta_\phi,\lambda_\phi\})$

定义4

在定义3成立的前提下，ADMM各变量的迭代式会收敛至最优解。

ADMM中第一个变量迭代式的解

除去增广拉格朗日函数中 $\textbf{x}_1$ 无关的分量后，求解关于 $\textbf{x}_1$ 的最优值的优化问题如下所示：

$\min\limits_{\mathbf{w}}\mathbf{w}^H\mathbf{A}\mathbf{w}+\mathrm{Re}\{\mathbf{b}^H\mathbf{w}\}+\alpha y^2+\beta y,s.t.\|\mathbf{w}\|\leq y$

其中：

$\textbf{A}=\textbf{R}+\frac{\rho}{2}(\sum\limits_{\theta\in\Theta}\textbf{a}_\theta\textbf{a}_\theta^H+\sum\limits_{k}\sum\limits_{\phi\in\boldsymbol{\Phi}_k}\textbf{a}_\phi\textbf{a}_\phi^H)$

$\textbf{b}=-\frac{1}{2}[\sum_{\theta\in\Theta}(\lambda_\theta^H\textbf{a}_\theta-\rho z_\theta^H\textbf{a}_\theta)+\sum_k\sum_{\phi\in\Phi_k}(\lambda_\phi^H\textbf{a}_\phi-\rho z_\phi^H\textbf{a}_\phi)]$

$\alpha=(|\Theta|+\sum_k|\Phi_k|)\frac{\rho}{2},\beta=\sum_{\theta\in\Theta}\eta_\theta-\rho y_\theta+\sum_k\sum_{\phi\in\Phi_k}\eta_\phi-\rho y_\phi$

则该优化问题的最优解为：

$\begin{cases}y^*=0,\mathbf{w}^*=\mathbf{0},\text{if}\beta\geq\|\mathbf{b}\|,\\ y^*=-\frac{\beta}{2\alpha},\mathbf{w}^*=\mathbf{w}(y^*),\text{if}\beta<\|\mathbf{b}\|,\|\mathbf{A}^{-1}\mathbf{b}\|\leq-\frac{\beta}{\alpha},\\ f(y^*)=1,\mathbf{w}^*=\mathbf{w}(y^*),\text{otherwise,}\end{cases}$

其中 $\mathbf{A} = \mathbf{U}\mathbf{\Lambda}\mathbf{U}^H$ ， $\textbf{w}(y)=-\textbf{U}^H\bigg[2\mathbf{\Lambda}+(2\alpha+\frac{\beta}{y})\textbf{I}\bigg]^{-1}\textbf{U}\textbf{b}$ 。

过程如下：

从 $\mathbf{A}$ 的等式可得，该矩阵为一正定阵，因此首先对该矩阵作特征分解，有： $\mathbf{A} = \mathbf{U}\mathbf{\Lambda}\mathbf{U}^H$ ；根据正交矩阵的性质，有： $\|\mathbf{\bar{w}}\|=\|\mathbf{U}^H\mathbf{w}\|=\|\mathbf{w}\|$ ，则令 $\bar{\mathbf{b}} = \mathbf{Ub}$ ，故原问题可表示为：

$\min\limits_{\mathbf{\bar{w}}}\quad\mathbf{\bar{w}}^H\mathbf{\Lambda}\mathbf{\bar{w}}+\mathrm{Re}\{\mathbf{\bar{b}}^H\mathbf{\bar{w}}\}+\alpha y^2+\beta y, s.t.|\mathbf{\bar{w}}\|\leq y$

显然该问题的最优解与关于 $\textbf{x}_1$ 的最优值的优化问题的最优解可相互转换，则其拉格朗日乘子如下：

$L(\mathbf{\bar{w}},y,\lambda)=\mathbf{\bar{w}}^H\mathbf{\Lambda}\mathbf{\bar{w}}+\mathrm{Re}\{\mathbf{\bar{b}}^H\mathbf{\bar{w}}\}+\alpha y^2+\beta y+\lambda(\|\mathbf{\bar{w}}\|-y)$

又因为 $\frac{\partial \|\mathbf{\bar{w}}\|}{\partial \mathbf{\bar{w}}}=\frac{\mathbf{\bar{w}}}{\|\mathbf{\bar{w}}\|}$ ，注意到该式在 $\|\mathbf{\bar{w}}\|=0$ 处不可导，则需对可行域进行进一步划分。

定义6

关于 $\textbf{x}_1$ 的最优值的优化问题的等价问题的最优解为 $(\mathbf{0},0)$ ，当且仅当 $\beta\geq\|\mathbf{\bar{b}}\|$ 。

证明如下：

$\beta\geq\|\mathbf{\bar{b}}\|\Rightarrow f(\mathbf{0},0) \quad optimal$

已知 $\|\mathbf{\bar{w}}\|=\mathbf{\bar{w}}\frac{\partial \|\mathbf{\bar{w}}\|}{\partial \mathbf{\bar{w}}}=\mathbf{\bar{w}}\mathbf{\bar{w}}'=\epsilon$ ,令 $f(\mathbf{\bar{w}},y)=\mathbf{\bar{w}}^H\mathbf{\Lambda}\mathbf{\bar{w}}+\mathrm{Re}\{\mathbf{\bar{b}}^H\mathbf{\bar{w}}\}+\alpha y^2+\beta y$ ，则有：

$f(\bar{\textbf{w}},y) \geq f(\bar{\textbf{w}},\epsilon ) = f(\epsilon\mathbf{\bar{w}}',\epsilon)=(\mathbf{\bar{b}}^H\mathbf{\bar{w}}'/\|\mathbf{\bar{w}}\|+\beta)\epsilon+|o(\epsilon^2)| \\~~~~~~~~~~\geq(-\|\mathbf{\bar{b}}\|+\beta)\epsilon+|o(\epsilon^2)|\geq 0=f(\mathbf{0},0)$

$f(\mathbf{0},0) \quad optimal\Rightarrow \beta\geq\|\mathbf{\bar{b}}\|$

假定 $\beta<\|\mathbf{\bar{b}}\|$ ，定义一可行解为 $(-\epsilon\mathbf{\bar{b}}/\|\mathbf{\bar{w}}\|,\epsilon),\epsilon > 0$ ，有：

$f(-\epsilon\mathbf{\bar{b}}/\|\mathbf{\bar{w}}\|,\epsilon)=(-\|\mathbf{\bar{b}}\|+\beta) \epsilon + |o(\epsilon^2)| \leq0$

则 $\beta\geq\|\mathbf{\bar{b}}\|$ 。

因此为了避开最优解为 $(\mathbf{0},0)$ 的情况，首先考虑 $\beta<\|\mathbf{\bar{b}}\|$ 的条件。在 $\beta<\|\mathbf{\bar{b}}\|$ 下该问题的KKT条件为：

$\|\mathbf{\bar{w}}\|\leq y$
$\lambda \geq 0$
$\lambda(\|\mathbf{\bar{w}}\|-y)=0$
$\frac{\partial L(\mathbf{\bar{w}},y,\lambda)}{\mathbf{\partial \bar{w}}}=2\mathbf{\Lambda}\mathbf{\bar{w}}+\mathbf{\bar{b}}+\lambda\frac{\mathbf{\bar{w}}}{\|\mathbf{\bar{w}}\|}=\mathbf{0}$
$\frac{\partial L(\mathbf{\bar{w}},y,\lambda)}{\partial y}=2\alpha y + \beta - \lambda = 0$

当 $\lambda = 0$ 时，根据4.可得： $\mathbf{\bar{w}} = -\frac{1}{2}\mathbf{\Lambda}^{-1}\mathbf{\bar{b}}$ ，根据5.可得： $y=-\frac{\beta}{2\alpha}$ ，当 $\|\mathbf{\Lambda}^{-1}\mathbf{\bar{b}}\|\leq-\frac{\beta}{\alpha}$ 时1.成立。

当 $\lambda > 0$ 时，根据3.可得 $\|\mathbf{\bar{w}}\|=y$ ，根据5.可得 $\lambda = 2\alpha y + \beta$ ，带入4.即得：

$\mathbf{\bar{w}}_i=-\frac{\mathbf{\bar{b}}_iy}{2\lambda_iy+2\alpha y+\beta},\forall i,-\frac{\beta}{2\alpha}\le y=\|\mathbf{\bar{w}}\|$

$\mathbf{\bar{w}}=-\left[2\mathbf{\Lambda}+(2\alpha+\frac{\beta}{y})\mathbf{I}\right]^{-1}\mathbf{\bar{b}}$

$\mathbf{w}=-\mathbf{U}^H\left[2\mathbf{\Lambda}+(2\alpha+\frac{\beta}{y})\mathbf{I}\right]^{-1}\mathbf{Ub}$

$y\ge\max\{0,-\frac{\beta}{2\alpha}\} = y_{\min}$

从上式可得：

$y=\sqrt{\sum _{i=1}^{M}{\mathbf{\bar{w}}_i^2}}\Rightarrow 1= \sum\limits_{i=1}^M\frac{|\bar{\mathbf{b}}_i|^2}{(2\lambda_iy+2\alpha y+\beta)^2} \triangleq f(y)$

且 $f(y)$ 为单调递减。且进一步考虑 $\lambda >0$ 与 $\beta<\|\mathbf{\bar{b}}\|$ ，有： $\mathbf{\bar{w}} = -(2\mathbf{\Lambda}+\frac{\lambda}{y}\mathbf{ I})^{-1}\mathbf{\bar{b}}\Rightarrow \left \| \mathbf{\bar{w}}\right \|=~y=~\frac{\lambda-\beta}{2\alpha}=~\left \| -(2\mathbf{\Lambda}+\frac{\lambda}{y}\mathbf{ I})^{-1}\mathbf{\bar{b}}\right \| <~ \frac{1}{2}\left \| \mathbf{\Lambda}^{-1} \mathbf{\bar{b}} \right \|\Rightarrow ~\|\mathbf{\Lambda}^{-1}\mathbf{\bar{b}}\|>~-~\frac{\beta}{\alpha}$

且有：

$\left\{\begin{matrix} f(0) >1,y_{min} = 0 \\ f(-\frac{\beta}{2\alpha})>1,y_{min =-\frac{\beta}{2\alpha} } \end{matrix}\right.$

进一步验证了 $y^*>y_{{min}}$ 。同样地，考虑 $f(y^*)=1$ ，则有：

$y^*=y^*\sqrt{f(y^*)}=\sqrt{\sum_{i=1}^M\frac{|\overline{\text{b}}_i|^2}{(2\lambda_i+2\alpha+\beta/y^*)^2}}\leq~\sqrt{\sum_{i=1}^{M}\frac{|\bar{\mathbf{b}}_i|^2}{(2\lambda_i)^2}}=~\|\mathbf{\Lambda}^{-1}\bar{\mathbf{b}}\|/2\triangleq~ y_{{max}}$

即确定了 $y_{{max}}>y^*>y_{{min}}\Rightarrow y\in(\text{max}\{0,-\frac{\beta}{2\alpha}\},\|\textbf{A}^{-1}\textbf{b}\|/2])$ ，因此最优解即可得到。

ADMM中第二个变量迭代式的解

该优化问题是可分别对每对 $\{y_\theta,z_\theta\}$ 分别求解得到，该优化问题可表示为：

$\min\limits_{y_\theta,z_\theta}a_\theta|z_\theta|^2+\text{Re}\{b_\theta^H z_\theta\}+\alpha_\theta y_\theta^2+\beta_\theta y_\theta, s.t.|z_\theta-1|+\delta y_\theta\le c_\theta$

其中 $a_\theta=\alpha_\theta=\frac{\rho}{2}$ ， $b_\theta=-\lambda_\theta-\rho\textbf{w}^H\textbf{a}_\theta$ ， $\beta_\theta=-\eta_\theta-\rho y$ 。该系列的复SOCP优化问题可通过以下引理进行求解：

引理

考虑一个复SOCP优化问题为：

$\min\limits_{x,y}a|x|^2+\text{Re}\{b^Hx\}+\alpha y^2+\beta y\quad s.t.|x-d|+\delta y\leq c$

其中 $\textit{a},\alpha\in\mathbb{R}>0$ ， $\quad\text{c},\delta\in\mathbb{R}\geq\text{0}$ ， $\beta \in \mathbb{R}$ ， $\textit{b,d}\in\mathbb{C}$ ，令 $\psi =\angle (2ad+b)$ ， $r=|\frac{2ad+b}{2a}|$ ，其最优解为：

$y^*=\min\{-\frac{\beta}{2\alpha},\frac{2a\delta(c-r)-\beta}{2a\delta^2+2\alpha},c/\delta\}, x^*=d-c e^{j\psi}+e^{i\psi}\max\{c-r,\delta y^*\}$

证明如下：

由约束项得： $c-\delta y\ge0$ ，首先求解 $x^*$ ，对于任何在约束项内的 $y\leq c/\delta$ ，有：

$\min\limits_{x\in\mathbb{C}}a|x|^2+\mathrm{Re}\{b^Hx\}\quad\text{s.t.}|x-d|^2\le\bar{c}^2$

带入 $x=d$ ，显然约束项成立，因此slater条件成立，注意到 $x$ 为复数，且该问题优化函数为强凸函数，对其求偏导有点难度，因此可根据本人在前一文章中的KKT条件部分，得该凸问题的KKT条件为：

$|x-d|^2-\bar{c}^2\le0$
$\lambda\geq0$
$\lambda(|x-d|^2-\bar{c}^2)=0$
$2ax+b+2\lambda(x-d)=0$

由此可发现若 $x=d$ ，则 $2ad=-b$ ，不可确定 $\lambda$ ，因此首先考虑 $x\neq d$ 时的情况。在 $x\neq d$ 的前提下，根据4.，有：

$\lambda = -\frac{2ax + b}{2(x-d)}$

当 $\lambda>0$ 时，根据3.，有： $|x-d|^2\le\bar{c}^2\Rightarrow x=d+\bar{c}e^{j\phi}$ ，其中 $\phi \in [-\pi,\pi]$ 为转向角，带入 $\lambda$ ，有：

$\lambda = -\frac{2ax + b}{2(x-d)}=-\frac{2a(d+\bar{c}e^{j\phi})+b}{2\bar{c}e^{j\phi}}=-\frac{2ade^{-j\phi}+2a\bar{c}+b e^{-j\phi}}{2\bar{c}}$

根据2.，有： $-(2ad+b)e^{-j\phi}> 0$ ，因此可得 $e^{j\phi}=-\frac{2ad+b}{|2ad+b|}$ 。

当 $\lambda=0$ 时， $x=-\frac{b}{2a}$ ，带入1.，有： $|2ad + b| \le 2a \bar{c}$ ，因此 $x\neq d$ 的最优解为：

$x^*=\begin{cases}-\frac{b}{2a},\quad\text{if}|2ad+b|\le2a\bar{c}\\ d-\frac{2ad+b}{|2ad+b|}\bar{c},\quad\text{otherwise}\end{cases}$

将 $x=d$ 的情况包括进去，令 $\psi = \angle(2ad + b)$ (复数在复坐标轴上的角度)， $r=|\frac{2ad+b}{2a}|$ ，则有：

$e^{j\psi} = \frac{2ad+b}{\left | 2ad+b \right |}\Rightarrow -\frac{b}{2a}=d-re^{j\psi}$

$x^*=\begin{cases}d-re^{j\psi},&\text{if}r\le\bar c,\\[2ex]d-\bar c e^{j\psi},&\text{otherwise.}\end{cases}=d+~e^{j\psi}\max\{-r,-\bar{c}\}=~d-~ce^{j\psi}+~e^{j\psi}\max\{c-~r,\delta y\}$

即得 $x^*$ 。

对于 $y^*$ 的求解，将 $x^*$ 带回原式，可得：

$\min\limits_{y}f(y)\quad s.t.y\leq c/\delta$

其中：

$f(y)=a\left(\max\{c-r,\delta y\}\right)^2+2a(r-c)\max\{c-r,\delta y\}+\alpha y^2+\beta y\\=max\{ -a(c-r)^2,a\delta^2y^2-2a(c-r)\delta y\}+\alpha y^2+ \beta y$

$\partial f(y)=2a\delta^2\max\{0,y-\frac{c-r}{\delta}\}+2\alpha y+\beta$

显然 $f(y)$ 连续且强凸，因此存在两种情况：1. $y^* < c/\delta$ ，2. $y^* = c/\delta$ 。若 $\partial f(\frac{c}{\delta})=\frac{2ar+2\alpha c+\delta\beta}{\delta}\le0$ ，则 $y^*$ 在 $y\leq c/\delta$ 时单调递减，即得 $y^* = c/\delta$ 。若 $\partial f(\frac{c-r}{\delta})=2a\frac{c-r}{\delta}+\beta \geq 0$ ，则 $y^*= - \frac{\beta}{2\alpha}$ 。若非以上两种情况，则：

$f(y^*)=2a\delta^2y^*-2a\delta(c-r)+2\alpha y^*+\beta=0\Rightarrow y^*=\frac{2a\delta(c-r)-\beta}{2a\delta^2+2\alpha}$

因此有：

$y^*=\begin{cases}y_1=-\frac{\beta}{2\alpha},\quad\text{if}\lambda_1\ge0,\\ y_2=\frac{c}{\delta},\quad\text{if}\lambda_2\le0,\\ y_3=\frac{2a\delta(c-r)-\beta}{2a\delta^2+2\alpha},\quad\text{if}\lambda_1<0,\lambda_2\ge0\end{cases}$

其中 $\lambda_1 = 2 \alpha c - 2 \alpha r + \delta \beta < \lambda_2 = 2 \alpha c + 2 a r + \delta \beta$ 。注意到这三种情况下 $y^*$ 都是其最小值，因此有：

$y^*=\min\{-\frac{\beta}{2\alpha},\frac{2a\delta(c-r)-\beta}{2a\delta^2+2\alpha},c/\delta\}$

即得 $y^*$ 。

ADMM中第三个变量迭代式的解

该优化问题可表示为：

$\begin{array}{l}\min\limits_{t.\{y_\phi.z_\phi\}}\mu t+\sum\limits_{k}\sum\limits_{\phi<\Phi_k}a_\phi|z_\phi|^2+\text{Re}\{b_\phi^H z_\phi\}+\alpha_\phi y_\phi^2+\beta_\phi y_\phi\\ s.t.\quad|z_\phi|+\delta y_\phi\leq t c_\phi/\gamma_k.\forall\phi\in\Phi_k,k=1,\dots,K,\end{array}$

其中 $a_{\phi}=\alpha_{\phi}=\frac{\rho}{2}$

将该优化问题拆解为两部分，第一部分为：

$\min_{y_\phi,z_\phi}a_\phi|z_\phi|^2+\text{Re}\{b_\phi^H z_\phi\}+\alpha_\phi y_\phi^2+\beta_\phi y_\phi\quad s.t.~~|z_\phi|+\delta y_\phi\le\bar{t}c_\phi/\gamma_k$

根据上一引理，其最优解为：

$y_\phi^*=\min\left\{-\frac{\beta_\phi}{2\alpha_\phi},\frac{\delta(2a_\phi\bar{t}c_\phi/\gamma_k-|b_\phi|)-\beta_\phi}{2a_\phi\delta^2+2\alpha_\phi},\frac{\bar{t}c_\phi}{\gamma_k\delta}\right\}$

$z_\phi^*=-e^{j\psi_\phi}\text{min}\left\{\frac{|b_\phi|}{2a_\phi},\bar{t}c_\phi/\gamma_k-\delta y_\phi^*\right\}$

第二部分为一无约束问题：

$\underset{t}{\text{min}}\mu t+f(t)$

其中 $f(t) \triangleq \sum_k \sum_{\phi \in \Phi_k} f_\phi(t)$ ，且令 $g(t) = \mu t+f(t)$ ，有：

$f_\phi(t)=\begin{cases}a_{\phi,1}t^2+b_{\phi,1}t,t\le\bar{t}_{\phi,1},\\ a_{\phi,2}t^2+b_{\phi,2}t+c_{\phi,2},\bar{t}_{\phi,1}<t\le\bar{t}_{\phi,2},\\ c_{\phi,3},\bar{t}_{\phi,2}<t,\end{cases}=~\min\{a_{\phi,1}t^2+~b_{\phi,1}t,a_{\phi,2}t^2+~b_{\phi,2}t+~c_{\phi,2},c_{\phi,3}\}$ $a_{\phi,1}=\frac{\alpha_{\phi}c_{\phi}^{2}}{\gamma_{k}^{2}\delta^{2}},b_{\phi,1}=\frac{\beta_{\phi}c_{\phi}}{\gamma_{k}\delta},c_{\phi,3}=~-~\frac{b_{\phi}^{2}}{4a_{\phi}}-~\frac{\beta_{\phi}^{2}}{4\alpha_{\phi}},a_{\phi,2}=~\frac{\alpha_\phi a_\phi c_\phi^2}{\gamma_k^2(\alpha_\phi+a_\phi\delta^2)},b_{\phi,2}=~\frac{\delta a_\phi c_\phi\beta_\phi-\alpha_\phi c_\phi|b_\phi|}{\gamma_k(\alpha_\phi+a_\phi\delta^2)},\\ c_{\phi,2}=-\frac{(\delta|b_\phi|+\beta_\phi)^2}{4(\alpha_\phi+a_\phi\delta^2)},\bar{t}_{\phi,1}=-\frac{\gamma_k(|b_\phi|\delta^2+\beta_\phi\delta)}{2\alpha_\phi c_\phi},\bar{t}_{\phi,2}=-\frac{\gamma_k(\beta_\phi\delta-|b_\phi|\alpha_\phi/a_\phi)}{2\alpha_\phi c_\phi}$

则该问题的最优解可表示为：

$t^*=-\frac{\sum_k\sum_{\phi\in\Phi_k}b_{\phi,1}+\mu}{2\sum_k\sum_{\phi\in\Phi_k}a_{\phi,1}}$

其过程如下：

首先对 $f(t)$ 进行求导，有：

$\frac{\partial f(t)}{\partial t}=\sum_k\sum_{\phi\in\Phi_k}\min\{2a_{\phi,1}t+b_{\phi,1},2a_{\phi,2}t+b_{\phi,2},0\}$

$\frac{\partial ^2f(t)}{\partial t^2}=\sum_k\sum_{\phi\in\Phi_k}\min\{2a_{\phi,1},2a_{\phi,2},0\}$

显然 $\frac{\partial f(t)}{\partial t}$ 在 $t\leq\max_{\phi}\{\bar{t}_{\phi,2}\}\overset{\triangle}{=}t_{\text{max}}$ 上是单调递增且连续的，且在 $t\ge t_{\text{max}}$ 上有 $\frac{\partial f(t)}{t}=0$ ，根据一阶最优性条件：

$\frac{\partial g(t^*)}{\partial t}=0\Rightarrow \frac{\partial f(t^*)}{\partial t} = -\mu$

因此：

$t^* \leq t_{\text{max}}\Rightarrow\frac{\partial f(t^*)}{\partial t} = 2at^* + b$

若 $\frac{\partial f(t_{\text{min}})}{\partial t}>-\mu,t_{\text{min}}\overset{\Delta}{=}\min_{\phi}\{\bar{t}_{\phi,1}\}$ ，则在该可行域内的最优点为 $t_{min}$ ，有：

$a=\sum_k\sum_{\phi\in\Phi_k}a_{\phi,1},b=\sum_k\sum_{\phi\in\Phi_k}b_{\phi,1}$

若 $t_\text{min}\le t\le t_\text{max}$ ，则最优解一定在可行域内，因此将 $\{\bar{t}_{\phi,1}\}$ 与 $\{\bar{t}_{\phi,2}\}$ 中的元素重新以递增的形式拼接成一个集合 $\{\tilde{t}_\ell\}$ ，当 $\frac{\partial f(\tilde{t}_\ell)}{\partial t}\leq-\mu$ 且 $\frac{\partial f(\tilde{t}_{\ell+1})}{\partial t}\geq-\mu$ 时即得到最优解，因此有：

$a=\sum_{\phi\in\Omega_1}a_{\phi,1}+\sum_{\phi\in\Omega_2}a_{\phi,2},b=\sum_{\phi\in\Omega_1}b_{\phi,1}+\sum_{\phi\in\Omega_2}b_{\phi,2},$

其中 $\Omega_1=\{\phi|\bar{t}_{\phi,1}\ge\tilde{t}_{\ell+1}\},\Omega_2=\{\phi|\bar{t}_{\phi,1}\le\tilde{t}_\ell,\bar{t}_{\phi,2}\ge\tilde{t}_{\ell+1}\}$ ， $t^* = -\frac{b+\mu}{2a}$ 。

仿真

囿于时间原因，打算通过对文中的优化问题12.进行CVX求解权向量，部分仿真条件如表所示：

阵元数	10
信噪比	0
快拍数	100
扰噪比	20
阵元间距	半波长
信源数	1
干扰数	2
信源到达角	5°
干扰到达角	-30°，45°
信号域宽度	4°
角度误差上限	2°
角度采样步长	1°
期望信号误差控制量 $c_{\theta}$	{6,4,2,4,6}*0.1
导向矢量误差分量上确界 $\delta$	0.24
干扰信号误差控制量 $c_{\phi}$	$c_\phi=\hat{\sigma}_\phi^{-1}/\text{max}_{\phi\in\Phi_k}\{\hat{\sigma}_\phi^{-1}\}$ ， $\hat{\sigma}_\phi^2=1/\textbf{a}_\phi^H\textbf{R}^{-1}\textbf{a}_\phi$
干扰抑制优先权重 $\gamma_k$	$\gamma_k=\beta_k/\max_{k'}\{\beta_{k'}\}$ ， $\beta_k=\sum_{\phi\in\Phi_k}\hat{\sigma}_\phi^2$
噪声和干扰抑制的权衡参数 $\mu$	$10 \lambda_{max}(\mathbf{R})$

代码如下所示：

clc;
clear;
jk = 0;
snr = 0;
deg_dev_predf = 2;%%预定义的角度最大偏移量
ang_mismatch1 = randi(deg_dev_predf*2)-deg_dev_predf;
ang_mismatch2 = randi(deg_dev_predf*2)-deg_dev_predf;
ang_mismatch3 = randi(deg_dev_predf*2)-deg_dev_predf; %%三个不同方向的DOA误差
%% 初始化及设定参数
array_num = 10;%%阵元数
snapshot_num = 100;%%快拍数
source_aoa = [5,-30,45];%%信源到达角
tgt_ang = 1;
c = 340;%%波速
f = 1000;%%频率
lambda = c/f;%%波长
d = 0.5*lambda;
inr1 = 20;
inr2 = 20;
source_num = length(source_aoa);%%信源数
sig_nr = [snr,inr1,inr2];%%信号功率dBw
deg_deviate = 3;%%误差角度偏离
source_dev = source_aoa+[ang_mismatch1,ang_mismatch2,ang_mismatch3];
reco_size = 4;
reso = 1;
%% 转向矢量
a_bar = exp(-1i*(0:array_num-1)'*pi*sind((source_dev(tgt_ang))));%%实际带有误差的阵列响应矢量
A = exp(-1i*(0:array_num-1)'*2*pi*(d/lambda)*sind(source_aoa));%%阵列响应矩阵
tar_sig = wgn(1,snapshot_num,sig_nr(tgt_ang));
inf1 = wgn(1,snapshot_num,sig_nr(2));
inf2 = wgn(1,snapshot_num,sig_nr(2));
n = (randn(array_num,snapshot_num)+randn(array_num,snapshot_num)*1i)/sqrt(2);
rec_sig = A(:,1)*tar_sig+A(:,2)*inf1+A(:,3)*inf2+n;
R = rec_sig*rec_sig'/snapshot_num;%%接收阵的协方差矩阵
[U,Gamma,V] = svd(R);
Rs = A(:,1)*tar_sig*(A(:,1)*tar_sig)'/snapshot_num;
Ri = (A(:,2)*inf1+A(:,3)*inf2)*(A(:,2)*inf1+A(:,3)*inf2)'/snapshot_num;
Rn = n*n'/snapshot_num;
Us = U(:,1:source_num);
Un = U(:,source_num+1:end);
%% 算法
%%mu
para_mu = max(abs(diag(Gamma)))*10;
%%delta
para_delta = 0.24;
ds_ang_set = source_dev(1)-reco_size:reso:source_dev(1)+reco_size;
ds_sv = exp(-1i*(0:array_num-1)'*2*pi*(d/lambda)*sind(ds_ang_set));
%%c_theta
c_theta = (abs(-2*floor(length(ds_ang_set)/2):2:2*floor(length(ds_ang_set)/2))+2)*0.1;
intf_ang_set = [];
%%gamma_k and c_phi
for ik = 2:source_numintf_ang_set = [intf_ang_set,source_dev(ik)-reco_size:reso:source_dev(ik)+reco_size];
end
intf_sv = exp(-1i*(0:array_num-1)'*2*pi*(d/lambda)*sind(intf_ang_set));
c_phi = zeros(1,length(intf_ang_set));
for ik = 1:length(intf_ang_set)sv_current = intf_sv(:,ik);c_phi(ik) = sqrt(sv_current'*inv(R)*sv_current);
end
c_phi = c_phi/max(c_phi);
beta_k = zeros(1,source_num-1);
for ik = 2:source_numphi_k = source_dev(ik)-reco_size:reso:source_dev(ik)+reco_size;for jk = 1:length(phi_k)sv_current = exp(-1i*(0:array_num-1)'*2*pi*(d/lambda)*sind(phi_k(jk)));beta_k(ik-1) = beta_k(ik-1)+1/(sv_current'*inv(R)*sv_current);end
end
beta_k = beta_k/max(beta_k);
gamma_k = [];
for ik = 2:source_numgamma_k = [gamma_k,beta_k(ik-1)*ones(1,length(phi_k))];
end
c_theta_length = length(c_theta);
c_phi_length = length(c_phi);
c_phi_gamma_k = c_phi./gamma_k;
cvx_begin quietvariable w0(array_num,1) complexvariable t minimize(w0'*R*w0+para_mu*t);subject to%%constrainsts1for ik = 1:c_theta_lengthabs(w0'*ds_sv(:,ik)-1)+para_delta*norm(w0,2) <= c_theta(ik);end%%constrainsts2for ik = 1:c_phi_length(abs(c_phi_gamma_k(ik)*w0'*intf_sv(:,ik))+para_delta*norm(w0*sqrt(c_phi_gamma_k(ik)),2)) <= t;end
cvx_end
beam_plot(w0);
function [] = beam_plot(input_weight_vector)
array_num = length(input_weight_vector);
theta = -90:0.01:90;
p = exp(-1j*2*pi*(0:array_num-1)'*sind(theta)/2);
y = input_weight_vector'*p;
outputval = 20*log10(abs(y)/max(abs(y)));
for ik = 1:length(outputval)if outputval(ik) <= -100outputval(ik) = -100;end
end
figure()
plot(theta,outputval,'LineWidth',2);
end

仿真结果如下所示：

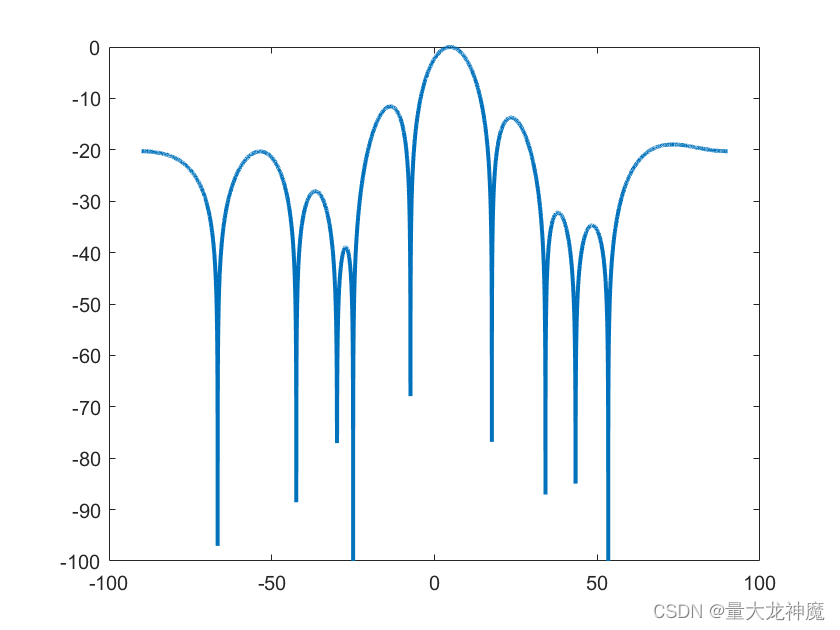
由于本次仿真只采用了10个阵元，故从波束图上不能很好地看出惩罚项的添加对干扰域信号的抑制作用(实际上可从上图模糊看出干扰角度那块的旁瓣低了不少)，该类算法还有一个痛点个人觉得便是直接通过凸优化求解权向量只能大致地对干扰域邻域内的信号进行抑制，而不能像导向矢量约束类算法那样对干扰进行精确抑制。该篇文献中对min-max问题的松弛及对优化问题15的ADMM求解是本人觉得的亮点，后者通过将难处理的约束项拉到增广拉格朗日式的最小化问题中当作约束项，一定程度上减轻了绝对值操作的处理难度。

代码可能有错，大佬们若发现问题可及时指出，谢谢。

参考文献

Wenqiang Pu, Jinjun Xiao, Tao Zhang, Zhi-Quan Luo, A penalized inequality-constrained approach for robust beamforming with DoF limitation, Signal Processing, Volume 202, 2023, 108746.

这篇关于波束形成基于不等式惩罚项约束与自由度限制的稳健自适应波束形成算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

波束形成基于不等式惩罚项约束与自由度限制的稳健自适应波束形成算法

前言

阵列稳健性之导向矢量适配

定义1

阵列稳健性之协方差矩阵失真

定义2

阵列稳健性之有限自由度分配

P-ICMV的优化问题约束形式

定义3

P-ICMV的优化问题约束形式对应的ADMM解

定义4

ADMM中第一个变量迭代式的解

定义6

ADMM中第二个变量迭代式的解

引理

ADMM中第三个变量迭代式的解

仿真

参考文献

相关文章

SpringBoot实现基于URL和IP的访问频率限制

Linux限制ip访问的解决方案

如何提高Redis服务器的最大打开文件数限制

SQL中的外键约束

不懂推荐算法也能设计推荐系统

康拓展开（hash算法中会用到）

csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

poj 3974 and hdu 3068 最长回文串的O（n）解法(Manacher算法)

波束形成 基于不等式惩罚项约束与自由度限制的稳健自适应波束形成算法

前言

阵列稳健性之导向矢量适配

定义1

阵列稳健性之协方差矩阵失真

定义2

阵列稳健性之有限自由度分配

P-ICMV的优化问题约束形式

定义3

P-ICMV的优化问题约束形式对应的ADMM解

定义4

ADMM中第一个变量迭代式的解

定义6

ADMM中第二个变量迭代式的解

引理

ADMM中第三个变量迭代式的解

仿真

参考文献

相关文章

波束形成基于不等式惩罚项约束与自由度限制的稳健自适应波束形成算法