代码随想录算法训练营第五十六天 |1143.最长公共子序列、1035.不相交的线、53. 最大子序和动态规划

本文主要是介绍代码随想录算法训练营第五十六天 |1143.最长公共子序列、1035.不相交的线、53. 最大子序和动态规划，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、1143.最长公共子序列

题目链接/文章讲解：代码随想录

视频讲解：动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列_哔哩哔哩_bilibili

思考：

1.确定dp数组（dp table）以及下标的含义

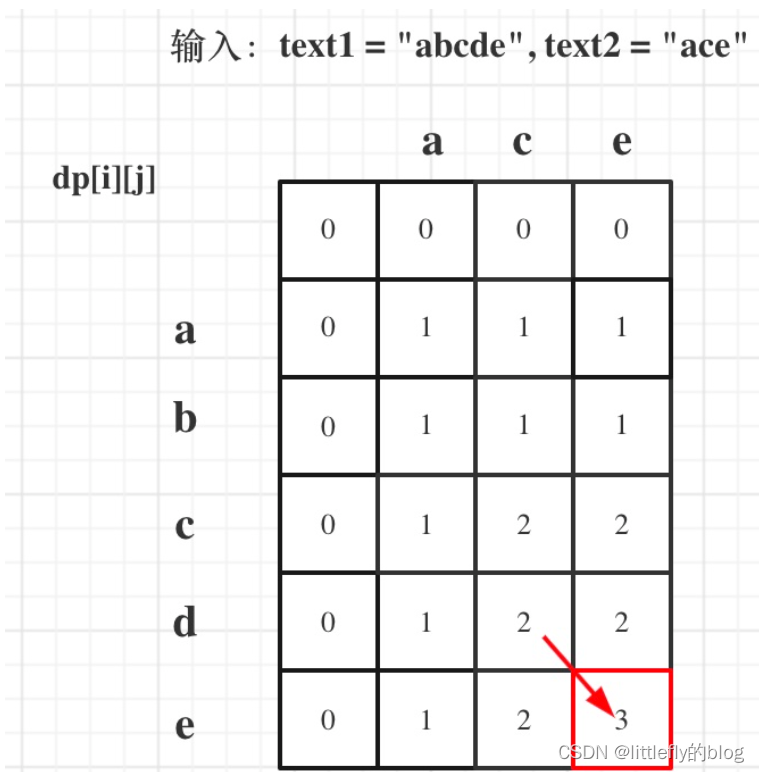
dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

2.确定递推公式

两种情况：

如果text1[i - 1]与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1]与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的

代码如下：
if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;
} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
3.dp数组的初始化

统一初始为0

4.确定遍历顺序

从前向后，从上到下

5.举例推导dp数组

代码实现：

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i - 1] == text2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[text1.size()][text2.size()];}
};

时间复杂度: O(n * m)，其中 n 和 m 分别为 text1 和 text2 的长度
空间复杂度: O(n * m)

二、1035.不相交的线

题目链接/文章讲解：代码随想录

视频讲解：动态规划之子序列问题，换汤不换药 | LeetCode：1035.不相交的线_哔哩哔哩_bilibili

思考：本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

代码实现(与1143.最长公共子序列相同 )：

class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[nums1.size()][nums2.size()];}
};

时间复杂度: O(n * m)，其中 n 和 m 分别为nums1 和 nums2的长度
空间复杂度: O(n * m)

三、53. 最大子序和动态规划

题目链接/文章讲解：代码随想录

视频讲解：看起来复杂，其实是简单动态规划 | LeetCode：53.最大子序和_哔哩哔哩_bilibili

思考：

1.确定dp数组（dp table）以及下标的含义

dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]

2.确定递推公式

dp[i]只有两个方向可以推出来：

dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
nums[i]，即：从头开始计算当前连续子序列和
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
3.dp数组的初始化

dp[0] = nums[0]

4.确定遍历顺序

从前向后

5.举例推导dp数组

代码实现：

贪心：

class Solution {
public:int maxSubArray(vector<int>& nums) {int result = INT_MIN;int count = 0;for(int i = 0;i < nums.size();i++){count += nums[i];if(count > result) result = count;if(count < 0) count = 0;}return result;}
};

动态规划：

class Solution {
public:int maxSubArray(vector<int>& nums) {if (nums.size() == 0) return 0;vector<int> dp(nums.size());dp[0] = nums[0];int result = dp[0];for (int i = 1; i < nums.size(); i++) {dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值}return result;}
};