SuperGlue: Learning Feature Matching with Graph Neural Networks 论文解析

本文主要是介绍SuperGlue: Learning Feature Matching with Graph Neural Networks 论文解析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

SuperGlue: Learning Feature Matching with Graph Neural Networks 论文解析

简介

出发点

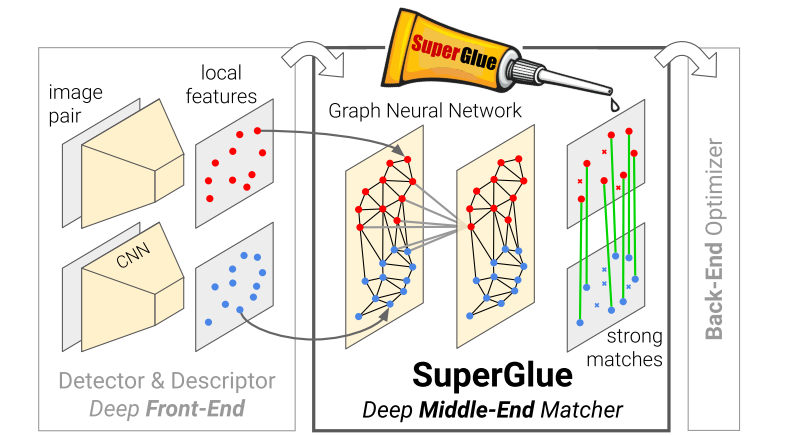
快速最临近邻搜索（FLANN）算法常常被用于匹配得到最近邻特征点，从而得到图片A和图片B中的特征点的匹配对。但是本文认为，特征点的提取与描述采用复杂的深度学习算法后不再是限制因素，而Naive的匹配方法才是限制其性能的关键点。因此本文在SuperPoint的基础上提出了一种匹配算法，取得了匹配性能的极大改进。

方法

理解本文需要有如下的基础知识：

图卷积神经网络
注意力机制
最优搬运问题

图卷积神经网络

图卷积神经网络是目前很火的内容，为了理解本文，需要有如下的相关知识，即网络的计算方式。

在这里插入图片描述

图网络分为很多层，和普通卷积网络类似
图网络每一层中有节点和边，节点和边的连接关系不规则
定义卷积操作，即下一层节点的值，为上一层节点连接的所有节点的函数。
$x_i^{n+1} = f(x_1^n,x_2^n,x_3^n,\cdots,x_m^n),x_{1\to m}为所有与i节点关联的节点$
- 例如： $x_1^2$ 为第二层第一个节点与 $x_2,x_3$ 节点相连，因此计算为：
  $x_1^2 = f(x_1^1,x_3^1,x_4^1)$
通过定义不同的卷积方法 $f$ ,得到不同类型的图卷积网络，文中借鉴注意力机制定义了卷积方法。

注意力机制

文中通过注意力机制构建了卷积计算方法，所谓的注意力机制即计算如下的权重，然后进行加权求和。
简化版本为：
$A=\alpha_1 x_1 + \alpha_2 x_2 + \cdots + \alpha_m x_m$

其中加权的权重即为注意力的权重，即下一层的信息为上一次相关节点的加权和。

如何确定加权权重呢？注意力机制提出采用查询（query）、关键值（key）以及值（value）机制。
在这里插入图片描述

首先对每一个节点计算三个值，即 $q, k, v$
$q_i = W_1 x_i + b_1 \\ k_i = W_2 x_i + b_2 \\ v_i = W_3 x_i + b_3$
对每一个节点计算 $\alpha_j,j$ 为所有连接的节点
计算加权和

最优搬运问题

首先看特征点匹配问题描述。

假设存在特征点集合 $A, B$ ，其中每一个点与另一个集合所有点的匹配概率组合成得分矩阵 $S$ 。因此得分矩阵 $S$ 定义如下：

$S_{m \times n}=\left[\begin{array}{cccc} S_{11} & \cdots & S_{m 1} \\ \vdots & \ddots &\vdots \\ S_{1 n} &\cdots & S_{m n} \end{array}\right]$
其中， $s_{i,j}$ 为 $A$ 中第 $i$ 个点与 $B$ 中第 $j$ 个点的匹配概率。
因此定义如下优化问题：

优化目标
计算分配矩阵 $P$ ，使得概率最大（得分最高）
约束条件
$A$ 中每个特征点只能匹配 $B$ 中其中一个特征点或者无匹配

等价于有 $A$ 集合中的货物，需要搬运到 $B$ 集合的洞中，一个货物只能放一个洞，一个洞只能放一个货物。

具体的算法参考

网络架构

有了前面的基础，论文中的网络结构则更为容易理解。

主要分为如下几个部分：

关键点位置编码
基于注意力机制的图卷积网络
计算得分矩阵
利用得分矩阵 + 最优搬运问题得到分配矩阵

位置编码

将视觉描述子信息和位置信息融合，但是二者维度不一样，因此中间加了一个MLP网络。
$x_i = d_i + \text{MLP}_{enc}(p_i)$
其中，MLP网络具体如下：

包括，位置信息 $x_i,y_i)$ 和当前点得分 $s_i$

注意力图卷积神经网络

L层网络，每一层包含自相关的图结构和互相关的图结构更新参数。
- Self 层：每个特征点和同一张图片中的其他特征点相连构成图结构
- Cross 层：每个特征点和另一张图片中的特征点相连构成图结构
提出这样结构的思想在于模拟人匹配特征点的过程，即看一下 $A$ 本身的结构，然后看一下 $B$ 对应的特征点，不断的来回看得到匹配结果。
每一层网络的更新公式如下

$}^{(\ell+1)} \mathbf{x}_{i}^{A}={ }^{(\ell)} \mathbf{x}_{i}^{A}+\operatorname{MLP}\left(\left[{ }^{(\ell)} \mathbf{x}_{i}^{A} \| \mathbf{m}_{\mathcal{E} \rightarrow i}\right]\right)$

其中， $}^{(\ell)} \mathbf{x}_{i}^{A}$ 为当前层数据， $∣ ∣$ 符号表示两个向量拼接， $\mathbf{m}_{\mathcal{E} \rightarrow i}$ 为注意力更新向量。

根据上面对注意力的解释，其计算方式为：

$\mathbf{m}_{\mathcal{E} \rightarrow i}=\sum_{j:(i, j) \in \mathcal{E}} \alpha_{i j} \mathbf{v}_{j}$

$\begin{aligned} \mathbf{q}_{i} &=\mathbf{W}_{1}^{(\ell)} \mathbf{x}_{i}^{Q}+\mathbf{b}_{1} \\ \left[\begin{array}{c} \mathbf{k}_{j} \\ \mathbf{v}_{j} \end{array}\right] &=\left[\begin{array}{l} \mathbf{W}_{2} \\ \mathbf{W}_{3} \end{array}\right](\ell) \mathbf{x}_{i}^{S}+\left[\begin{array}{l} \mathbf{b}_{2} \\ \mathbf{b}_{3} \end{array}\right] \end{aligned}$