数据结构与算法基础（王卓）（28）线性表的查找（2）：顺序查找（二分查找、分块查找)

目录

二、折半查找（二分或对分查找)

Project 1：

修正后的结果如下：

Project 2：

问题（1）：【ST.R[mid].key】

问题（2）：等于：（==）而非（=）

问题（3）：关于除、除以、整除

一、关于除和除以的区别：

二、关于整除的问题：

问题（4）：low等于high时我们应该怎么处理？

所以对于这个情况，我们还是把他放到while循环里面比较合适

Project 3：（最终结果）

PPT上写的标准答案版本（确实也有可取之处）

PPT上补充：递归实现版本

三、分块查找

---

二、折半查找（二分或对分查找)

前置条件和前面一样

最开始根据PPT示(实)例写出的程序框架：

一开始：

low：第一位

high：最后一位

mid：正中间

查找数小于mid：

把high移动到mid前面一位（ - 1）

再取新mid = 新【正中间】

查找数大于mid：

把low移动到mid后面一位（ + 1）

再取新mid = 新【正中间】

然而这里，我写的只是一些框架的核心规则，并没有梳理出程序具体是怎么运行的逻辑流程

所以写的和标准答案写的不一样：

Project 1：

int Seaarch_Bin(SSTable ST, KeyType key)
//binary：二进制的; 仅基于两个数字的; 二元的; 由两部分组成的;
{int low = 1, high = ST.length, mid = (low + high) / 2;while (key != mid){if (key < mid){high = mid - 1;mid = (low + high) / 2;}else if (key < mid)//else{low = mid + 1;mid = (low + high) / 2;}}if (low > high)return false;elsereturn mid;
}

里面除了梳理逻辑以外，还存在另外的诸多问题，当然：

写程序之前最好肯定还是梳理出程序具体是怎么运行的逻辑流程，这是肯定的

上面这一版本还存在着诸多的问题：

• key在比较时不应该写【mid】应改成【ST.R[mid].key】（Project 2中我们会对此作出具体详细的剖析解释）
• while循环当中无论是在哪种情况（分支），（都）始终执行【mid = (low + high) / 2;】语句，应当（可以）考虑合并语句在【if】语句之外

修正后的结果如下：

（我觉得修改成如下结果以后，这个结果写的也没有错，只不过我没有那么确定一定没错）

int Seaarch_Bin(SSTable ST, KeyType key)
//binary：二进制的; 仅基于两个数字的; 二元的; 由两部分组成的;
{int low = 1, high = ST.length, mid = (low + high) / 2;while (key != ST.R[mid].key){if (key < ST.R[mid].key)high = mid - 1;else if (key < ST.R[mid].key)//elselow = mid + 1;mid = (low + high) / 2;}if (low > high)return false;elsereturn mid;
}

---

除此之外，我们首当其冲要做的：就是要梳理出程序具体是怎么运行的逻辑流程

把程序转换为和PPT上类似的逻辑形式：（但是这并不代表我写的是错的）

Project 2：

int Seaarch_Bin(SSTable ST, KeyType key)
//binary：二进制的; 仅基于两个数字的; 二元的; 由两部分组成的;
{//不是从R开始吗？？？int low = 1, high = ST.length, mid = (low + high) / 2;while (low<=high)//一开始我们是想写(key != mid)的判断语句的，但是如果这样写的话我们最后就无法判断他有没有找到{if (key = mid)return mid;else if (key < mid){high = mid - 1;mid= (low + high) / 2;}else if (key > mid)//else{low = mid + 1;mid = (low + high) / 2;}}return 0;
}

问题（1）：【ST.R[mid].key】

key在比较时不应该写【mid】应改成【ST.R[mid].key】

（Project 1中也有类似一样的问题）

具体解释：

---

首先，我们要意识到：

我们的key要对比的对象，是顺序表ST（数组）内部的具体某个位序（某一格）里面的具体数值

 这个时候我们再去看顺序表的构造，我们就会意识到：

事实上实际顺序表ST和我们原来想当然的写的程序的东西不一样

typedef int KeyType;

//数据元素类型定义

struct ElemType

{

    KeyType key;  //关键字域

    //...           //其他域

};

struct SSTable

    //Sequential Search Table

{

    ElemType* R;  //表基址

    int length;   //表长

}; 

SSTable ST;  //定义顺序表ST

实际上，我们前面写程序的效果是：

让【key】和【指针指向的元素位序序号】去比较

而我们实际需要实现的效果是：

让【key】和【指针指向的元素数据】去比较

而这个KeyType元素数据（关键字数据），则在：

表基址R（虽然我也不知道这个表基址是什么玩意）的关键字域key当中

加上数据类型：

在【（ElemType*）类型的】表基址R的【（KeyType）类型的】关键字域key当中

所以，mid应改为：ST.R[mid].key

---

而这样的解释，实际上也顺带解决了我们在编写程序时：

数组地址顺序不是从R开始吗？？？

的问题

---

问题（2）：等于：（==）而非（=）

---

问题（3）：关于除、除以、整除

一、关于除和除以的区别：

6除以2：divided by

6÷2＝3

6除2：divide

2÷6＝⅓

2除6：divide

6÷2＝3

2除以6：divided by

2÷6＝⅓

二、关于整除的问题：

整除的取整：

取整数，舍去小数

注意：并非四舍五入

在计算机当中，关于除法，只有一个运算符号，那就是“/”

而关于其是否整除：

是表示整除的取整结果【注意：并非四舍五入】还是带小数的最终运算结果，取决于除数和被除数，更准确的说，是除法过程中，所有的运算量

若所有的运算量【所有的 除数和被除数】都为整型（int型）：

结果取整，舍去小数（注意：不是四舍五入）

若所有的运算量【所有的 除数和被除数】中只要有一个运算量为实型（实数类型：float、double）

结果保留小数（保留小数位数格式向实数的类型看齐，能更精确就更精确）

---

问题（4）：low等于high时我们应该怎么处理？

在前面的实例中，我们写了low和high大于和小于的情况

那么当low和high等于时我们应该怎么处理？

设计具体实例尝试，假设：

位序	1	2	3
数据	22	23	24
指针	low	mid	high

 所以我们最终得到的结论就是说：

当low等于high时：

如果key不等于【low和high还有mid】，那么就查找失败

如果等于，输出指针

所以对于这个情况，我们还是把他放到while循环里面比较合适

---

Project 3：（最终结果）

int Seaarch_Bin(SSTable ST, KeyType key)
//binary：二进制的; 仅基于两个数字的; 二元的; 由两部分组成的;
{int low = 1, high = ST.length, mid = (low + high) / 2;while (low <= high){if (key == ST.R[mid].key)return mid;else if (key < ST.R[mid].key)high = mid - 1;else if (key > ST.R[mid].key)//elselow = mid + 1;mid = (low + high) / 2;}return 0;
}

附：

PPT上写的标准答案版本（确实也有可取之处）

他相当于在我们前面写的程序的基础上再简化一步：

一开始不必给mid赋值，只需要在每次循环的开始给mid进行赋值操作即可

int Seaarch_Bin(SSTable ST, KeyType key)
//binary：二进制的; 仅基于两个数字的; 二元的; 由两部分组成的;
{int low = 1, high = ST.length,mid; while (low <= high){mid = (low + high) / 2;if (key == mid)return mid;else if (key < ST.R[mid].key)high = mid - 1;else//else if (key > ST.R[mid].key)low = mid + 1;   }return 0;
}

PPT上补充：递归实现版本

int Search_bin(SSTable& S, KeyType e, int low, int high)
{if (low > high)return -1;int mid = (high + low) / 2;if (e == S.R[mid].key)return mid;if (e < S.R[mid].key)return Search_bin(S, e, low, mid - 1);elsereturn Search_bin(S, e, mid + 1, high);
}

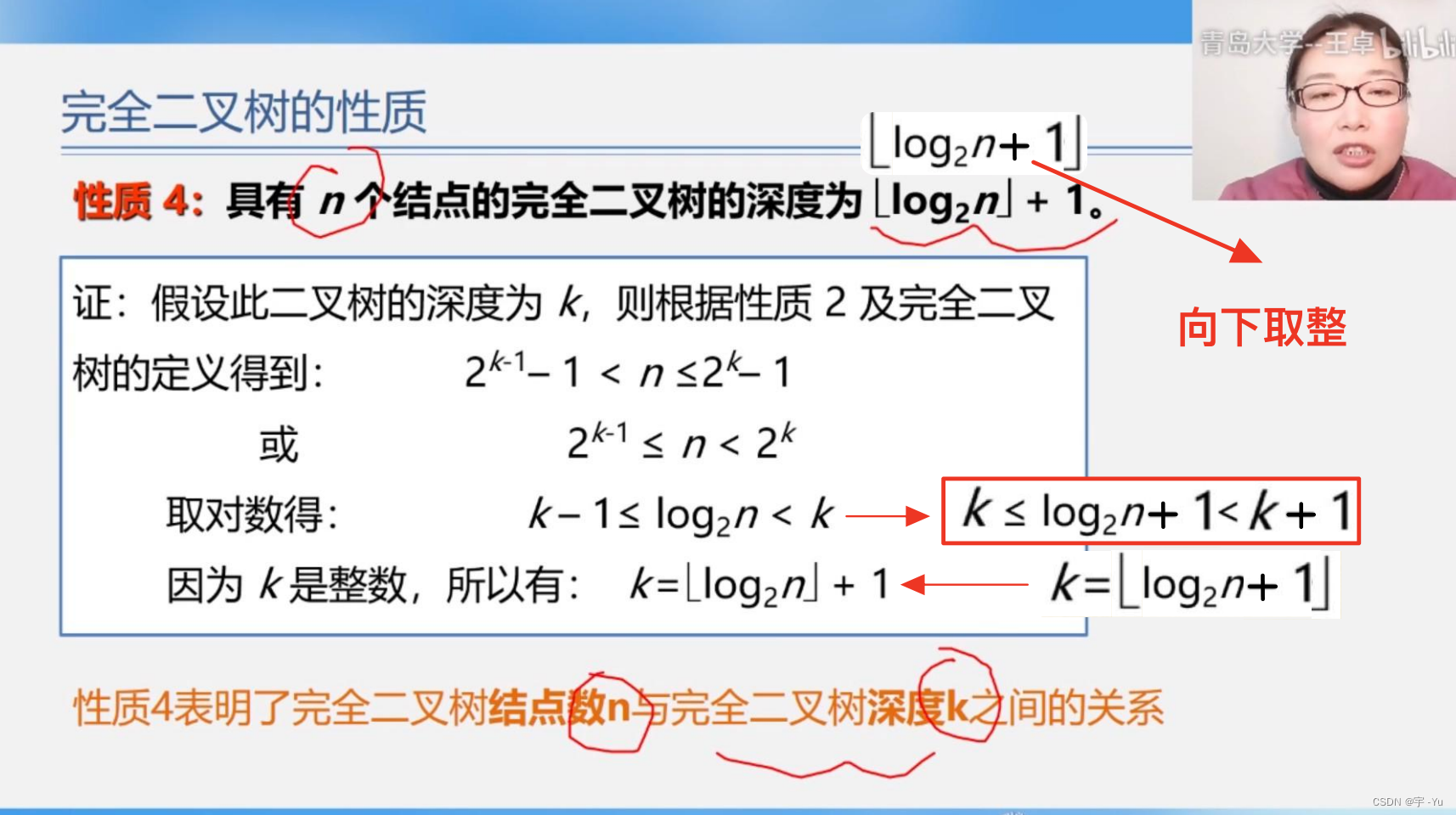
 平均查找长度推导参考：第五章《树和二叉树》P34

三、分块查找

---

不考察代码

不过分块查找的代码怎么实现以后有时间倒也可以研究一下，还是挺有意思的