Two Buildings（决策单调性+分治）

本文主要是介绍Two Buildings（决策单调性+分治），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

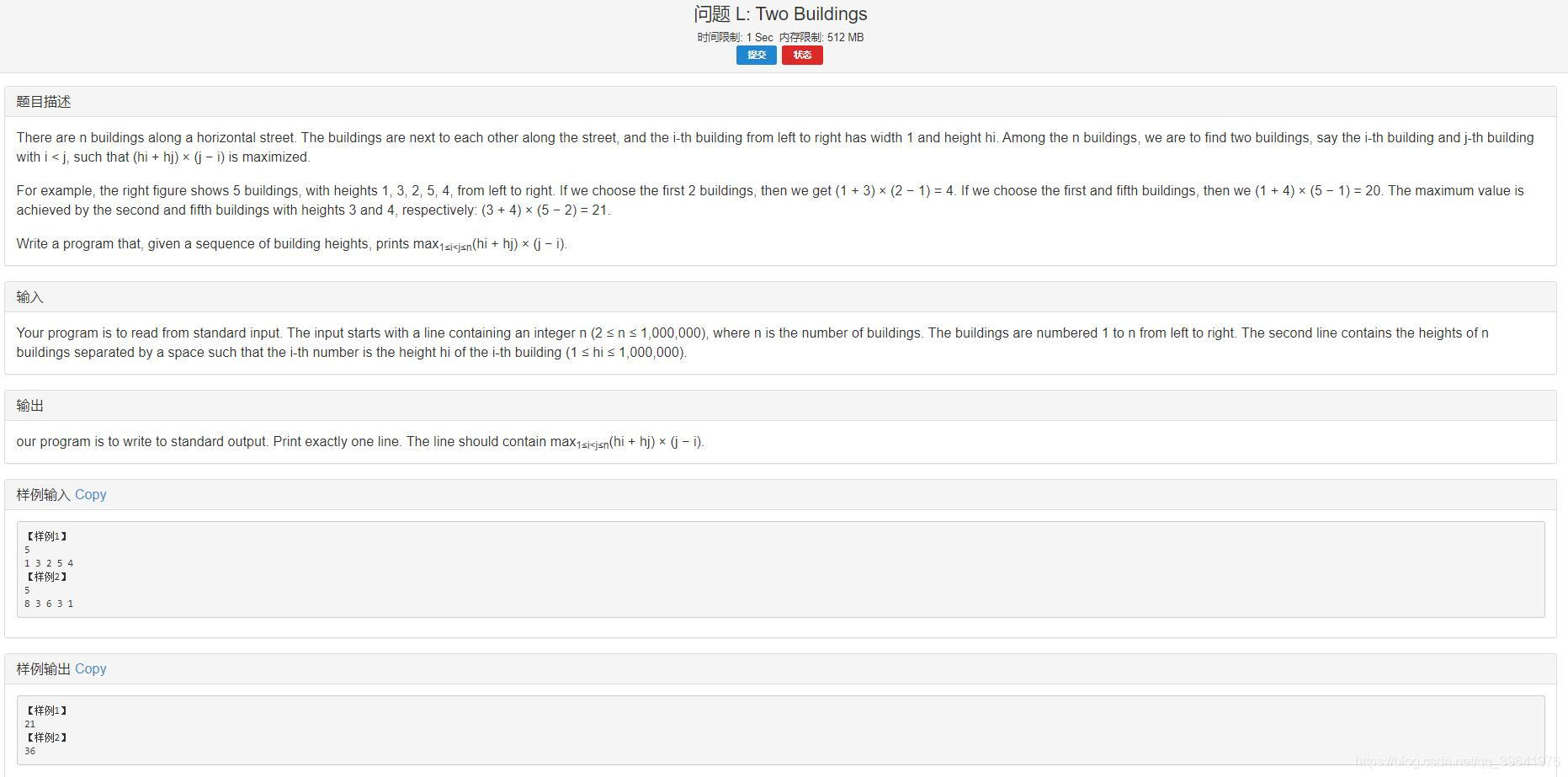
在这里插入图片描述
题目大意：
给定一个长度为 $n$ 的数组 $h$ 求：
$max(\ (h_i+h_j)(j-i)\ )$
题目分析：
此题可转化为求：
$max(\ (h_j-(-h_i))(j-i)\ )$
这个就相当于在二维坐标系中求最大矩形的面积，我们设 $a, b$ 数组分别为矩形的左下角和右上角那两个坐标的纵坐标（其横坐标就是其数组下标），则题目所求即为：
$max(\ (b_j-a_i)(j-i)\ )$
将上式和题目所求联立可得 $a_i=-h_i,b_i=h_i$ ，这样我们就可以得到 $a, b$ 数组了
我们继续考虑如何求 $max(\ (b_j-a_i)(j-i)\ )$ ：
我们发现对于一个给定 $a_i$ 在选择 $b_j$ 与之配对时 $b_j$ 是有决策单调性的：越往右上越优，即对于下面两个决策：
$b_i\le b_j(i<j)$
决策 $b_j$ 显然优于决策 $b_i$ 所以可以直接将 $b_i$ 状态删掉，对 $a$ 数组同理（如果不理解在纸上画一画图可能就明白了）
接下来我们考虑如何快速处理出答案：
设 $a, b$ 数组分别有 $n, m$ 个元素（已按从左下到右上排好序）， $a . x$ 表示原数组下标即二维平面的横坐标， $a . y$ 表示二维平面的那个纵坐标， $b$ 数组同理
用 $s o l v e (l 1, r 1, l 2, r 2)$ 表示 $a$ 数组下标从 $l 1$ 到 $r 1$ ， $b$ 数组从 $l 2$ 到 $r 2$ 的最优解，我们采用一下过程进行分治：
取 $mid=\frac{l1+r1}2$ 我们扫描 $b$ 数组并记录对 $a_{mid}$ 的最优解的下标 $p o s$ ，然后答案就是 $a_{mid},b_{pos}$ 构成的矩形， $s o l v e (l 1, m i d - 1, l 2, p o s)$ ， $s o v l e (m i d + 1, r 1, p o s, r 2)$ 三者的最大值（因为决策是具有单调性的）

具体细节见代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<set>
#include<map>
#include<stack>
#define ll long long
#define inf 0x3f3f3f3f
#define Inf 0x3f3f3f3f3f3f3f3f
using namespace std;
ll read()
{ll res = 0,flag = 1;char ch = getchar();while(ch<'0' || ch>'9'){if(ch == '-') flag = -1;ch = getchar();}while(ch>='0' && ch<='9'){res = (res<<3)+(res<<1)+(ch^48);//res*10+ch-'0';ch = getchar();}return res*flag;
}
const int maxn = 5e6+5;
const int mod = 1e9+7;
const double pi = acos(-1);
const double eps = 1e-8;
struct node{ll x,y;bool operator < (const node b) const {if(x == b.x) return y < b.y;return x < b.x;}
}a[maxn],b[maxn];
ll n,m,h[maxn];
bool vis[maxn];
void init_a()
{memset(vis,0,sizeof(vis));sort(a+1,a+n+1);int last = 1,cnt = 0;for(int i = 2;i <= n;i++)if(a[i].y >= a[last].y) vis[i] = true;else last = i;for(int i = 1;i <= n;i++)if(!vis[i]) a[++cnt] = a[i];n = cnt;
}
void init_b()
{memset(vis,0,sizeof(vis));sort(b+1,b+m+1);int last = m,cnt = 0;for(int i = m-1;i;i--)if(b[i].y <= b[last].y) vis[i] = true;else last = i;for(int i = 1;i <= m;i++)if(!vis[i]) b[++cnt] = b[i];m = cnt;
}
ll calc(ll i,ll j)
{if(a[i].x>b[j].x && a[i].y > b[j].y)return -Inf;return (b[j].x-a[i].x)*(b[j].y-a[i].y);
}
ll solve(ll l1,ll r1,ll l2,ll r2)
{if(l1>r1 || l2>r2) return 0;int mid = l1+r1>>1;int pos = l2;for(int i = l2+1;i <= r2;i++)if(calc(mid,pos) < calc(mid,i))pos = i;return max({calc(mid,pos),solve(l1,mid-1,l2,pos),solve(mid+1,r1,pos,r2)});
}
int main()
{n = read();m = n;for(int i = 1;i <= n;i++){h[i] = read();a[i].x = b[i].x = i;a[i].y = -h[i];b[i].y = h[i];}init_a();init_b();printf("%lld\n",solve(1,n,1,m));return 0;
}