本文主要是介绍机器学习模型中的因果关系:引入单调约束,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
单调约束是使机器学习模型可行的关键,但它们仍未被广泛使用欢迎来到雲闪世界。

碳ausality 正在迅速成为每个数据科学家工具包中必不可少的组成部分。
这是有充分理由的。
事实上,因果模型在商业中具有很高的价值,因为它们为“假设”情景提供了更可靠的估计,特别是在用于做出影响业务结果的决策时。
在本文中,我将展示如何通过简单的更改(实际上添加一行代码)将传统的 ML 模型(如随机森林、LightGBM、CatBoost 等)转变为回答因果问题的可靠工具。
因果 ML 模型与传统 ML 模型
假设我们在一家房地产公司工作,公司的业务是购买房屋,然后以更高的价格转售。
我们收集了过去交易过的房屋数据。数据集包含 3 个变量:
- “平方英尺”,房屋的平方英尺数;
- “整体状况”,对房产整体状况的数字评分,评分范围为 1 至 9(分数越高越好);
- “房屋售价”,即房屋最终售出的价格。
以下是数据集中的前 5 栋房屋:
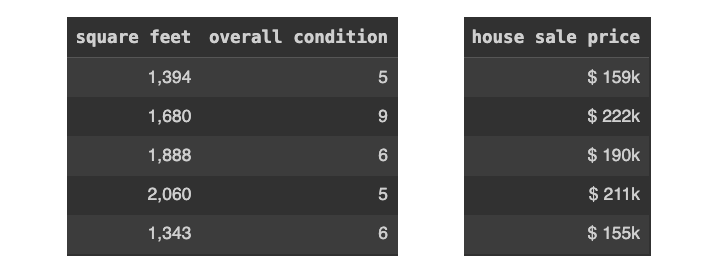
[作者图片]
与以相同方式处理所有特征的传统 ML 模型相比,因果 ML 模型区分了两种类型的特征:
- 协变量特征,仅可观察到的特征;
- 处理特征,这些特征可能会受到决策者(在本例中为我们的公司)的影响。
在我们的案例中,我们当然无法改变房屋的面积。我们能做的是通过装修改善房产状况,希望这会影响目标变量(即我们能够以更高的价格出售房屋)。
因此“平方英尺”是一个协变量特征,“整体状况”是一个治疗特征。
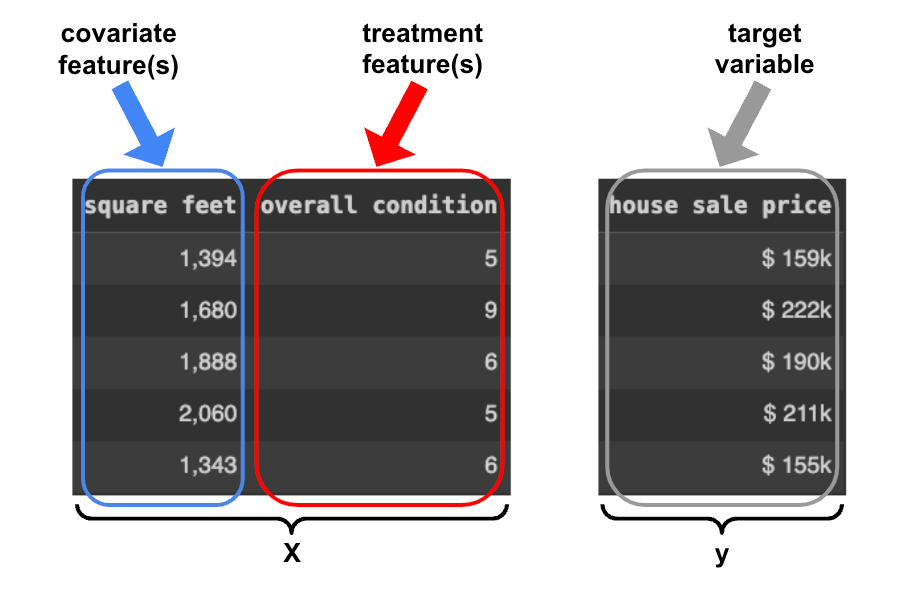
[作者图片]
因果模型的主要优势是能够回答因果(或“假设”)问题。
例如,假设我们公司刚刚购买了一栋新房,建筑面积为 3,000 平方英尺,当前状况评级为 5。该公司有两种选择:
- 按原样出售房屋;
- 花费 30,000 美元翻新房屋,将状况评级从 5 提高到 7,然后出售。
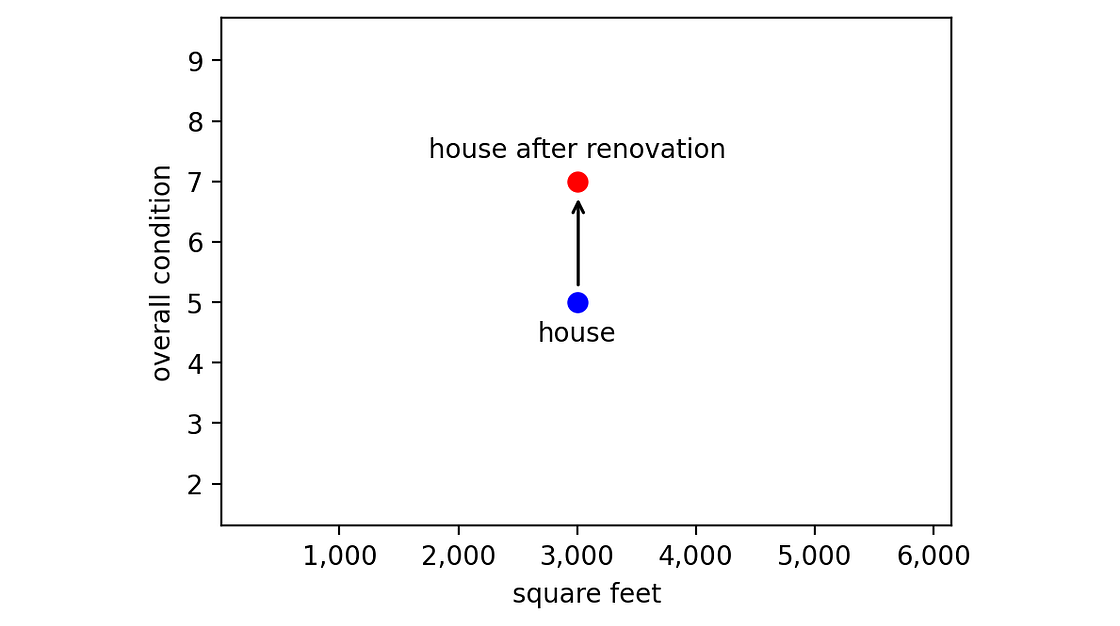
[作者图片]
公司应该做什么?
“我们应该装修这所房子吗?”
我们是数据科学家,所以我们首先想到的就是训练一个机器学习模型来预测房屋在装修前后的最终价格。
假设我们决定为此目的使用决策树。我们首先在训练数据集上拟合模型:
从sklearn.tree导入DecisionTreeRegressor decision_tree = DecisionTreeRegressor( max_depth= 3 , min_samples_leaf= 10) decision_tree.fit(X_train, y_train)然后,我们使用该模型预测两种情况下(有或无装修)的销售价格。
X = [ [3_000, 5],3_000 , 5 ], [ 3_000 , 7 ]
]决策树.预测(X)以下是结果:
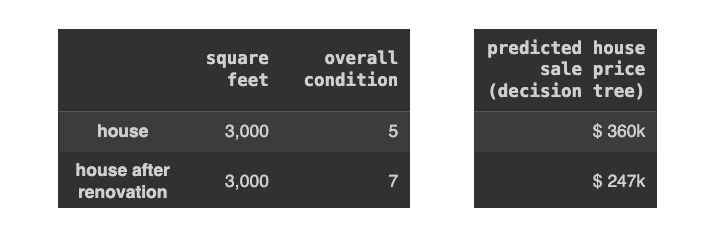
[作者图片]
我希望你不要与销售部门分享这些结果——他们可能会禁止你再次说“机器学习”。
他们说得对。这个结果显然是荒谬的。通过翻修改善房屋状况怎么会降低其价值,使其从 36 万美元降至 24.7 万美元呢?
我们的模型肯定有问题。
由于该模型仅基于两个特征,我们可以在二维热图中直观地看到预测阈值:
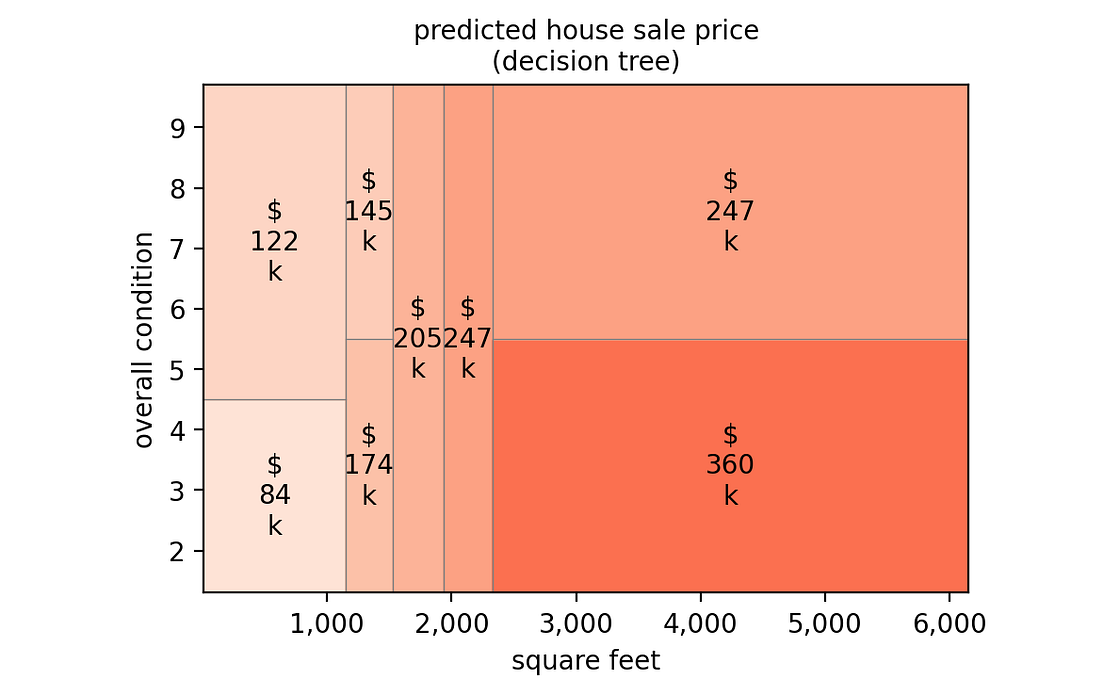
[作者图片]
这个模型中有几件事完全没有意义:
- 对于面积在 1,150 到 1,500 平方英尺之间的房屋,将其状况从 5 或更低改善到 6 或更高,会使其价值从 174,000 美元降低到 145,000 美元。
- 同样,对于面积超过 2,300 平方英尺的房屋,将其状况从 5 或更低改善到 6 或更高,会使其价值从 36 万美元降低到 24.7 万美元。
我们不能相信这些预测。我们确信房屋装修后的价值不可能低于装修前的价值,所以我们需要一种方法将这一常识“转移”到我们的模型中。
引入单调约束
我们的 ML 模型的一个理想特性是,在我们改善房屋状况后,模型应该预测一个大于或等于原始值的值。相反,如果房屋状况更糟,则该值应该更小或相等。
因此,让我们以数据点(面积为 3,000 平方英尺且状况评级为 5 的房屋)为例,并可视化我们希望模型捕捉到的这个属性。
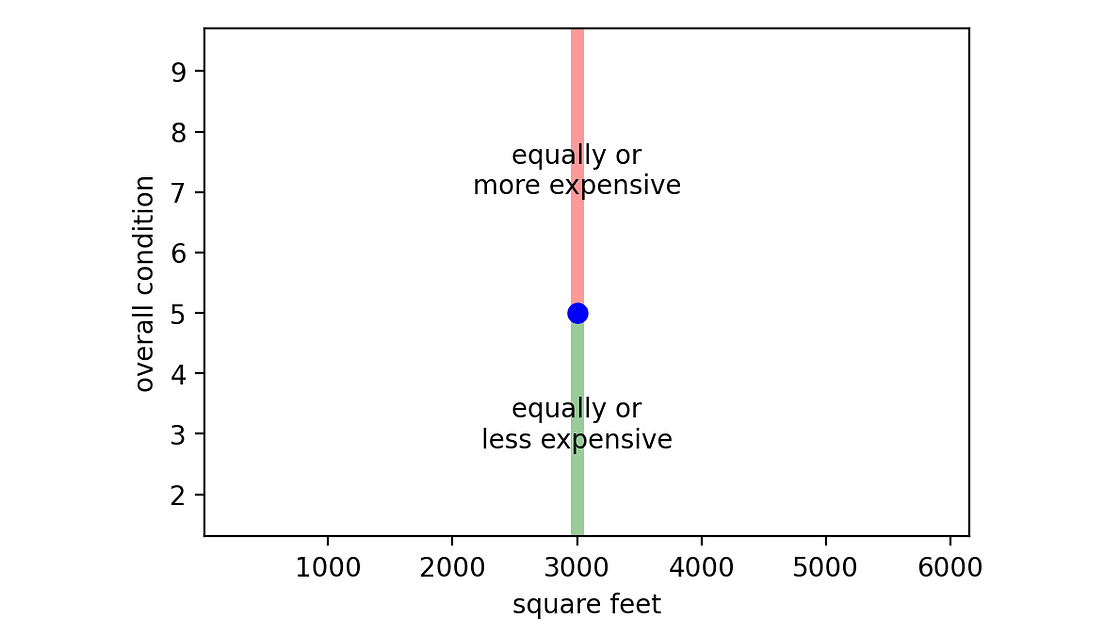
[作者图片]
这被称为“单调约束”,因为它没有说明关系的类型(线性、二次……),而只说明了关系的方向(非减少与非增加)。
这个要求比线性约束(即线性回归施加的约束)弱得多,这是很好的,因为:
自然界中很少有关系是线性的,但自然界中的许多关系都是单调的。
这就是为什么线性回归通常表现不佳的原因:它对模型施加了线性约束,这在大多数实际情况下是一个不切实际的强假设。
薪水会随着经验的增加而增加吗?会,但只是单调增加,而不是线性增加。冰淇淋销量会随着温度的升高而增加吗?会,但只是单调增加,而不是线性增加。你懂的。
对于每个特征,我们可以想象以下三种情况之一:
- +1:当特征增加时,预测必须大于或等于;
- 0:没有单调约束(默认);
- -1:当特征增加时,预测必须更小或相等。
基于我们所说的,我们需要在称为“整体状况”的特征上添加“+1”单调约束,以确保更好的分数始终对应于更高或相同的价格。
但是“平方英尺”又如何呢?
从视觉上看,这是仅对特征“整体条件”应用单调约束与将其应用于两个特征之间的区别:
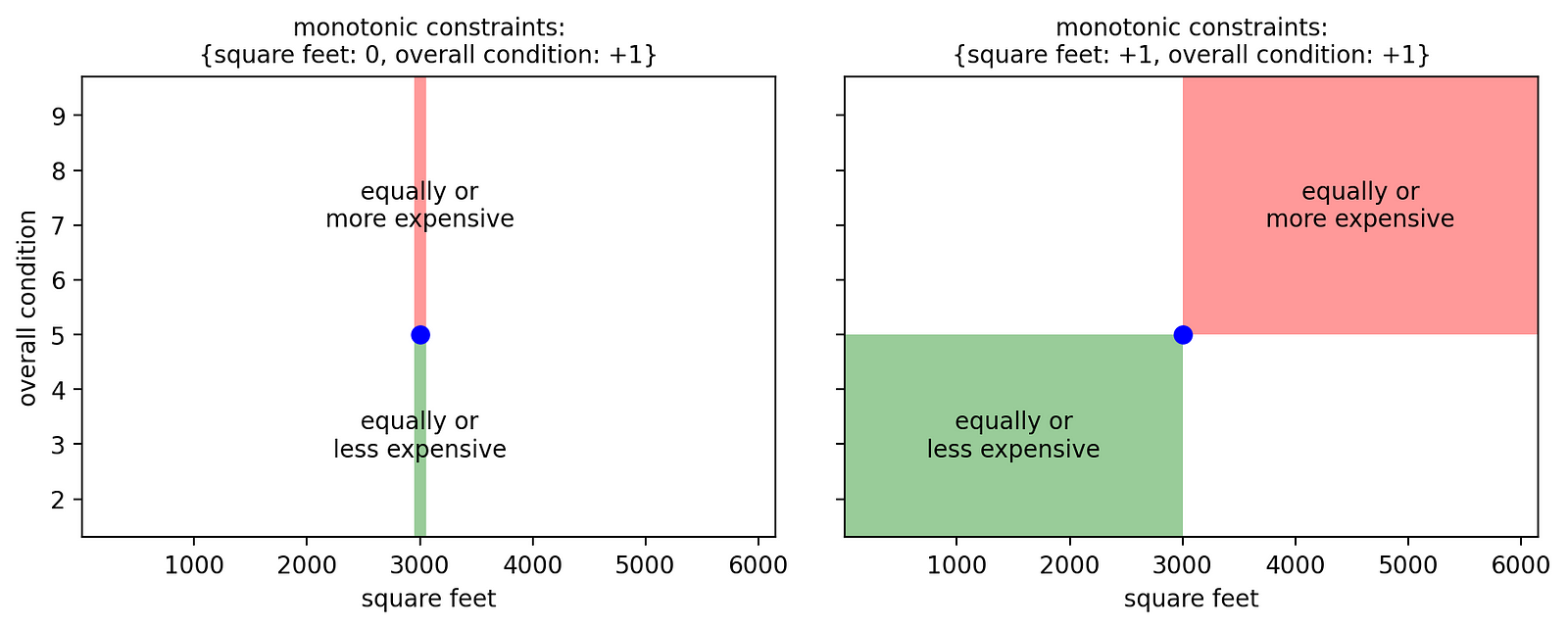
[作者图片]
让我们看看左边的图。如果我们只对“整体状况”应用单调约束,我们就无法对面积不同的房屋做出任何判断。在这种情况下,我们会得到:
- (平方英尺:3,000,整体状况:5)-> 价格:x;
- (平方英尺:3,000,整体状况:7)-> 价格:y ≥ x;
- (平方英尺:4,000,整体状况:7) -> 价格:z,可能高于或低于x和y,因为对变量“平方英尺”没有限制。
相反,在右侧的图中,我们对两个特征都应用了正约束,因此:
- (平方英尺:3,000,整体状况:5)-> 价格:x;
- (平方英尺:3,000,整体状况:7)-> 价格:y ≥ x;
- (平方英尺:4,000,整体状况:7)-> 价格:z ≥ y ≥ x。
我认为第二种情况更符合我们的直觉。
请注意,在这些图中,我们观察了单调约束对坐标为 (3,000, 5) 的单个数据点的影响,但相同的推理也适用于数据集内的任何数据点。
让我们看看将这些单调约束应用到我们的预测模型后会发生什么。
在 Python 中强制执行单调约束
好消息是,单调约束得到了最流行的 Python ML 库(如 Scikit-learn、LightGBM 和 CatBoost)的支持,只需添加一行代码即可应用。
就我们的决策树而言:
decision_tree_with_constraints = DecisionTreeRegressor(max_depth=3, 3, min_samples_leaf=10,monotonic_cst=[1,1] # this line of code adds monotonic constraints
)decision_tree_with_constraints.fit(X_train, y_train)我们现在可以将非约束模型(左图)的预测热图与约束模型(右图)的预测热图进行比较。
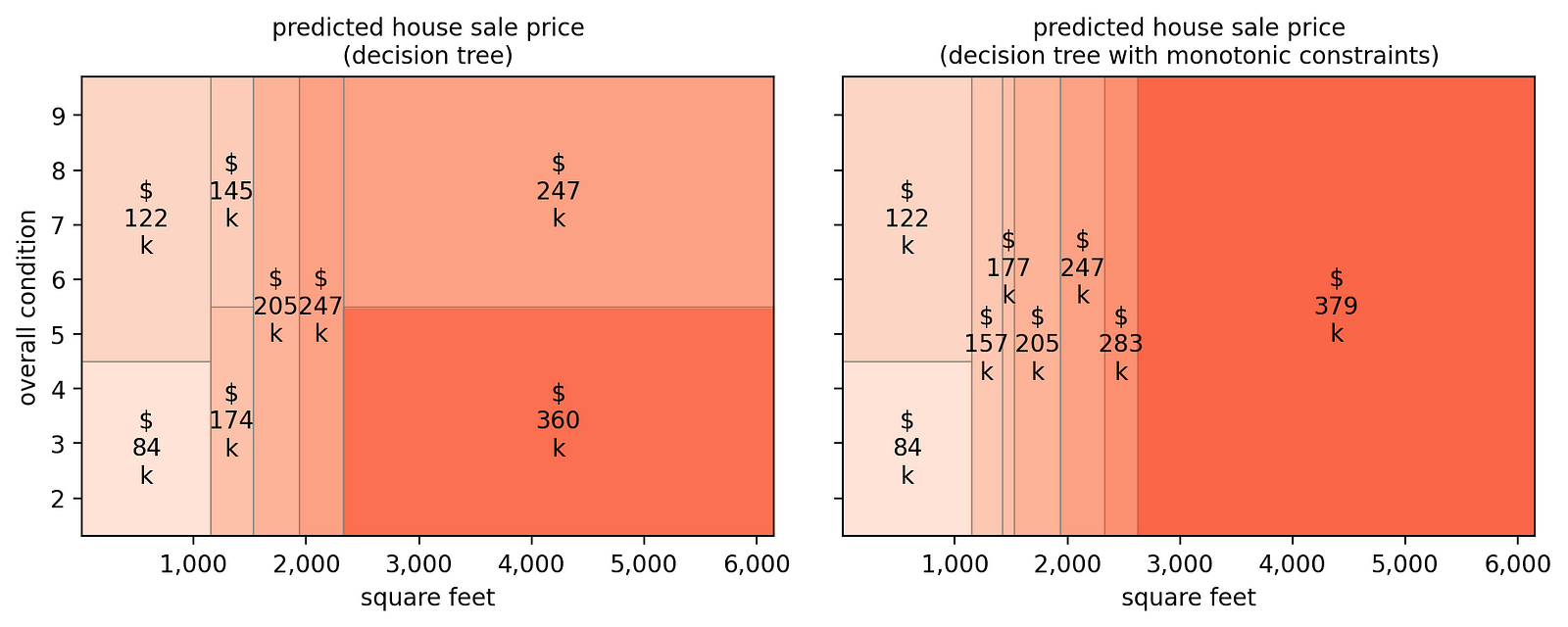
[作者图片]
新的预测(右侧图表)更有意义。事实上,它们对于“平方英尺”和“总体状况”而言都是非减少的。
但决策树可能过于简单。所以,现在让我们尝试使用性能更高的模型,例如 CatBoost。
catboost = CatBoostRegressor(silent=TrueTrue
)catboost_with_constraints = CatBoostRegressor(silent=True, monotone_constraints={"square feet": 1, "overall condition": 1}我们可以使用 CatBoost 来模拟假设情景。例如:如果我们改变面积分别为 500、1,000、2,000 或 3,000 平方英尺的房屋的“整体状况”,会发生什么?
这也被称为敏感性分析,因为它根据输入变量(房屋的整体状况)的变化来测量结果(我们的模型预测的销售价格)的敏感性。
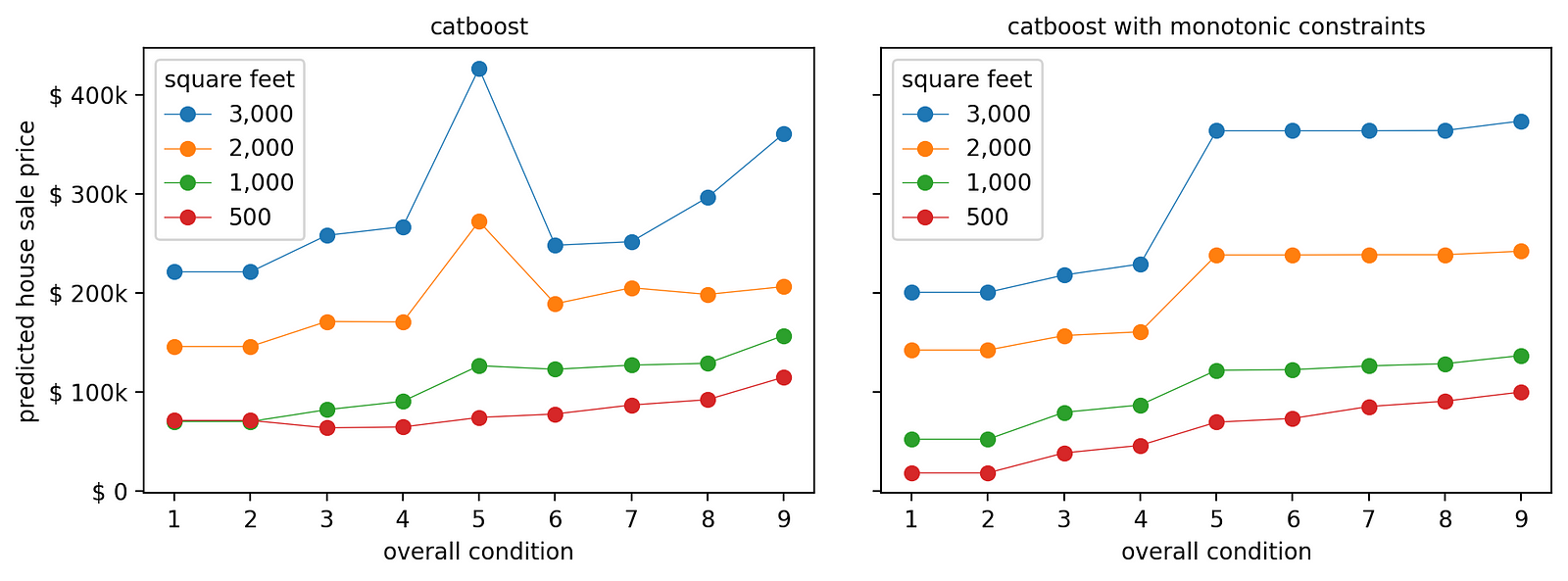
[作者图片]
受约束的版本比不受约束的版本好得多。
事实上,在约束模型中,面积较小的房屋(500 至 1,000 平方英尺)的预测价格会平稳上升。与此同时,面积较大的房屋(2,000 至 3,000 平方英尺)的状况评分提高会导致价格大幅上涨。
这给出了一个非常直接的商业见解:如果一栋房子面积很大,但状况很差(评分为 4 分或更低),那么对其进行翻新以高得多的价格出售是合理的。但是,将房屋状况改善到 5 分以上是没有意义的,因为这不会带来实质性的额外价值。
受约束模型的预测比不受约束模型的预测更容易解释。但它们的表现如何呢?例如 R 平方?
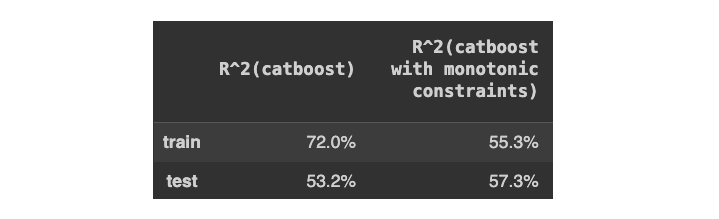
[作者图片]
不仅约束模型的样本外性能要好得多(57% 对 53%),而且约束模型的 R 平方也明显低于无约束模型的 R 平方(55% 对 72%)。
这意味着,与不受约束的模型相比,具有单调约束的模型过度拟合的程度要小得多。
这很有道理:通过施加单调约束,我们将一些关于世界的知识“转移”到模型中。这基本上就像是免费数据!
结论
在本文中,我们已经看到,向 ML 模型添加单调约束可能是一个好主意,原因如下:
- 提高回答影响商业决策的“假设”问题的可靠性;
- 在您选择的指标(例如 R 平方)方面表现更佳;
- 更少的过度拟合,因为我们直接将我们对世界的一些知识(或常识)转移到模型中。
换句话说,单调约束似乎是两个相反极端之间的最佳点:允许模型完全自由(传统的“让数据说话”方法)与强加不切实际的强烈假设(例如线性回归)。
感谢关注雲闪世界。(Aws解决方案架构师vs开发人员&GCP解决方案架构师vs开发人员)
这篇关于机器学习模型中的因果关系:引入单调约束的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







