题目传送门： http://acm.hdu.edu.cn/game/entry/problem/show.php?chapterid=1&sectionid=2&problemid=13 本题的数组实际上就是用来练习输入输出的，直接使用scanf读取即可。 #include<stdio.h>using namespace std;//HDU Buildings 水题，注意输出即可，可以处

题意：在一个n*m的矩形中，要放置很多小矩形，每个矩形必须与大矩形的边界相接触，其中有一块1*1的必须空着，他的坐标是x,y。现在问放置的小矩形面积最大值最少是多少？ 分析：因为每个小矩形要和边界互相接触，所以每个小矩形都是形如1*a这样的矩形，这样才能保证面积最小，在没有空着的矩形的情况下，最小的矩形面积肯定是1*(n+1)/2， n < m；但是若放置了一个空的1*1的矩形，那么受影

题目连接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3993 题目大意：        最初的防御战是以（0,0）为圆形R为半径的一个圆O1，问你当防御战缩小为最初的圆O1内的一个半径为r的小圆（小圆的圆心随意位置）时，各点的能在小圆内的概率最大的是哪个。 题目思路：       AC代码： #inc

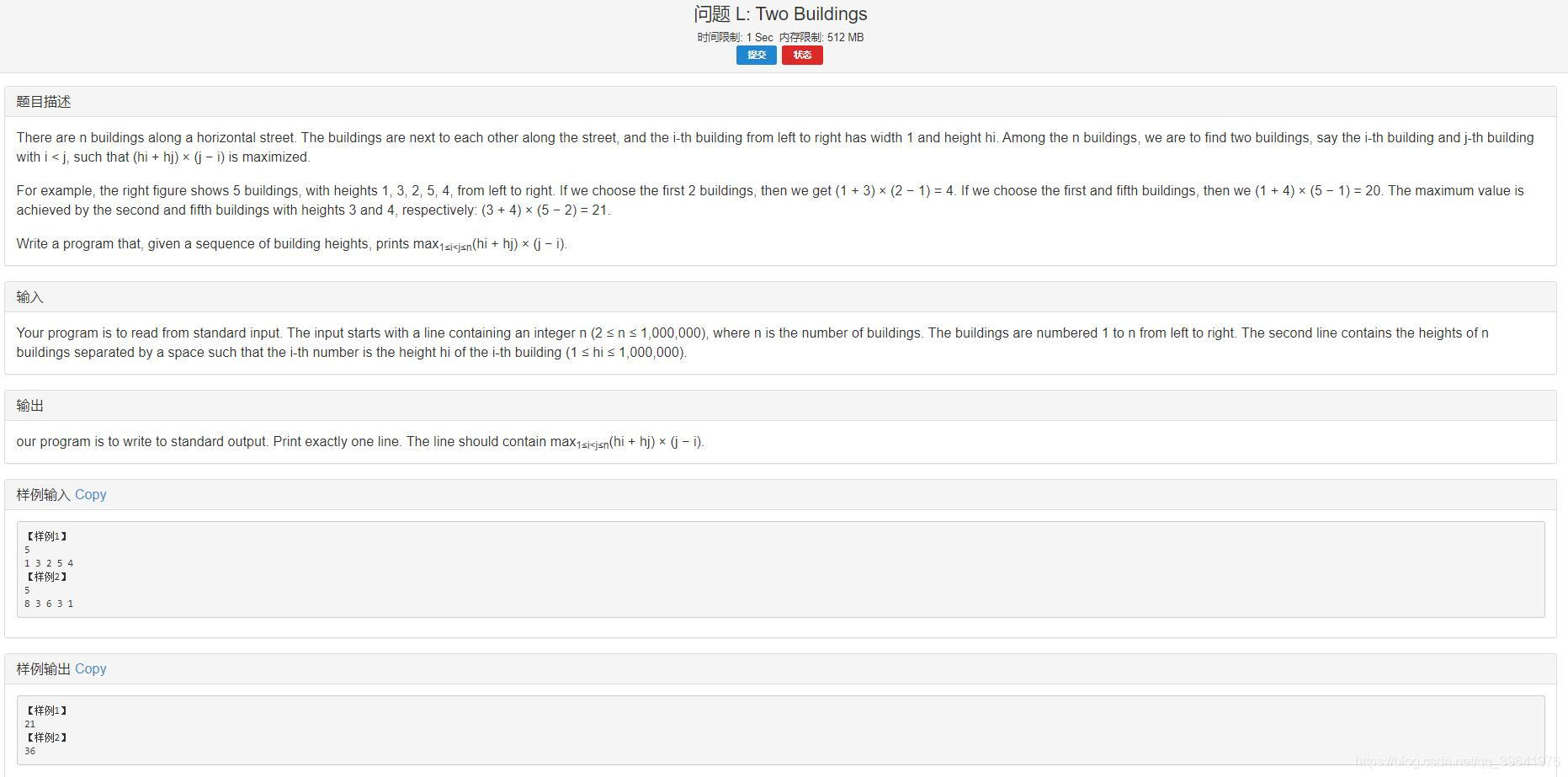
题目大意： 给定一个长度为 n n n 的数组 h h h 求： m a x ( ( h i + h j ) ( j − i ) ) max(\ (h_i+h_j)(j-i)\ ) max( (hi​+hj​)(j−i) ) 题目分析： 此题可转化为求： m a x ( ( h j − ( − h i ) ) ( j − i ) ) max(\ (h_j-(-h_i))(j-i)\ )