learnopengl——Diffuse irradiance

英文版：https://learnopengl.com/PBR/IBL/Diffuse-irradiance
中文版：https://learnopengl-cn.github.io/07%20PBR/03%20IBL/01%20Diffuse%20irradiance/

本节主要是将环境光考虑进去，进行物理渲染。

IBL or image based lighting is a collection of techniques to light objects, not by direct analytical lights as in the previous tutorial, but by treating the surrounding environment as one big light source. 基于图片的光照，是将周围的环境想象成一个巨大的光源。而巨大的光源怎么实现呢？就是借助立方体贴图了。
this is generally accomplished by manipulating a cubemap environment map (taken from a real world or generated from a 3d scene) such that we can directly use it in our lighting equations: treating each cubemap pixel as a light emitter. this way we can effectively capture an enviroment’s global lighting and general feel, giving objects a better sense of belonging in their environment.
这样将立方体贴图上的每个像素看作为一个灯光发射器。这样我们就可以运用之前的光照知识了，可以抓住全场景的光照效果，使得看起物体是属于整个环境的，因为它考虑了环境光之后的效果。

as image based lighting algorithms capture the lighting of some (global) environment its input is considered a more precise form of ambient lighting, even a crude approximation of global illumination. this makes IBL interesting for PBR as obejcts look significantly more physically accurate when we take the environment’s lighting into account.

to start introducing IBL into our PBR system let us again take a quick look at the refletance equation:

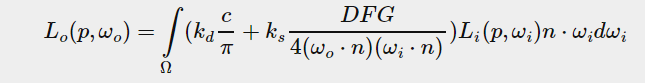
as described before, our main goal is to solve the integral of all incoming light directions wi over the hemisphere Ω. solving the intergra in the previous tutorial was easy as we knew beforehand the exact few light directions wi that contributed to the intergral.
this time however, every incoming light direction wi from the surrounding environment could potentially have some radiance making it less trivial to solve the intergral. this gives us two main requirements for solving the integral:
上面的这段话的意思是：
上一节的内容，我们只考虑四个点的光源，所以对于一点p来说，只有四个入射光方向wi对其中最后产生辐射率影响。而本节，是考虑了整个的环境光，所以不太好累加所有的方向，求积分困难。
所以针对这个情况，需要解决两个基本的问题：一个是如何采样任意方向的辐射率‘；二个是积分的速度要快而且必须实时。

1. we need some way to retrieve the scene’s radiance given any direction vector wi.
2. solving the integral needs to be fast and real-time.

now, the first requirement is relatively easy. we have already hinted it, but one way of representing an enviroment or scene’s irradiance is in the form of a (processed) enviroment cubemap.
given a such cubemap, we can visualize every texel of the cubemap as one simple emitting light source. by sampling this cubemap with any directoin vector wi we retrieve the scene’s radiance from that direction.
第一个问题好解决，就是提供一个立方体贴图，这个贴图有个术语名，叫做辐照度贴图。

getting the scene’s radiance given any direction vector wi is then simple as:

vec3 radiance = texture(_cubemapEnvironment, w_i).rgb;  

_cubemapEnvironment立方体贴图

有了辐照度贴图了，但是对于每个点进行渲染的时候，总不能采样所有的方向，这样太慢了，不现实，如何解决呢？考虑预计算。
still, solving the integral requires us to sample the enviroment map from not just one direction, but all possible directions wi over the hemisphere Ω which is far too expensive for each fragment shader invocation.
to solve the integral in a more efficient fashion we will want to pre-process or pre-compute most of its computations.
for this we will have to delve a bit deeper into the reflectance equation:

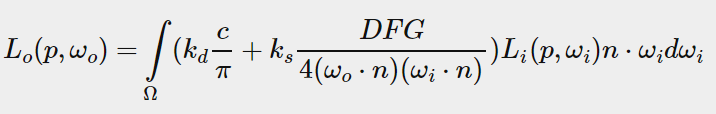
taking a good at the reflectance equation we find that the diffuse kd and specular ks term of the BRDF are independent from each other and we can split the integral in two:

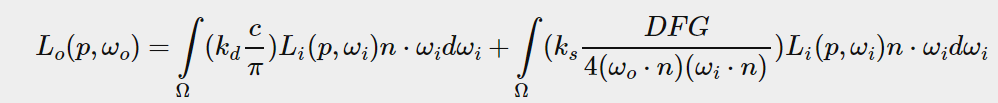
by splitting the integral in two parts we an focus on both the diffuse and specular term individually;
the focus of this tutorial being on the diffuse integral. 本节只介绍漫反射积分部分。

taking a closer look at the diffuse integral we find that the diffuse lambert term is a constant term (the color c, the refraction ratio kd and π are constant over the integral) and not dependent on any of the integral variables. given this, we can move the constant term out of the diffuse integral:

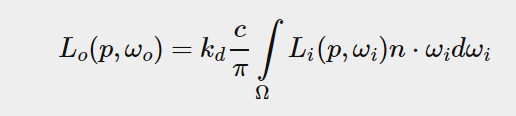
this gives us an integral that only depends on wi (assuming p is a the center of the environment map).
with this knowledge, we can calcualte or pre-compute a new cubemap that stores in each sample direction (or texel) wo the diffuse integral’s result by convolution. 卷积

convolution is applying some computation to each entry in a data set considering all other entries in the data set;
the data set being the scene’s radiance or environment map. thus for every sample direction in the cubemap, we take all other sample directions over the hemisphere Ω into account.

to convolute an environment map we solve the integral for each output wo sample direction by discretely sampling a large number of directions wi over the hemisphere Ω and averaging their radiance.
the hemisphere we build the sample directions wi from is oriented towards the output wo sample direction we are convoluting.
这句话不太好理解，我们可以尝试这么理解。
wo是颜色输出的方向，wi是光线输入的方向。
如何计算wo呢？是在半球上采样多个wi取平均值得到wo。而半球的方向是怎么确定的呢？是微表面的法线方向确定的。所以具体的代码可以看下面的做卷积的代码。必然和法线相关。

This pre-computed cubemap, that for each sample direction wo stores the integral result, can be thought of as the pre-computed sum of all indirect diffuse light of the scene hitting some surface aligned along direction wo. Such a cubemap is known as an irradiance map seeing as the convoluted cubemap effectively allows us to directly sample the scene’s (pre-computed) irradiance from any direction wo.

the radiance equation also depends on a position p, which we have assumed to be at the center of the irrdiance map. this does mean all diffuse indirect light must come from a single environment map which may break the illusion of reality (especially indoors). render engines solve this by palcing reflection probes 反射探针 all over the scene where each reflection probes calcualtes its own irradiance map of its surroudings. this way, the irrdiance (and radiacne) at position p is the interpolated irradiance between its closest reflection probes. for now, we assume we always sample the environment map from its center and discuss reflection probes in a later tutorial.

below is an example of a cubemap environment map and its resulting irradiance map (courtesy of wave engine), averaging the scene’s radiance for every direction wo .

by storing the convolued result in each cubemap texel (in the direction of wo) the irradiance map displays somewhat like an average color or lighting display of the environment. sampling any direction from this environment map will give us the scene’s irradiance from that particular direction.

PBR and HDR
we have briefly touched upon it in the lighting tutorial: taking the high dynamic range of your scene’s lighting into account in a PBR pipeline is incredibly 难以置信的 important. as PBR bases most of its inputs on real physical properties and mesurements it makes sense to closely match the incoming light values to their physical equivalents. whether we make educative guesses on each light’s radiant flux or use their direct physical equivalent, the difference between a simple light bulb or the sun is significant either way. without working in an HDR render environment it is impossible to correctly specify each light’s relative intensity.

So, PBR and HDR go hand in hand, but how does it all relate to image based lighting? We’ve seen in the previous tutorial that it’s relatively easy to get PBR working in HDR. However, seeing as for image based lighting we base the environment’s indirect light intensity on the color values of an environment cubemap we need some way to store the lighting’s high dynamic range into an environment map.

The environment maps we’ve been using so far as cubemaps (used as skyboxes for instance) are in low dynamic range (LDR). We directly used their color values from the individual face images, ranged between 0.0 and 1.0, and processed them as is. While this may work fine for visual output, when taking them as physical input parameters it’s not going to work.

The radiance HDR file format 辐射率HDR文件格式
Enter the radiance file format 进入辐射率文件格式. The radiance file format (with the .hdr extension) 辐射率格式文件，后缀是.hdr
stores a full cubemap with all 6 faces as floating point data 这个格式的文件存储了立方体贴图6个面的数据，数据都是浮点格式。
allowing anyone to specify color values outside the 0.0 to 1.0 range to give lights their correct color intensities. 允许我们存储超过0到1范围之外的数据，以保证正确的颜色强度。
The file format also uses a clever trick to store each floating point value not as a 32 bit value per channel, but 8 bits per channel using the color’s alpha channel as an exponent (this does come with a loss of precision). This works quite well, but requires the parsing program to re-convert each color to their floating point equivalent. 它的存储方法，不是每个通道32位，而是8位，但是使用透明通道作为指数。所以程序中要进行根绝浮点数表示法进行反推原来的数。

There are quite a few radiance HDR environment maps freely available from sources like sIBL archive of which you can see an example below:

This might not be exactly what you were expecting as the image appears distorted and doesn’t show any of the 6 individual cubemap faces of environment maps we’ve seen before. This environment map is projected from a sphere onto a flat plane such that we can more easily store the environment into a single image known as an equirectangular map. This does come with a small caveat as most of the visual resolution is stored in the horizontal view direction, while less is preserved in the bottom and top directions. In most cases this is a decent compromise as with almost any renderer you’ll find most of the interesting lighting and surroundings in the horizontal viewing directions.

HDR and stb_image.h
Loading radiance HDR images directly requires some knowledge of the file format which isn’t too difficult, but cumbersome nonetheless. Lucky for us, the popular one header library stb_image.h supports loading radiance HDR images directly as an array of floating point values which perfectly fits our needs. With stb_image added to your project, loading an HDR image is now as simple as follows:

#include "stb_image.h"
[...]stbi_set_flip_vertically_on_load(true);
int width, height, nrComponents;
float *data = stbi_loadf("newport_loft.hdr", &width, &height, &nrComponents, 0);
unsigned int hdrTexture;
if (data)
{glGenTextures(1, &hdrTexture);glBindTexture(GL_TEXTURE_2D, hdrTexture);glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB16F, width, height, 0, GL_RGB, GL_FLOAT, data); glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);stbi_image_free(data);
}
else
{std::cout << "Failed to load HDR image." << std::endl;
}  

stb_image.h automatically maps the HDR values to a list of floating point values: 32 bits per channel and 3 channels per color by default. This is all we need to store the equirectangular HDR environment map into a 2D floating point texture.

From Equirectangular to Cubemap 等距柱状投影到立方体贴图

It is possible to use the equirectangular map directly for environment lookups, but these operations can be relatively expensive in which case a direct cubemap sample is more performant 立方体贴图高性能. Therefore, in this tutorial we’ll first convert the equirectangular image to a cubemap for further processing. 所以我们先将equirectangular图片转换为立方体贴图. Note that in the process we also show how to sample an equirectangular map as if it was a 3D environment map in which case you’re free to pick whichever solution you prefer.

To convert an equirectangular image into a cubemap we need to render a (unit) cube and project the equirectangular map on all of the cube’s faces from the inside and take 6 images of each of the cube’s sides as a cubemap face. The vertex shader of this cube simply renders the cube as is and passes its local position to the fragment shader as a 3D sample vector:

#version 330 core
layout (location = 0) in vec3 aPos;out vec3 localPos;uniform mat4 projection;
uniform mat4 view;void main()
{localPos = aPos;  gl_Position =  projection * view * vec4(localPos, 1.0);
}

For the fragment shader we color each part of the cube as if we neatly folded the equirectangular map onto each side of the cube. To accomplish this, we take the fragment’s sample direction as interpolated from the cube’s local position and then use this direction vector and some trigonometry magic to sample the equirectangular map as if it’s a cubemap itself. We directly store the result onto the cube-face’s fragment which should be all we need to do:

#version 330 core
out vec4 FragColor;
in vec3 localPos;uniform sampler2D equirectangularMap;const vec2 invAtan = vec2(0.1591, 0.3183);
vec2 SampleSphericalMap(vec3 v)
{vec2 uv = vec2(atan(v.z, v.x), asin(v.y));uv *= invAtan;uv += 0.5;return uv;
}void main()
{		vec2 uv = SampleSphericalMap(normalize(localPos)); // make sure to normalize localPosvec3 color = texture(equirectangularMap, uv).rgb;FragColor = vec4(color, 1.0);
}

if u render a cube at the center of the scene given an HDR equirectangular map u will get sth. that looks like this:

this demontrates that we effectively mapped an equirectangular image onto a cubic shape, but does not yet help us in converting the source HDR image onto a cubemap texture. to accomplish this we have to render the same cube 6 times looking at each individual face of the cube while recording its visual result with a framebuffer object:

unsigned int captureFBO, captureRBO;
glGenFramebuffers(1, &captureFBO);
glGenRenderbuffers(1, &captureRBO);glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 512, 512);
glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, captureRBO);  

of course, we then also generate the corresponding cubemap, pre-allocating memory for each of its 6 faces:

unsigned int envCubemap;
glGenTextures(1, &envCubemap);
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);
for (unsigned int i = 0; i < 6; ++i)
{// note that we store each face with 16 bit floating point valuesglTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 512, 512, 0, GL_RGB, GL_FLOAT, nullptr);
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

then what is left to do is capture the equirectangular 2D texture onto the cubemap faces.

i will not go over the details as the code details topics previously discussed in the framebuffer and point shadows tutorials, but it effectively boils down to 归结为 setting up 6 different view matrices facing each side of the cube, given a projection matrix with a fov of 90 degrees to capture the entire face, and render a cube 6 times storing the results in a floating point framebuffer:

glm::mat4 captureProjection = glm::perspective(glm::radians(90.0f), 1.0f, 0.1f, 10.0f);
glm::mat4 captureViews[] = 
{glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 1.0f,  0.0f,  0.0f), glm::vec3(0.0f, -1.0f,  0.0f)),glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(-1.0f,  0.0f,  0.0f), glm::vec3(0.0f, -1.0f,  0.0f)),glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f,  1.0f,  0.0f), glm::vec3(0.0f,  0.0f,  1.0f)),glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f, -1.0f,  0.0f), glm::vec3(0.0f,  0.0f, -1.0f)),glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f,  0.0f,  1.0f), glm::vec3(0.0f, -1.0f,  0.0f)),glm::lookAt(glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3( 0.0f,  0.0f, -1.0f), glm::vec3(0.0f, -1.0f,  0.0f))
};// convert HDR equirectangular environment map to cubemap equivalent
equirectangularToCubemapShader.use();
equirectangularToCubemapShader.setInt("equirectangularMap", 0);
equirectangularToCubemapShader.setMat4("projection", captureProjection);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, hdrTexture);glViewport(0, 0, 512, 512); // don't forget to configure the viewport to the capture dimensions.
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
for (unsigned int i = 0; i < 6; ++i)
{equirectangularToCubemapShader.setMat4("view", captureViews[i]);glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, envCubemap, 0);glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);renderCube(); // renders a 1x1 cube
}
glBindFramebuffer(GL_FRAMEBUFFER, 0); 

we take the color attachment of the framebuffer and switch its texture target around for every face of the cubemap, directly rendering the scene into one of cubemap’s faces. once this routine 程序 has finished (which we only have to do once) the cubemap envCubemap should be the cubemapped environment version of our original HDR image.

let us test the cubemap by writing a very simple skybox shader to display the cubemap around us:

#version 330 core
layout (location = 0) in vec3 aPos;uniform mat4 projection;
uniform mat4 view;out vec3 localPos;void main()
{localPos = aPos;mat4 rotView = mat4(mat3(view)); // remove translation from the view matrixvec4 clipPos = projection * rotView * vec4(localPos, 1.0);gl_Position = clipPos.xyww;
}

note the xyww trick here that ensures the depth value of the rendered cube fragments always end up at 1.0, the maximum depth value, as described in the cubemap tutorial. 这个要复习下。do note that we need to change the depth comparison function to GL_LEQUAL:

glDepthFunc(GL_LEQUAL);  

the fragment shader then directly sampels the cubemap environment map using the cube’s local fragment position:

#version 330 core
out vec4 FragColor;in vec3 localPos;uniform samplerCube environmentMap;void main()
{vec3 envColor = texture(environmentMap, localPos).rgb;envColor = envColor / (envColor + vec3(1.0));envColor = pow(envColor, vec3(1.0/2.2)); FragColor = vec4(envColor, 1.0);
}

we sample the environment map using its interpolated vertex cube positions that directly coorespond to the correct direction vector to sample. seeing as the camera’s translation components are ignored, rendering this shader over a cube should give u the environment map as a non-moving background. also, note that as we directly output the environment map’s HDR values to the default LDR framebuffer we want to properly tone map the color values. furthermore, almost all HDR maps are in linear color space by default so we need to apply gamma correction before writing to the default framebuffer.

now rendering the sampled environment map over the previously rendered spheres should look sth. like this:

well… it took us quite a bit of setup to get here, but we successfully managed to read an HDR environment map, convert it from its equirectangular mapping to a cubemap and render the HDR cubemap into the scene as a skybox. furthermore, we set up a small system to render onto all 6 faces of a cubemap which we will need again when convoluting the environment map. u can find the source code of the entire conversion process here.

cubemap convolution
as described at the start of the tutorial,
our main goal is to solve the integral for all diffuse indirect lighting
given the scene’s irradiance in the form of a cubemap environment map.
we know that we can get the radiance of the scene L(p,wi) in a particular direction by sampling an HDR environment map in direction wi. to solve the integral, we have to sample the scene’s radiance from all possible directions within the hemisphere Ω for each fragment.
it is however computationally impossible to sample the environment’s lighting from every possible direction in Ω, the number of possible directions is theoretically infinite.
we can however, approximate the number of directions by taking a finite number of directions or samples,
spaced uniformly or taken randomly from within the hemisphere to get a fairly accurate approximate of the irradiance, effectively solving the integral ∫ discretely.

it is however still too expensive to do this for every fragment in real-time
as the number of samples still needs to be significantly large for decent results,
so we want to pre-compute this. since the orientation of the hemisphere decides where we capture the irradiance
we can pre-calcualte the irradiance for every possible hemisphere orientation oriented around all outgoing directions wo:

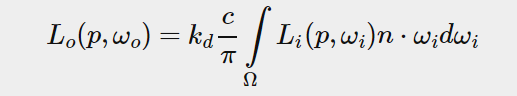
given any direction vector wi, we can then sample the pre-computed irradiance map to retrieve the total diffuse irradiance from direction wi. to determine the amount of indirect diffuse (irradiant) light at a fragment surface,
we retrieve the total irradiance from the hemisphere oriented around its surface’s normal.
obtaining the scene’s irradiance is then as simple as:

vec3 irradiance = texture(irradianceMap, N);

now, to generate the irradiance map we need to convolute the environment’s lighting as converted to a cubemap.
given that for each fragment the surfaces’s hemisphere is oriented along the normal vector N, convoluting a cubemap equals calculating the total averaged radiance of each direction wi in the hemisphere Ω oriented along N.

thankfully, all of the cumbersome setup in this tutorial is not all for nothing as we can now directly take the converted cubemap, convolute it in a fragment shader and capture its result in a new cubemap using a framebuffer that renders to all 6 face directions. as we have already set this up for converting the equirectangular environment map to a cubemap, we can take the exact sampe approach but use a different fragment shader:

#version 330 core
out vec4 FragColor;
in vec3 localPos;uniform samplerCube environmentMap;const float PI = 3.14159265359;void main()
{		// the sample direction equals the hemisphere's orientation vec3 normal = normalize(localPos);vec3 irradiance = vec3(0.0);[...] // convolution codeFragColor = vec4(irradiance, 1.0);
}

with environmentMap being the HDR cubemap as converted from the equirectangular HDR environment map.

there are many ways to convolute the environment map,
but for this tutorial we are going to generate a fixed amount of sample vectors for each cubemap texel along a hemisphere Ω oriented around the sample direction and average the results. the fixed amount of sample vectors will be uniformly spread inside the hemisphere. note that an integral is a continuous function and discretely sampling its function given a fixed amount of sample vectors will be an approximation.
the more sample vectors we use, the better we approximate the integral.
The integral ∫ of the reflectance equation revolves around the solid angle dw which is rather difficult to work with. Instead of integrating over the solid angle dw we’ll integrate over its equivalent spherical coordinates θ and ϕ.

we use the polar azimuth 方位 ϕ angle to sample around the ring of the hemisphere between 0 and 2π, and use the inclination zenith θ 仰角 angle between 0 and 0.5π to sample the increasing rings of the hemisphere. this will give us the updated reflectance integral:

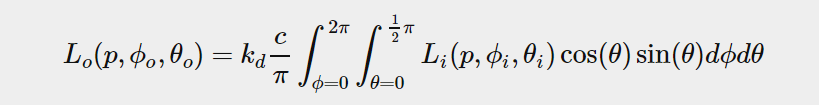
solving the integral requires us to take a fixed number of discrete samples within the hemisphere Ω and averaging their results. this translates the integral to the following discrete version as based on the Riemann sum given n1 and n2 discrete samples on each spherical coordinate respectively:

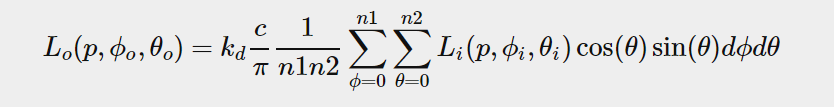
as we sample both spherical values discretely, each sample will approximate or average an area on the hemisphere as the image above shows.
note that (due to the general properties of a spherical shape) the hemisphere’s discrete sample area gets smaller the higher the zenith angle θ as the sample regions converge towards the center top. to compensate for the smaller areas, we weigh its contribution by scaling the area by sinθ clarifying the added sin.

Discretely sampling the hemisphere given the integral’s spherical coordinates for each fragment invocation translates to the following code:

vec3 irradiance = vec3(0.0);  vec3 up    = vec3(0.0, 1.0, 0.0);
vec3 right = cross(up, normal);
up         = cross(normal, right);float sampleDelta = 0.025;
float nrSamples = 0.0; 
for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta)
{for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta){// spherical to cartesian (in tangent space)vec3 tangentSample = vec3(sin(theta) * cos(phi),  sin(theta) * sin(phi), cos(theta));// tangent space to worldvec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N; irradiance += texture(environmentMap, sampleVec).rgb * cos(theta) * sin(theta);nrSamples++;}
}
irradiance = PI * irradiance * (1.0 / float(nrSamples));

we specify a fixed sampleDelta delta value to traverse the hemisphere; decreasing or increasing the sample delta will increase or decrease the accuracy respectively.

From within both loops, we take both spherical coordinates to convert them to a 3D Cartesian sample vector, convert the sample from tangent to world space and use this sample vector to directly sample the HDR environment map. We add each sample result to irradiance which at the end we divide by the total number of samples taken, giving us the average sampled irradiance. Note that we scale the sampled color value by cos(theta) due to the light being weaker at larger angles and by sin(theta) to account for the smaller sample areas in the higher hemisphere areas.

Now what’s left to do is to set up the OpenGL rendering code such that we can convolute the earlier captured envCubemap. First we create the irradiance cubemap (again, we only have to do this once before the render loop):

unsigned int irradianceMap;
glGenTextures(1, &irradianceMap);
glBindTexture(GL_TEXTURE_CUBE_MAP, irradianceMap);
for (unsigned int i = 0; i < 6; ++i)
{glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB16F, 32, 32, 0, GL_RGB, GL_FLOAT, nullptr);
}
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

as the irradiance map averages all surrouding radiance uniformly it does not have a lot of high frequency details
so we can store the map at a low resolution (32x32) and let opengl’s linear filtering do most of the work. next, we re-scale the capture framebuffer to the new resolution:

glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
glBindRenderbuffer(GL_RENDERBUFFER, captureRBO);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT24, 32, 32);  

Using the convolution shader we convolute the environment map in a similar way we captured the environment cubemap:

irradianceShader.use();
irradianceShader.setInt("environmentMap", 0);
irradianceShader.setMat4("projection", captureProjection);
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_CUBE_MAP, envCubemap);glViewport(0, 0, 32, 32); // don't forget to configure the viewport to the capture dimensions.
glBindFramebuffer(GL_FRAMEBUFFER, captureFBO);
for (unsigned int i = 0; i < 6; ++i)
{irradianceShader.setMat4("view", captureViews[i]);glFramebufferTexture2D(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, irradianceMap, 0);glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);renderCube();
}
glBindFramebuffer(GL_FRAMEBUFFER, 0);  

now after this routine we should have a pre-computed irradiance map that we can directly use for our diffuse image based lighting. to see if we successfully convoluted the environment map let us substitute the environment map for the irradiance map as the skybox’s environment sampler:

if it looks like a heavily blurred version of the environment map u have successfully convoluted the environment map.

PBR and indirect irradiance lighting
the irradiance map represents the diffuse part of the reflectance integral as accumulated from all surrounding indirect light.
Seeing as the light doesn’t come from any direct light sources, but from the surrounding environment we treat both the diffuse and specular indirect lighting as the ambient lighting, replacing our previously set constant term.

First, be sure to add the pre-calculated irradiance map as a cube sampler:

uniform samplerCube irradianceMap;

Given the irradiance map that holds all of the scene’s indirect diffuse light, retrieving the irradiance influencing the fragment is as simple as a single texture sample given the surface’s normal:

// vec3 ambient = vec3(0.03);
vec3 ambient = texture(irradianceMap, N).rgb;

However, as the indirect lighting contains both a diffuse and specular part as we’ve seen from the split version of the reflectance equation we need to weigh the diffuse part accordingly.
Similar to what we did in the previous tutorial we use the Fresnel equation to determine the surface’s indirect reflectance ratio from which we derive the refractive or diffuse ratio:

vec3 kS = fresnelSchlick(max(dot(N, V), 0.0), F0);
vec3 kD = 1.0 - kS;
vec3 irradiance = texture(irradianceMap, N).rgb;
vec3 diffuse    = irradiance * albedo;
vec3 ambient    = (kD * diffuse) * ao; 

As the ambient light comes from all directions within the hemisphere oriented around the normal N there’s no single halfway vector to determine the Fresnel response.
To still simulate Fresnel, we calculate the Fresnel from the angle between the normal and view vector. However, earlier we used the micro-surface halfway vector, influenced by the roughness of the surface, as input to the Fresnel equation. As we currently don’t take any roughness into account, the surface’s reflective ratio will always end up relatively high. Indirect light follows the same properties of direct light so we expect rougher surfaces to reflect less strongly on the surface edges. As we don’t take the surface’s roughness into account, the indirect Fresnel reflection strength looks off on rough non-metal surfaces (slightly exaggerated for demonstration purposes):

We can alleviate the issue by injecting a roughness term in the Fresnel-Schlick equation as described by Sébastien Lagarde:

vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness)
{return F0 + (max(vec3(1.0 - roughness), F0) - F0) * pow(1.0 - cosTheta, 5.0);
}   

by taking account of the surface’s roughness when calculating the fresnel response, the ambient code ends up as:

vec3 kS = fresnelSchlickRoughness(max(dot(N, V), 0.0), F0, roughness); 
vec3 kD = 1.0 - kS;
vec3 irradiance = texture(irradianceMap, N).rgb;
vec3 diffuse    = irradiance * albedo;
vec3 ambient    = (kD * diffuse) * ao; 

As you can see, the actual image based lighting computation is quite simple and only requires a single cubemap texture lookup; most of the work is in pre-computing or convoluting the environment map into an irradiance map.

If we take the initial scene from the lighting tutorial where each sphere has a vertically increasing metallic and a horizontally increasing roughness value and add the diffuse image based lighting it’ll look a bit like this:

It still looks a bit weird as the more metallic spheres require some form of reflection to properly start looking like metallic surfaces (as metallic surfaces don’t reflect diffuse light) which at the moment are only coming (barely) from the point light sources.
Nevertheless, you can already tell the spheres do feel more in place within the environment (especially if you switch between environment maps) as the surface response reacts accordingly to the environment’s ambient lighting.

You can find the complete source code of the discussed topics here. In the next tutorial we’ll add the indirect specular part of the reflectance integral at which point we’re really going to see the power of PBR.

Further reading
Coding Labs: Physically based rendering: an introduction to PBR and how and why to generate an irradiance map. http://www.codinglabs.net/article_physically_based_rendering.aspx
The Mathematics of Shading: a brief introduction by ScratchAPixel on several of the mathematics described in this tutorial, specifically on polar coordinates and integrals.
https://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/mathematics-of-shading?url=mathematics-physics-for-computer-graphics/mathematics-of-shading