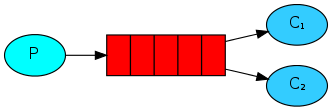
本文主要是介绍Point Processes and Queues,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. Martingales (鞅)
1.1 Histories of probability space
( Ω , F , P ) (\Omega,\mathcal{F},P) (Ω,F,P) probability space
( X t , t ≥ 0 ) (X_t, t\ge 0) (Xt,t≥0) stochastic process
定义. 随机变量生产的 σ \sigma σ-代数:In association with such a process X t X_t Xt, we define for each t ≥ 0 t\ge 0 t≥0 a sub- σ \sigma σ-filed of F \mathcal{F} F, denoted F t X \mathcal{F}_t^{X} FtX, by
F t X = σ ( X s , s ∈ [ 0 , t ] ) \mathcal{F}_t^{X} = \sigma(X_s, s\in[0,t]) FtX=σ(Xs,s∈[0,t])
举例:随机变量生成的 σ \sigma σ-代数,指的是一组特殊事件组成的集合:这些事件是否发生,可以通过随机变量的取值明确判断出来。举个例子吧。
比如今天可能下雨也可能不下,下雨时随机变量 X = 1 X=1 X=1,反之 X = 0 X=0 X=0。然而,下不下雨只是“今天”的一个属性,其它属性,比如我早饭吃的是火腿还是培根,也是全世界所包含的信息的一部分。
假设整个概率空间由下面这些元素组成:
[火腿,下雨]:概率0.25,X = 1
[火腿,不下雨]:概率0.25,X = 0
[培根,下雨]:概率0.25,X = 1
[培根,不下雨]:概率0.25,X = 0
这时,X生成的代数包括下面三个非空集合:
{X = 1} = {[火腿,下雨],[培根,下雨]}
{X = 0} = {[火腿,不下雨],[培根,不下雨]}
{X = 0或1} = {[火腿,不下雨],[培根,不下雨],[火腿,下雨],[培根,下雨]}
可见不管X=1还是0,我都既有可能吃火腿,也有可能吃培根;从X的取值里,你得不到任何关于我早饭吃了什么的信息。因此“早饭吃培根”这一事件,就被排除在X生成的代数之外了。具体来说:早饭吃培根 = {{培根,下雨},{培根,不下雨}},不属于X生成的代数。
定义. Let Y Y Y be a R k \mathbb{R}^k Rk- valued process such that for each t ≥ 0 t\ge 0 t≥0, Y t Y_t Yt is F t X \mathcal{F}_t^X FtX-measurable, a well-known representation result on measurability states that
Y = ϕ ( X s , s ∈ S ) Y=\phi(X_s,s\in S) Y=ϕ(Xs,s∈S) where S S S is a countable subset of [ 0 , t ] [0,t] [0,t] and ϕ \phi ϕ is a borelian function(Borel函数) from R n ∣ S ∣ \mathbb{R}^{n|S|} Rn∣S∣ into R k \mathbb{R}^k Rk.
We say Y t Y_t Yt is adapted to F t X \mathcal{F}_t^X FtX, if
Y t = ψ t ( X 0 t ) Y_t=\psi_t(X_0^t) Yt=ψt(X0t) for some ψ t \psi_t ψt, i.e., Y t Y_t Yt depends causally on X t X_t Xt.
If F t ⊇ F t X \mathcal{F}_t\supseteq\mathcal{F}_t^X Ft⊇FtX, then F t \mathcal{F}_t Ft is called a history of X t X_t Xt, and X t X_t Xt is adapted to F t \mathcal{F}_t Ft.
定义. 停时(stopping time) 一类随机时刻,指具有某种与将来无关性质的随机时刻。给定概率空间 ( Σ , F , P ) (\Sigma,\mathcal{F},P) (Σ,F,P)及其滤子 F t \mathcal{F}_t Ft,映射 τ : Σ → T ∪ { ∞ } \tau:\Sigma→T\cup\{\infty\} τ:Σ→T∪{∞},如果对任意的 t ∈ I t∈I t∈I, { ω : ω ∈ Σ , τ ( ω ) ≤ t } ∈ F t \{\omega:\omega\in\Sigma,τ(ω)≤t\}\in\mathcal{F}_t {ω:ω∈Σ,τ(ω)≤t}∈Ft,则称映射 τ \tau τ为一个 F t \mathcal{F}_t Ft停时。
1.2 Martingale
A history is given on the probability space ( Ω , F , P ) (\Omega,\mathcal{F},P) (Ω,F,P). A ( P , F t ) (P,\mathcal{F}_t) (P,Ft)-martingale over [ 0 , c ] [0,c] [0,c] is a real-valued stochastic process X t X_t Xt such that:
(1) X t X_t Xt is adapted to F t \mathcal{F}_t Ft,
(2) X t X_t Xt is P P P-integrable, i.e., E [ ∣ X t ∣ ] < ∞ , ∀ t ∈ [ 0 , c ] E[|X_t|]<\infty,\forall t\in[0,c] E[∣Xt∣]<∞,∀t∈[0,c]
(3) for all 0 ≤ s ≤ t ≤ c 0\leq s\leq t\leq c 0≤s≤t≤c, E [ X t ∣ F s ] = X s E[X_t|\mathcal{F}_s]=X_s E[Xt∣Fs]=Xs, P − a . s P-a.s P−a.s (almost surely).
1.3 Levy Formula
Let X t X_t Xt be a right-continuous N + N_+ N+-valued F t \mathcal{F}_t Ft-Markov chain which is stable and conservative and admits the Q Q Q-matrix ( q i j : i , j ∈ N + ) (q_{ij}:i,j\in N_+) (qij:i,j∈N+). If f f f is a nonnegative function from N + × N + N_+\times N_+ N+×N+ into R + R_+ R+, then for any 0 ≤ s ≤ t 0\leq s\leq t 0≤s≤t, the Levy formulat holds:
E [ ∑ s < u ≤ t f ( X u − , X u ) ∣ σ ( X s ) ] = E [ ∫ s t ∑ j ≠ X u q X u j f ( X u , j ) d u ∣ σ ( X s ) ] E\left[ \mathop{\sum}\limits_{s<u\leq t} f(X_{u^-},X_u) \Big| \sigma(X_s) \right] = E\left[ \int_s^t \mathop{\sum}\limits_{j\neq X_u} q_{X_uj} f(X_u, j) du \Big| \sigma(X_s) \right] E[s<u≤t∑f(Xu−,Xu)∣∣∣σ(Xs)]=E⎣⎡∫stj=Xu∑qXujf(Xu,j)du∣∣∣σ(Xs)⎦⎤
1.4 Radon-Nikodyn Derivatives (likeihood ratios)
Let P P P and Q Q Q be two probability measures defined on the same measurable space ( Σ , F ) (\Sigma,\mathcal{F}) (Σ,F), and let F t \mathcal{F}_t Ft be a history. For each t ≥ 0 t\ge 0 t≥0, denote by P t P_t Pt and Q t Q_t Qt the restrictions of P P P and Q Q Q to F t \mathcal{F}_t Ft respectively. Suppose that for some c ≥ 0 c\ge 0 c≥0, Q c Q_c Qc is absolutely continuous with respect to P c P_c Pc. Then clearly, for all t ∈ [ 0 , c ] t\in[0,c] t∈[0,c], Q t Q_t Qt is absolutely continuous with respect to P t P_t Pt. Define
L t : = d Q t d P t L_t := \frac{dQ_t}{dP_t} Lt:=dPtdQt to be the Radon-Nikodym derivation of Q t Q_t Qt with respect to P t P_t Pt.
Proposition. L t L_t Lt is a ( P , F t ) (P,\mathcal{F}_t) (P,Ft)-martingale over [ 0 , c ] [0,c] [0,c].
1.5 Predictability
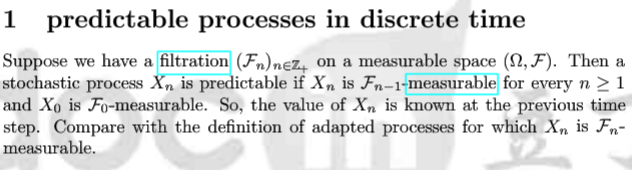



Exercise. Given a stopping time τ \tau τ, let
I n = { 1 , if n ≤ τ 0 , if n > τ I_n = \begin{cases} 1, & \text{if }n\leq\tau \\ 0, & \text{if }n>\tau \end{cases} In={1,0,if n≤τif n>τ Show that ( I n ) n ≥ 1 (I_n)_{n\ge 1} (In)n≥1 is a predictable process.
2. Girsanov Theorem
定理1. If P P P and Q Q Q are equivalent measures, and X t X_t Xt is an F t \mathcal{F}_t Ft-adpated process then the following results hold:
E Q ( X t ) = E P ( X t d Q d P ) E_Q(X_t)=E_P\left(X_t\frac{dQ}{dP}\right) EQ(Xt)=EP(XtdPdQ)
这篇关于Point Processes and Queues的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!