统计教程｜PASS实现单因素二元Logistic回归分析且自变量为二分类的优势比检验的样本量估计

本文主要是介绍统计教程｜PASS实现单因素二元Logistic回归分析且自变量为二分类的优势比检验的样本量估计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在对临床数据的探索分析工作中，我们经常会使用Logistic回归分析去探索影响疾病的发生、发展的重要影响因素，或应用Logistic回归模型进行相关的预测分析。但是在进行Logistic回归分析时，样本含量的估计常常是令临床科研工作者最头痛的一件事了。常常纠结选哪些作为自变量或选多少个合适，因为大家通常采取的办法是选取研究中拟纳入的协变量个数的10～15倍（也有教科书上指出：经验上病例和对照的人数应该至少各有30~50例）作为样本含量的估计值。但大家应该注意，这个条件仅满足了多因素Logistic回归分析时数学运算所需的最低要求，这并不能保证足够的检验效能；此外，当研究设计阶段对协变量信息认识不全面时，也给样本含量的估计带来了困难。

由于Logistic回归主要描述了因变量和自变量间的一种非线性的关系，在进行Logistic回归分析的样本量估算时应根据其各自不同的适用条件选取不同的估算公式。不同的软件采用的样本量计算公式有所差异PASS软件作为功能强大的样本量计算软件，针对多种Logistic回归分析的都有针对的模块可进行计算，今天我们主要讲解PASS15.0软件实现当自变量为二分类的单因素二元Logistic回归分析时其优势比Wald检验的样本量估计。在PASS15.0软件中使用的是Demidenko等人2007年提出的近似公式，当只有一个自变量（假设该自变量为X）且为二分类变量时（X=0表示未发生，X=1表示发生），其主要的计算公式如下：

其中`P=（1-R）P0+ R（P1），即研究对象中Y=1的比例。

公式中，N为所需的样本含量，P0为X=0时Y=1的发生率，P1为X=1时Y=1的发生率（有时我们只知道OR，此时我们可根据：

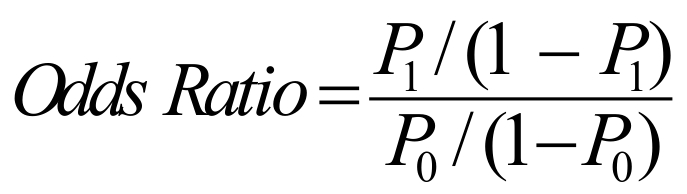
得到：

但是在PASS15软件中可选择直接采用OR值进行计算），R为研究对象中X=1的比例，Z1-α/2表示标准正态分布的第1-α/2分位数或双侧α界值、Z1-β表示标准正态分布的第1-β分位数或单侧β界值，Z1-α/2和Z1-β均可通过查阅Z值表获得。

下面我们在本节将主要讲解采用PASS15.0软件实现当只有一个二分类变量时单因素二元Logistic回归分析时其优势比Wald检验所需样本含量估计方法。

例：假设某妇产科医生想研究同型半胱氨酸（HCY）与早产的关系，有报道表明，当孕妇血浆中HCY＜12.4μmol/L时发生率为0.06，HCY≥12.4μmol/L时发生率为0.18，假定孕妇中HCY≥12.4μmol/L的人群占比为7%，α=0.05（双侧检验），β=0.20，问需要调查多少研究对象？

解析：本例严格来说应属于调查研究，其主要结局指标是是否发生早产，为二分类变量，主要研究因素（X）为孕妇的HCY是否≥12.4μmol/L，主要目的是研究HCY的水平与早产发生的关系，故我们可采用单因素Logistic回归分析两者的因果关系，可采用协变量为二分类变量的单因素二元Logistic回归分析的计算公式进行样本含量估算。本例共确定了五个参数：①α=0.05（双侧检验）；②检验效能（1-β）=0.8；③X=0时Y=1的发生率（P0）=0.06，④X=1时Y=1的发生率（P1）=0.18；⑤研究对象中X=1的比例 R=7%。

PASS软件样本含量估算的具体步骤：

01 PASS主菜单进入样本含量估算设置界面：

打开PASS15软件，①点击Regression菜单并双击或其前面的“＋”展开子菜单栏；→②点击Logistic Regression菜单并双击或其前面的“＋”展开子菜单栏；→③点击Binary X（Wald Test）；→④点击Tests for the Odds Ratio in Logistic Regression with One Binary X（Wald Test）→弹出Tests for the Odds Ratio in Logistic Regression with One Binary X（Wald Test）对话框进入单因素二元Logistic回归分析的样本含量估计界面，详见操作示意图（图1）。

02 PASS样本含量估算参数设置：

①Solve For：Sample Size，首先说明我们本次所求的结果为样本含量；→②Alternative Hypothesis：Two-Sided，表明进行双侧检验；→③Power：0.8，表明检验效能（1-β）为80%；→④Alpha：0.05，表示检验水准为0.05；→⑤P0[Pr（Y=1|X=0）]：0.06 ，指定X=0时Y=1的发生概率，即本例当HCY＜12.4μmol/L时发生早产的概率为0.06；→⑥Use P1 or ORyx：P1，指定采用指标P1还是ORyx估算样本量（P1和ORyx可根据相关公式相互转换），由于本例知道了P1的取值，故本例选择采用P1估算样本量；→⑦P1[Pr（Y=1|X=1）]：0.18，指定X=1时Y=1的发生概率，即本例当HCY≥12.4μmol/L时发生早产的概率为0.18；→⑧Percent with X=1：7，指定研究对象中X=1的比例，即本例中孕妇人群中HCY≥12.4μmol/L的患者比例大约占总人群的7%；→⑨击Calculate按钮，完成单因素二元Logistic回归分析的样本含量估算，详见操作示意图（图2）。

03 PASS样本含量估算结果：

由图3可知，PASS软件给出的自变量为二分类的单因素二元Logistic回归分析样本含量估算结果主要有：样本含量估算的结果、相关参考文献、样本量估算报告中出现各名词的定义、对计算结果的总结描述以及假定脱落率为20%时所需的样本含量估计结果和其各名词的相关定义。由于脱落率不同研究结果各不相同，故本次不看脱落率为20%的相关结果，我们主要关注N这一结果即可：本研究最少需要596例孕妇作为研究对象才可能得出HCY含量高低与早产的发生有显著相关的结论。