本文主要是介绍基尼不纯度:如何用它建立决策树?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
全文共1031字,预计学习时长3分钟

图源:unsplash
决策树是机器学习中使用的最流行和功能最强大的分类算法之一。顾名思义,决策树用于根据给定的数据集做出决策。也就是说,它有助于选择适当的特征以将树分成类似于人类思维脉络的子部分。
为了有效地构建决策树,我们使用了熵/信息增益和基尼不纯度的概念。让我们看看什么是基尼不纯度,以及如何将其用于构建决策树吧。
什么是基尼不纯度?
基尼不纯度是决策树算法中用于确定根节点的最佳分割以及后续分割的方法。这是拆分决策树的最流行、最简单的方法。它仅适用于分类目标,因为它只执行二进制拆分。
基尼不纯度的公式如下:
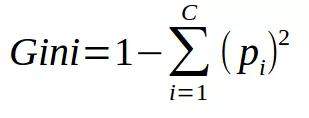
基尼不纯度越低,节点的同质性越高。纯节点(相同类)的基尼不纯度为零。以一个数据集为例,计算基尼不纯度。
该数据集包含18个学生,8个男孩和10个女孩。根据表现将他们分类如下:
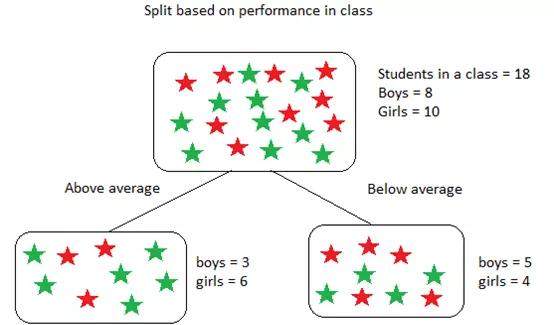
上述基尼不纯度的计算如下:
这篇关于基尼不纯度:如何用它建立决策树?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








