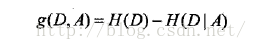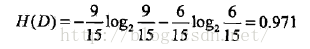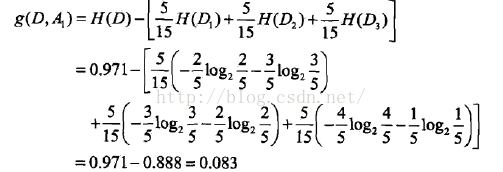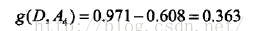本文主要是介绍决策树的实现原理与matlab代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
很久不写博客了,感觉很长一段时间只是一味的看书,疏不知一味地看书、写代码会导致自己的思考以及总结能力变得衰弱。所以,我决定还是继续写博客。废话不多说了,今天想主要记录数据挖掘中的决策树。希望能够将自己的理解写得通俗易懂。
决策树是一种对实例分类的树形结构,树中包含叶子节点与内部节点。内部节点主要是数据中的某一特性,叶子节点是根据数据分析后的最后结果。
先看一组数据:
这组数据的特性包含年龄、工作与否、是否有房、信贷情况以及最终分类结果贷款是否成功,共包含15组样例。
构建数的形状可以有多种,如下:

如果随意构建树,那将会导致有的构建树比较庞大,分类时代价比较大,有的构建树比较小,分类代价小。
比如针对是否有房这一列,发现如果样本有房这一列为是,最终分类结果便是可以贷款,而不需要判断其他的特性,便可以获得最终部分分类结果。
因此,构建树需要以最小的代价实现最快的分类。根据何种标准进行判别呢?
在信息论与概率统计中,熵是表示随机变量不确定的量度,设x是一个取有限个值的离散随机变量,其概率分布为:
则随机变量x的熵定义为
熵越大,其不确定性越大。
随机变量x在给定条件y下的条件熵为H(y|x);
信息增益表示得知特征x的信息而使得y类信息的不确定减少的程度。
因此,特征A对训练集D的信息增益g(D,A),定义为集合D的熵H(D)与特征A给定条件下D的条件熵H(D|A)之差,即
对表5.1给定的训练数据集D,计算各特征对其的信息增益,分别以A1,A2,A3,A4表示年龄,有工作,有自己的房子和信贷情况四个特征,则
(1)
(2)
这里D1,D2,D3分别是D中A1取为青年、中年、老年的样本子集,同理,求得其他特征的信息增益:
接下来根据之前的信息增益,对决策树进行生成,这里主要使用ID3算法,C4.5算法与之类似,只是将信息增益衡量转为信息增益比衡量。
主要方法如下:
从根节点开始,对节点计算所有可能的特征的信息增益,选择信息增益最大的特征作为该节点的特征,由该特征的不同取值建立子节点,再对子节点递归调用以上方法,构建决策树。
那么递归何时停止呢?当训练集中所有实例属于同一类时,或者所有特征都选择完毕时,或者信息增益小于某个阈值时,则停止递归,。
举例来说,根据之前对表5.1的熵的计算,由于A3(是否有自己的房子)信息增益最大,所以以A3为决策树的根节点的特征,它将数据集分为两个子集D1(A3取是)和D2(A3取否),由于D1的分类结果都是可以贷款,所以它成为叶节点,对于D2,则从特征A1,A2,A4这三个特征中重新选择特征,计算各个特征的信息增益:
因此选择A2作为子树节点,针对A2是否有工作这个特征,根据样本分类结果发现有工作与无工作各自的样本都属于同一类,因此将有工作与无工作作为子树的叶节点。这样便生成如下的决策树:
决策树生成算法递归的产生决策树,往往对训练数据分类准确,但对未知数据却没那么准确,即会出现过拟合状况。解决这个问题可以通过决策树的剪枝,让决策树简化。本文暂不对决策树的剪枝进行详细描述。
接下来,即对决策树实现的matlab代码:
1、首先,定义决策树的数据结构
tree
{
int pro //是叶节点(0表示)还是内部节点(1表示)
int value //如果是叶节点,则表示具体的分类结果,如果是内部节点,则表示某个特征
int parentpro //如果该节点有父节点,则该值表示父节点所表示特征的具体属性值
tree child[] //表示该节点的子树数组
}
2、根据训练集数据通过递归形成树:
function tree = maketree(featurelabels,trainfeatures,targets,epsino)
tree=struct('pro',0,'value',-1,'child',[],'parentpro',-1);
[n,m] = size(trainfeatures); %where n represent total numbers of features,m represent total numbers of examples
cn = unique(targets);%different classes
l=length(cn);%totoal numbers of classes
if l==1%if only one class,just use the class to be the lable of the tree and return
tree.pro=0;%reprensent leaf
tree.value = cn;
tree.child=[];
return
end
if n==0% if feature number equals 0
H = hist(targets, length(cn)); %histogram of class
[ma, largest] = max(H); %ma is the number of class who has largest number,largest is the posion in cn
tree.pro=0;
tree.value=cn(largest);
tree.child=[];
return
end
pnode = zeros(1,length(cn));
%calculate info gain
for i=1:length(cn)
pnode(i)=length(find(targets==cn(i)))/length(targets);
end
H=-sum(pnode.*log(pnode)/log(2));
maxium=-1;
maxi=-1;
g=zeros(1,n);
for i=1:n
fn=unique(trainfeatures(i,:));%one feature has fn properties
lfn=length(fn);
gf=zeros(1,lfn);
fprintf('feature numbers:%d\n',lfn);
for k=1:lfn
onefeature=find(fn(k)==trainfeatures(i,:));%to each property in feature,,calucute the number of this property
for j=1:length(cn)
oneinonefeature=find(cn(j)==targets(:,onefeature));
ratiofeature=length(oneinonefeature)/length(onefeature);
fprintf('feature %d, property %d, rationfeature:%f\n',i, fn(k),ratiofeature);
if(ratiofeature~=0)
gf(k)=gf(k)+(-ratiofeature*log(ratiofeature)/log(2));
end
end
ratio=length(onefeature)/m;
gf(k)=gf(k)*ratio;
end
g(i)=H-sum(gf);
fprintf('%f\n',g(i));
if g(i)>maxium
maxium=g(i);
maxi=i;
end
end
if maxium<epsino
H = hist(targets, length(cn)); %histogram of class
[ma, largest] = max(H); %ma is the number of class who has largest number,largest is the posion in cn
tree.pro=0;
tree.value=cn(largest);
tree.child=[];
return
end
tree.pro=1;%1 represent it's a inner node,0 represents it's a leaf
tv=featurelabels(maxi);
tree.value=tv;
tree.child=[];
featurelabels(maxi)=[];
%split data according feature
[data,target,splitarr]=splitData(trainfeatures,targets,maxi);
%tree.child=zeros(1,length(data));
%build child tree;
fprintf('split data into %d\n',length(data));
for i=1:length(data)
disp(data(i));
fprintf('\n');
disp(target(i));
fprintf('\n');
end
fprintf('\n');
for i=1:size(data,1)
result = zeros(size(data{i}));
result=data{i};
temptree=maketree(featurelabels,result,target{i},0);
tree.pro=1;%1 represent it's a inner node,0 represents it's a leaf
tree.value=tv;
tree.child(i)=temptree;
tree.child(i).parentpro = splitarr(i);
fprintf('temp tree\n');
disp(tree.child(1));
fprintf('\n');
end
disp(tree);
fprintf("now root tree,tree has %d childs\n",size(tree.child,2));
fprintf('\n');
for i=1:size(data,1)
disp(tree.child(i));
fprintf('\n');
end
fprintf('one iteration ends\n');
end
3、根据某个特征,将数据集分成若干子数据集
function [data,target,splitarr]=splitData(oldData,oldtarget,splitindex)
fn=unique(oldData(splitindex,:));
data=cell(length(fn),1);
target=cell(length(fn),1);
splitarr=zeros(size(fn));
for i=1:length(fn)
fcolumn=find(oldData(splitindex,:)==fn(i));
data(i) =oldData(:,fcolumn);
target(i) = oldtarget(:,fcolumn);
data{i}(splitindex,:)=[];
splitarr(i)=fn(i);
end
end
4、打印决策树
function printTree(tree)
if tree.pro==0
fprintf('(%d)',tree.value);
if tree.parentpro~=-1
fprintf('its parent feature value:%d\n',tree.parentpro);
end
return
end
fprintf('[%d]\n',tree.value);
if tree.parentpro~=-1
fprintf('its parent feature value:%d\n',tree.parentpro);
end
fprintf('its subtree:\n');
childset = tree.child;
for i=1:size(childset,2)
printTree(childset(i));
end
fprintf('\n');
fprintf('its subtree end\n');
end
5、对某个具体的样本进行结果预测
function result=classify(data, tree)
while tree.pro==1
childset=tree.child;
v=tree.value;
for i=1:size(childset,2)
child = childset(i);
if child.parentpro==data(v);
tree=child;
break;
end
end
end
result=tree.value;
end
接下来对数据用代码进行测试
clear all; close all; clc
featurelabels=[1,2,3,4];
trainfeatures=[1,1,1,1,1,2,2,2,2,2,3,3,3,3,3;%each row of trainfeature represent one feature and each column reprensent each examples
0,0,1,1,0,0,0,1,0,0,0,0,1,1,0;
0,0,0,1,0,0,0,1,1,1,1,1,0,0,0;
1,2,2,1,1,1,2,2,3,3,3,2,2,3,1
];
targets=[0,0,1,1,0,0,0,1,1,1,1,1,1,1,0];%represent classification results according to trainfeatures
tree=maketree(featurelabels,trainfeatures,targets,0);
printTree(tree);
data=[2,0,0,1];
result=classify(data,tree);
fprintf('The result is %d\n',result);
关于决策树的原理构建大概就结束了,后期可以继续完成对决策树的剪枝或者将决策树由多叉树转化为二叉树,让决策树更加高效矮小。源码地址:https://github.com/summersunshine1/datamining。
这篇关于决策树的实现原理与matlab代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!