本文主要是介绍【笔记】决策与博弈(上)——Rita_Aloha,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
Ⅰ. 决策与决策树
一、决策
二、决策树
1.决策树
2.决策树模型
3.特征选择
4.决策树的修剪
5.决策树的生成
6.连续属性下的决策树
7.多变量决策树
Ⅰ. 决策与决策树
一、决策
1.(管理学)定义:所谓决策,就是为了实现某一目的而制定行动方案并从若干个可行方案中选择一个满意方案的分析判断过程。
2.一般决策过程包括:
(1)问题识别,即认清事件的全过程,确立问题所在,提出决策目标。
(2)问题诊断,即研究一般原则,分析和拟定各种可能采取的行动方案,预测可能发生的问题并提出对策。
(3)行动选择,即从各种方案中筛选出最优方案,并建立相应的反馈系统。
二、决策树
1.决策树
- 决策树是一类常见的机器学习方法,是一种基本的分类与回归方法,是一种逼近离散值目标函数的方法。
- 决策树学习的目标是根据给定的训练数据集构建一个决策树模型,使它能够对实例进行正确的分类。
- 决策树学习的本质是从训练数据集中归纳出一组分类规则(条件概率模型)。
- 决策树学习的策略是以损失函数为目标函数的最小化;当损失函数确定以后,学习问题就变为在损失函数意义下选择最优决策树的问题。
(定义)分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型:内部结点和叶结点。内部结点表示一个特征或属性,叶结点表示一个类。
2.决策树模型
(1)基本算法
决策树学习的算法是一个递归地选择最优特征并根据该特征对训练数据进行分割、使得对各个子数据集有一个最好的分类的过程。

在决策树的基本算法中,有三种情形会导致递归返回:
- 当前结点包含的样本全属于同一类别,无需划分;-
- 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分;
- 当前结点包含的样本集合为空,不能划分
(2)将决策树看成一个if-then规则的集合(二者互斥且完备)
- 由决策树的根结点到叶结点的每一条路径构建一条规则
- 路径上内部结点的特征对应着规则的条件,而叶结点的类对应着规则的结论
(3)决策树表示给定特征条件下类的条件概率分布
这一条件概率分布定义在特征空间的一个划分上。将特征空间划分为互不相交的单元或区域,并在每个单元定义一个类的概率分布就构成一个条件概率分布。决策树的一条路径对应于划分的一个单元。决策树所表示的条件概率分布由各个单元给定条件下类的条件概率分布组成。
3.特征选择
在信息论与概率统计论中,熵是表示随机变量不确定性的度量。设X是一个取有限个值的离散随机变量,其概率分布为
则随机变量X的熵定义为
由定义可知,熵只依赖于X的分布,而与X的取值无关,所以也可将X的熵记作 H(p) 。熵越大,随机变量的不确定性就越大。
在给定的随机变量X的条件下随机变量Y的条件熵H(Y|X)定义为X给定条件下Y的条件概率分布的熵对X的数学期望
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。一般,熵H(Y)与条件熵H(Y|X)之差称为互信息。
(1)信息增益
①定义:特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵(概率由数据估计所得)与特征A给定条件下D的经验条件熵H(D|A)之差,即
信息增益就表示由于特征A而使得对数据集D的分类的不确定性减少的程度。
②以信息增益为准则的特征选择方法:对训练数据集(或子集)D,计算其每个特征的信息增益,并比较它们的大小,选择信息增益最大的特征。
③信息增益的算法:

(2)增益率/信息增益比
【定义】特征A对训练数据集D的信息增益比定义为其信息增益与训练数据集D关于特征A的值的熵之比,即
其中,,n是特征A取值的个数。
(3)信息增益准则与增益率准则
- 信息增益准则对可取值数目较多的属性有所偏好。
- 增益率准则对可取值数目较少的属性有所偏好。
(4)基尼指数
①基尼系数:
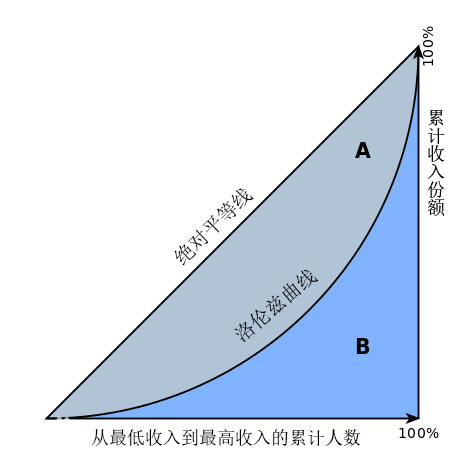
基尼系数(Gini index/Gini Coefficient)是指国际上通用的、用以衡量一个国家或地区居民收入差距的常用指标。基尼系数最大为“1”,最小等于“0”。基尼系数越接近0表明收入分配越是趋向平等。
②定义:分类问题中,假设有K个类,样本点属于第k类的概率为p~k~,则概率分布的基尼指数定义为
③特征A的基尼指数定义:
基尼指数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性。
4.决策树的修剪
(1)预剪枝
①含义:在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树的泛化性能提升,则停止划分并将当前结点标记为叶结点。
②剪枝依据
- 作为叶结点或作为根结点需要含的最少样本个数
- 决策树层数
- 结点的经验熵小于某个阈值才停止
- 每次扩张对系统性能的增益小于某个阈值则停止
③优缺点
- 优点:预剪枝不必生成整棵决策树且算法相对简单,效率很高,适合解决大规模问题。
- 缺点:预剪枝的视野效果问题。有些分支的当前划分虽不能提升泛化性能、甚至可能导致泛化性能暂时下降,但在其基础上进行后续划分却有可能导致性能显著提高。
(2)后剪枝
①含义:先从训练集生成一棵完整的决策树,然后自底向上(PEP是唯一自顶向下剪枝策略)地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能,则将该子树替换为叶结点。从而简化分类模型。
②Cost-Complexity Pruning(CCP)
i.基本思路
- 从原始决策树T~0~开始生成一个子树序列T~0~,T~1~,...,T~K~。其中T~i+1~从T~i~产生,T~K~为根结点。
- 评价子树序列,选择最后被剪枝的最佳决策树T'。
ii.生成树序列
设训练集中包含N个实例,E为分类错误的实例个数,L(T)为树T的叶子结点个数。Breiman等定义了树T的cost-complexity为
,a为参数
若树T的子树S被删除,用叶结点来代替(叶结点所属类用这棵子树中大多数训练实例所属的类代替)生成一棵新树,再用新树分类训练集。设新树比原树T的分类错误个数多M个,而其叶子个数比原来少L(S)-1个,则新树具有同原树T相同的cost-complexity时,
- 树T~0~为最初生成的树;计算树T~i~的每一个非叶子子树,找到具有最小a值的子树;将这一个(或多个)子树用相应的叶结点来代替生成树T~i+1~。如此反复,直至T~K~。
iii.评价,得到T':
- V番交叉验证
- 基于独立剪枝数据集
- 选择的最终数在测试集的分类错误个数不超过 E'+s~e~(E')
设测试集包含N'个实例,用每一个数T~i~对其进行分类测试,E'为其中最小的分类错误个数,对E'的标准错误有如下定义
③Reduced Error Pruning(REP)
i.基本思路
对于决策树T的每一个非叶子子树S,如果子树S被删除,用一叶子结点来代替(叶结点所属类用这棵子树中大多数训练实例所属的类代替)生成一棵新树。如果新树能得到一个较小或相等的对测试集分类错误个数,而且S中不包含具有相同性质的子树,则此子树S被删除,用一叶结点代替。重复此过程,直到任何一子树被叶结点代替而增加其在测试集上的分类错误个数为止。得到最终的树T'。
ii.优点
- 运用REP方法得到是关于测试集原始树的最精确子树,并且是有此精度的规模最小的树。
- REP方法的计算复杂性是线性的,因为决策树中的每个非叶子结点只需要访问一次就可以评估其子树被剪枝的概率。
iii.缺点
- 需要一个单独的测试集。
- 在测试集中不会出现的一些很稀少的实例所对应的原始树的部分,在剪枝过程中将被剪去。一旦测试集比训练集小得多的时候,分类精度将受到极大地限制。
iv.特点:尽管有缺点,REP方法仍被作为一种基准来评价其他剪枝方法的性能。它对于了解两阶段决策树学习方法的优缺点提供了一个很好地初始切入点。
④Pessimistic (Error) Pruning(PEP)
i.特点:PEP是唯一使用自顶向下剪枝策略的事后剪枝方法。为了提高对未来实例的预测可靠性,PEP方法对误差估计增加了连续性校正。
ii.基本思路
设e(t)为结点t处误差,i为覆盖T~t~的叶子,N~t~为子树T~t~的叶子数,n(t)为在结点t处训练实例的数。若
成立,则T~t~应被修剪。其中,
iii.优点
- 比其他的方法速度快。对结点的计算测试从根结点开始,从上到下计算,T的每一棵子树至多被计算测试一次,被删除子树的子树不必再计算。
- 不需要单独的测试集。
iv.缺点
- 树的某个结点的修剪会导致该结点的叶子根据同样准则不需要修剪时仍然会被修剪。
- PEP方法有时会剪枝失败。
⑤Minimum Error Pruning(MEP)
i.基本思路:从树的叶结点开始,向上搜索一棵单一的树以使分类误差的期望概率达到最小。
ii.基本方法
如果训练集类数为k,对于树中的当前非叶子结点t,假设所包含的样本数为N(t),属于主导类i的样本数目为N~i~(t),不属于主导类的样本数为E(t)(E(t)=N(t)-N~i~(t))。结点t中某一样本实例属于类i的期望概率为
其中,P~ki~是第i类的先验概率,m是设置的参数,用来确定先验概率在评估P~i~(t)中的权值。假设所有的结果类是等概率的,即P~ki~=1/k,并且结果类的概率是均匀分布的,即m=k,i=1,2,...,k。则结点t分类误差的期望概率为
- 对于决策树中的叶子结点,利用上式计算决策树中叶结点的误差概率;
- 对于非叶子结点t(假设其子结点是t~1~,...,t~m~),计算该结点t的误差,称之为静态误差STE(t)
- 对于结点t,计算m个分支的误差,并且加权相加,权值为每个分支有用的训练样本的比例,称之为动态(回溯)误差DYE(t)
- 如果STE(T)≤DYE(T),则对结点t的子树进行剪枝
iii.特点
- MEP方法不需要独立的剪枝数据集。
- 在MEP方法中,m的选择非常重要。Cestnik和Bratko建议由专家系统根据不同问题选择m,但在大多数情况下这是不现实的。因此可以利用独立数据集或交叉验证法来选择最佳m值。
⑥Error-Based Pruning(EBP)
- PEP方法的一个改进。此方法中,在访问待剪枝树时是从下至上来访问结点。
- 在剪枝时,它除了删除子树之外,还将此子树嫁接至被删除子树根结点的父结点上。
⑦Rule Post-Pruning(规则后修剪)
i.特点:通过将决策树转化为另外一种数据结构来简化决策树。
ii.步骤
a.从决策树的根结点到叶子结点的每一条路径创建一条规则,将决策树转化为等价的规则集。
-
规则的生成:每条有根到叶的路径对应一条规则,它的前提是这条路径上的所有测试属性的合取,结论是叶结点所属类的判断。
-
对于每一条生成规则,依次判断属性X~i~对实例是否属于结论所属的类的相关程度,如果此相关程度满足某一阈值,则将此属性从这条规则中删除,重复此过程,直到条件不满足为止。
b.对规则集进行评价,这个评价依赖于规则的应用。
- (简单)评价:对于每一条规则,如果省略这条规则的话,剩余的规则在训练集上的分类错误个数不会增加(甚至降低),则将其修剪。重复此过程,直到条件不成立。
c.分类一个实例,找到同其匹配的规则。如果不止一条,应根据某些规则进行处理;如果没有规则同其匹配,默认为训练集中频率最高的类。
iii.优点
- 规则集可以区分决策结点使用的不同上下文。
- 此方法不需要单独的测试集,而且可以通过采用更为复杂的条件删除策略优化此方法。
5.决策树的生成
(1)ID3算法

(2)C4.5算法

(3)CART算法
CART是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。CART假设决策树是二叉树。
①CART生成
决策树的生成就是递归地构建二叉决策树的过程。对回归树用平方误差最小化准则,对分类树用基尼指数最小化准则,进行特征选择,生成二叉树。
i.回归树的生成

ii.分类树的生成

- 算法停止计算的条件是结点中的样本个数小于预定阈值,或样本集的基尼指数小于预定阈值(样本基本属于同一类),或者没有更多特征。
②CART剪枝
i.基本思路
- 从生成算法生成的决策树T~0~底端开始不断剪枝,直到T~0~的根结点,形成一个子树序列{T~0~,T~1~,...,T~n~};
- 通过交叉验证法在独立的验证数据集上对子树序列进行测试,从中选择最优子树。
ii.算法

iii.说明
- Breiman等人证明:可以用递归的方法对树进行剪枝。将α从小增大,0=α~0~<α~1~<...<α~n~<+∞,产生一系列区间[α~i~,α~i+1~),i=0,1,...,n;剪枝得到的子树序列对应着区间α∈[α~i~,α~i+1~),i=0,1,...,n的最优子树序列{T~0~,T~1~,...,T~n~},序列中的子树是嵌套的。
- 对T~0~中每一内部结点t,
计算 他表示剪枝后整体损失函数减少的程度。在T~0~中剪去g(t)最小的T~t~,将得到的子树作为T~1~,同时将最小的g(t)设为α~1~。T~1~为区间[α~1~,α~2~)的最优子树。如此剪枝下去,直至得到根节点。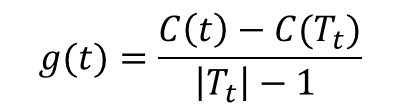
- 利用独立的验证数据集,测试子树序列T~0~,T~1~,...,T~n~中各棵子树的平方误差或基尼指数。平方误差或基尼指数最小的决策树被认为是最优的决策树。在子树序列中,每棵子树T~1~,T~2~,...,T~n~都对应于一个参数α~1~,α~2~,...,α~n~。所以,当最优子树T~k~确定时,对应的α~k~也确定了,即得到最优决策树T~α~。
6.连续属性下的决策树
(1)连续值处理
① 基本思路:利用连续属性离散化技术对结点进行划分。
② 算法举例
【采用取值区间二分离散化的方法来处理连续属性】
i.找出训练样本在该连续属性上的最大和最小值,在最大和最小值限定的取值区间上设置多个等分断点;
ii.分别计算以这些断点为分列点的信息增益值,并比较;
iii.具有最大信息增益的断点即最佳分裂点,自该分裂点把整个取值区间划分为两部分,相应的依据记录在该属性上的取值,也将记录集划分为两部分。
(2)缺失值处理
① 抛弃缺失值:
- 若属性缺失值较多或是关键属性值缺失 , 创建的决策树将是不完全的 , 此时一般不采用抛弃缺失值。
- 数据库具有极少量的缺失值且缺失值不是关键属性值 , 为加快创建决策树的速度 , 采用抛弃属性缺失值的方式创建决策树 。
② 补充缺失值
补充算法规则一:如果存在创建决策树时,某个子节点包含的所有样本都属于同一个类,则首先将该节点中的所有缺失值补充为分支属性值,同时将该样本包含在该分支中,取消在其它的分支的可能分配。如果规则一在创建决策树时会造成较大的改动或生成的决策树产生的规则给用户的知识偏差太大 , 则采用规则二 。
补充算法规则二:以与缺失值样本具有最大相似度的确定值样本的属性值作为对缺失值样本的修改,同时取消决策树中其他分支的可能分配。一直到将所有缺失值补充完整。
- 缺失值较少时按照补充规则是可行的。但如果数据库的数据较大、缺失值较多,填充后的数据库创建的决策树可能和根据正确值创建的决策树有很大变化 。
③ 概率化缺失值
对缺失值的样本赋予该属性所有属性值的概率分布,即将缺失值按照其所在属性已知值的相对概率分布来创建决策树 。用系数F进行合理的修正计算的信息量,F表示所给属性具有已知值样本的概率:
![]()
7.多变量决策树
(1)多变量决策树的特点
目前大多数决策树算法都是单变量决策树,即在每个节点处只对单个属性进行检验,这一限制使得子树重复和有些属性在树中的某条路径上被多次检验。为了克服这一限制,人们提出了多变量归纳学习方法,即在树的节点上可以同时检验多个属性,这种系统能够产生新的相关属性。
(2)构造多变量决策树的启发式函数的关键问题
- 要充分考虑属性之间的关联性,并以此为依据选择合适的属性组合作为节点;
- 在降低树的复杂性的同时,还要保证生成规则的可读性。
(3)构造多变量决策树的基本思路
① 根据粗糙集理论中的属性依赖度找出依赖度最大的一个条件属性作为该节点的第一个属性,记为A~f~,它为决策属性提供最多的确定性信息;
② 再用信息系统中条件属性集的离散度的概念,找出与A~f~的合取构成的新的属性的离散度最小的一个条件属性作为该节点的第二属性,记为A~s~;
③ 将A~f~与A~s~的合取式A~f~∧A~s~作为内节点的检验标准。
整理自:
1.http://courseware.eduwest.com/courseware/0469/content/content/neirong/0601.htm
2.车文博 主编.《心理咨询大百科全书》.杭州:浙江科学技术出版社.2001.第519页.
3.周志华 著. 《机器学习》. 清华大学出版社.2016.
4.李航 著. 《统计学习方法》. 清华大学出版社.2012.
5.谢妞妞. 《决策树算法综述》. 软件导刊. 2015.11
6.https://baike.baidu.com/item/%E5%9F%BA%E5%B0%BC%E7%B3%BB%E6%95%B0/88365?fromtitle=%E5%9F%BA%E5%B0%BC%E6%8C%87%E6%95%B0&fromid=360504&fr=aladdin
7.https://www.cnblogs.com/luban/p/9412339.html
8.王熙照 游自英.《决策树简化(剪切)方法综述》. 计算机工程与应用. 2004.27
9.王黎明 刘华.《决策树中避免过度拟合的方法》. 软件导刊. 2006.
10.魏红宁.《决策树剪枝方法的比较》. 西南交通大学学报. 2005.
11.陈广花 王正群 刘风 俞振州.《一种多变量决策树的构造与研究》. 计算机工程与应用. 2010.
12.许俊.《决策树算法中的连续属性处理方法》. 河北理工学院学报. 2007.
13.巩固 张虹.《决策树算法中属性缺失值的研究》. 计算机应用与软件. 2008.
14.张维迎 著.《博弈论与信息经济学》. 格致出版社. 2004.
15.吴广谋 吕周洋 编著.《博弈论基础与应用》. 东南大学出版社. 2009.
16.[以]迈克尔·马希勒 / [以]埃隆·索兰 / [以]什穆埃尔·扎米尔 著;赵世勇 译.《博弈论》. 格致出版社. 2018.
17.鲁斌 刘丽 李继荣 姜丽梅 编著.《人工智能及应用》. 清华大学出版社. 2017.
这篇关于【笔记】决策与博弈(上)——Rita_Aloha的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







