抽样偏差（Sampling Bias）与 分层抽样（Stratified Sampling）

个人觉得， 把分层抽样称为“分类采样”会更贴切一些。通常最基本的采样手段是：随机抽样，但是在很多场景下，随机抽样是有问题的。最简单也最有说服力的例子就是身高和体重在性别上的差异，在对它们进行抽样时必须考虑性别因素。我们可以粗略地说：女性的身高符合165为中心的正态分布，体重符合50公斤为中心的正态分布，而男性身高则可能是175为中心的正态分布，体重是60公斤中心的正态分布。还有一些示例未必那么明细，需要一定的统计数据支持和业务知识来发现。例如：如果现在要发起一个啤酒品牌知名度的调查问卷，我们能使用随机抽样来筛选参与调查的候选人吗？答案是否定的，因为性别在这个调研的目标人群中发挥着显著的影响，不能进行随机抽样，否则抽样数据将“严重失真”，并不能反映真实的数据分布，此时应该性别进行分层抽样，增大男性在抽样中的比例。

当数据的“某些特征”对数据分布有显著影响时，就应考虑是否要将这些特征纳入到分层抽样的范围中了。在《Hadnson ML》一书第二章中提到这样一个案例：一个非常直白的认知是：一个地区的收入中值与该地区的房价是有密切关系的。在提取训练数据集时，如果采用随机抽样，就抹掉了收入水平在房屋价格中发挥的显著作用，这种随机抽取的样本已经发生了“失真”，则预测结果就很难精准了。所以，作者提出：应该按收入水平进行分层采样。

进行分层采样的前提是目标属性往往是类别化的离散值，对于那些连续的数值型属性，通常需要进行一下“预处理”：把连续的数值型数据转换为离散的类别型数据。在Pandas的DataFrame中，有一个方法cut：https://pandas.pydata.org/docs/reference/api/pandas.cut.html#pandas.cut 就是专门负责这种处理的。请看如下的示例：

import pandas as pd
import numpy as np
info_nums = pd.DataFrame({'num': np.random.randint(1, 100, 5)})
print(info_nums)
info_nums['num_bins'] = pd.cut(x=info_nums['num'], bins=[1, 50, 100])
print('---------------')
print(info_nums)
print('---------------')
info_nums['num_bins'] = pd.cut(x=info_nums['num'], bins=[1, 50, 100], labels=['Lows', 'Highs'])
print(info_nums)

输出结果如下：

   num
0   79
1    9
2   71
3   90
4   24
---------------num   num_bins
0   79  (50, 100]
1    9    (1, 50]
2   71  (50, 100]
3   90  (50, 100]
4   24    (1, 50]
---------------num num_bins
0   79    Highs
1    9     Lows
2   71    Highs
3   90    Highs
4   24     Lows

从测试代码可知:

• bins给出连续的数组区间，落在区间内的值被归为一类，例如：bins=[1, 50, 100]意味：1-50是一个区间，50-100是一个区间，79会落在(50, 100]的区间上，9会落到(1, 50]的区间上
• labels会针对每一个区间起一个别名，例如：labels=['Lows', 'Highs']意味：(1, 50]的区间将被称为Lows，(50, 100]的区间将被称为Highs。使用了labels之后，落地的值就将变成注的离散值了。

接下来我们看一下《Hadnson ML》一书中的例子：

housing["income_cat"] = pd.cut(housing["median_income"],bins=[0., 1.5, 3.0, 4.5, 6., np.inf],labels=[1, 2, 3, 4, 5])

参考前面的例子可知：(0, 1.5]区间内的值将被标记为1, (1.5, 3.0]区间内的值将被标记为2，依次类推。

获得收入“收入等级”分类列之后，我们会可以依据离散的收入分类进行分层抽样了。对此，Scikit-Learn也提供了现成的函数：

from sklearn.model_selection import StratifiedShuffleSplitsplit = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
# 不同于train_test_split，StratifiedShuffleSplit在切分时还需要指定分类列，算法会参考
# 每一个分类在总体中所占的比列（份额）来对数据进行抽样，以避免抽样过程中出现“失真”
for train_index, test_index in split.split(housing, housing["income_cat"]):strat_train_set = housing.loc[train_index]strat_test_set = housing.loc[test_index]

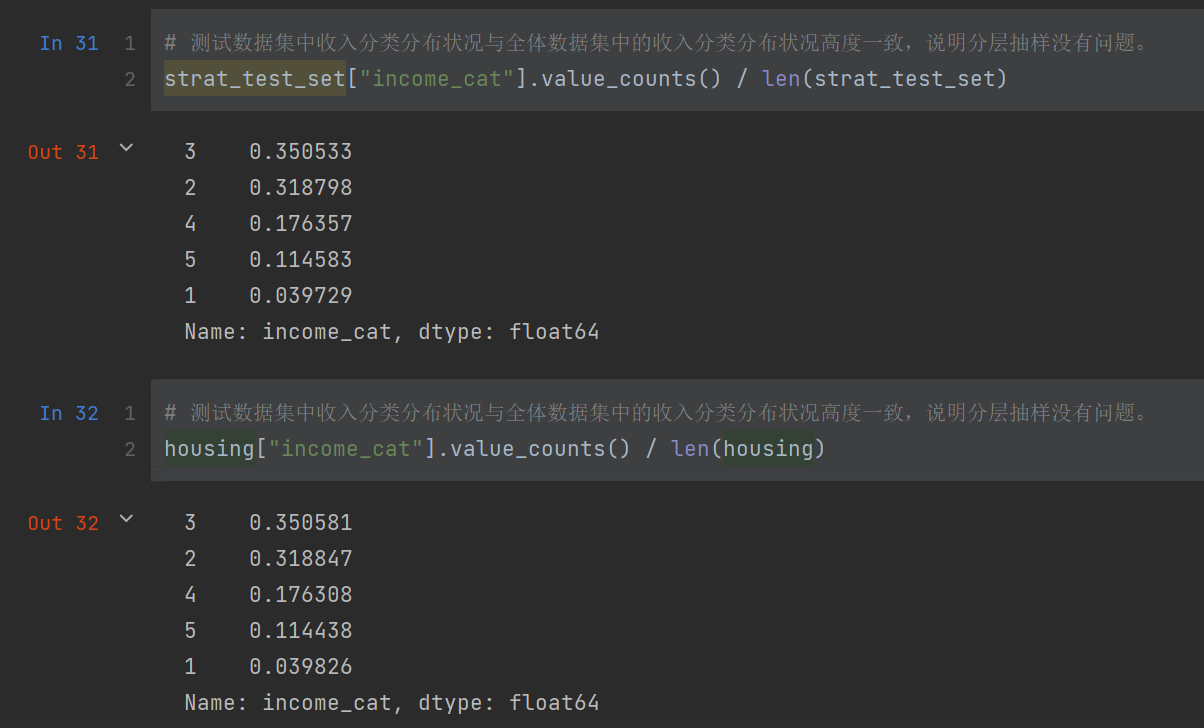
完成抽样后，我们可以分别检测一下测试数据集与全体数据集中收入分类的分布状况，如果它们保持一致的比重，则说明分层抽样没有问题：