本文主要是介绍SMD-Nets: Stereo Mixture Density Networks,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
paper | project
Abstract
尽管在过去的几年中,深度学习大大提高了立体匹配的精度,但有效地恢复尖锐边界和高分辨率输出仍然具有挑战性。在本文中,我们提出了立体混合密度网络(Stereo Mixture Density Networks, SMD-Nets),这是一种简单而有效的学习框架,可与广泛的2D和3D体系结构兼容,改善了这两个问题。
具体来说,我们利用双峰混合密度作为输出表示,并表明这允许在不连续点附近进行清晰而精确的视差估计,同时明确地对观测中固有的任意不确定性进行建模。此外,我们将视差估计作为图像域的连续问题,允许我们的模型在任意空间精度查询视差。
我们在一个新的高分辨率和高度逼真的合成立体数据集上进行了综合实验,包括8Mpx分辨率的立体 图像对,以及在真实世界的立体数据集上。我们的实验证明了在目标边界附近的深度精度和在标准gpu上超高分辨率视差图的预测。

Motivation
目前仍有两个主要问题未得到解决:预测准确的深度边界和在有限的内存和计算量下生成高分辨率输出。
第一个问题由于神经网络是平滑函数逼近器,它们常常无法很好地重建对象边界,导致“bleeding””伪影转换为点云。这些伪影可能不利于随后的应用,如3D重建或3D对象检测。因此,虽然被最常用的视差度量忽略,但轮廓的准确 3D 重建是任何立体匹配算法的理想特性。
标准的立体网络在每个像素直接回归一个标量视差。这种输出表示受到过平滑的影响,并且没有暴露潜在的任意不确定性。后一个问题可以通过使用参数分布(如高斯分布或拉普拉斯分布)对视差进行建模来解决,但过度平滑问题(over-smoothing issue)仍未解决。我们工作的一个关键结果是证明用双峰输出表示替换单峰输出表示足以显著缓解这个问题。
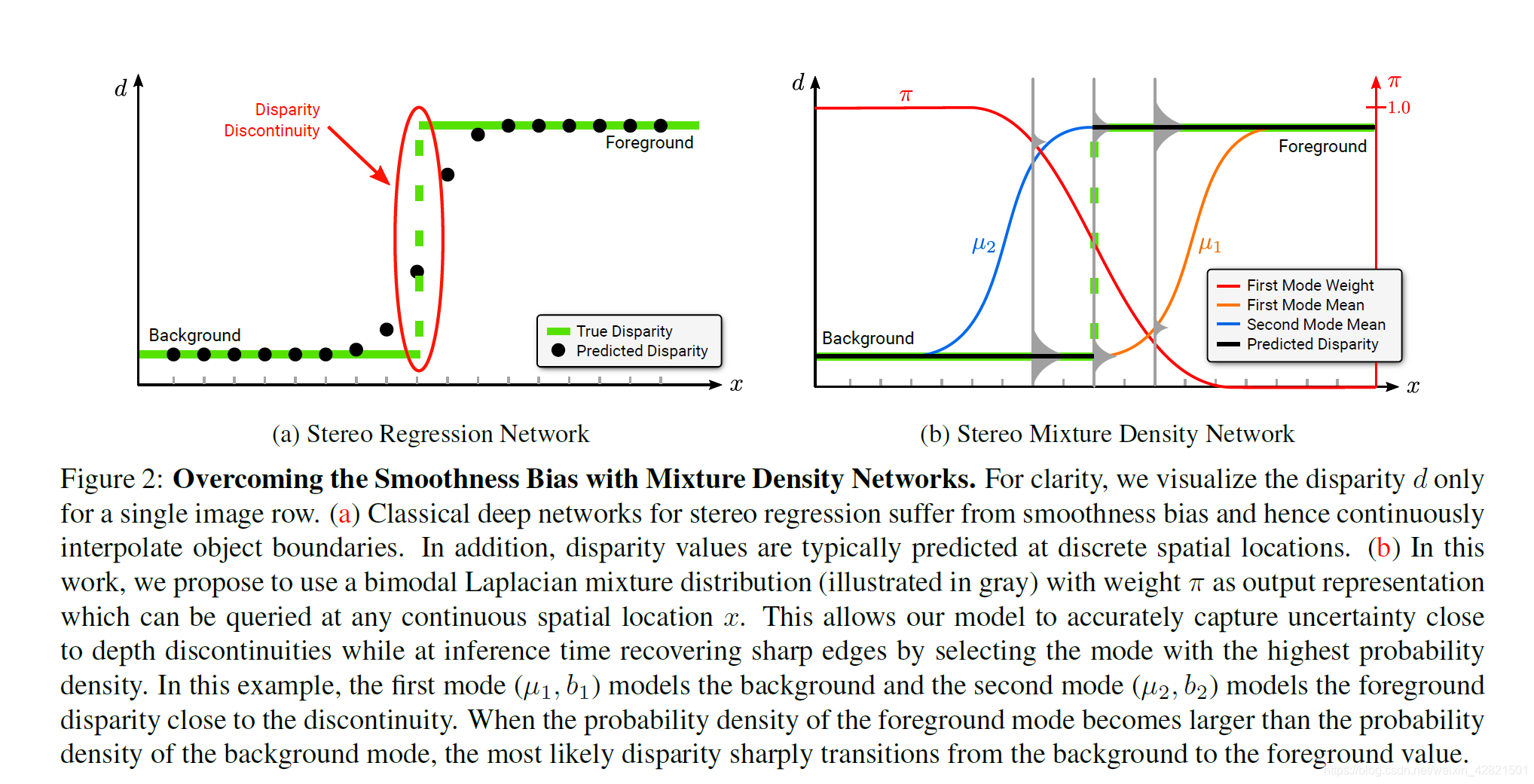
标准的立体网络在每个像素直接回归一个标量视差。这种输出表示受到过平滑的影响,并且没有暴露潜在的任意不确定性。后一个问题可以通过使用参数分布(如高斯分布或拉普拉斯分布)对视差进行建模来解决,但过度平滑问题(over-smoothing issue)仍未解决。我们工作的一个关键结果是证明用双峰输出表示替换单峰输出表示足以显著缓解这个问题。
另一种方法估计一组离散视差值上的非参数分布。然而,当估计的分布是多模态(multi-modal)时,这种方法会导致不准确的结果。一些研究通过在训练过程中实施单峰约束(unimodal constraint)来解决这个问题。相反,我们通过采用一个简单而有效的双峰表示来显式地建模对象边界处分布的双峰性质(bimodal nature)。在并行工作中,还可以在一组深度值上启发式设计的多模态基态真值的监督下预测多模态分布。与之相反,我们的双峰方法可以通过最大化可能性来学习,而不需要对分布本身进行直接监督。
此外,现有的方法仅限于在固定分辨率的图像网格的像素位置的离散预测,而几何是一个分段连续的数量,对象的边界可能不与像素中心对齐。
通过增加额外的上采样层来提高输出分辨率部分地解决了这个问题,因为这会导致内存和计算量的显著增加。
Core idea
在这项工作中,我们解决了这两个问题。我们的主要贡献是学习一种在对象边界和比例上精确到高输出分辨率的表示。特别地,我们将该任务定义为一个连续估计问题,并利用双峰混合密度作为输出表示。并且稳文中的方法可以与几乎任何stereo主干有利地结合。
我们的简单公式可以让我们(1)避免深度不连续处的出血现象,(2)在具有恒定内存的任意空间分辨率下回归视差值,(3)提供了一种测量任意不确定性的方法。
实施方法
我们首先使用卷积骨干(左)将立体对编码为特征图。
接下来,我们通过多层感知器head估计任意连续2D位置的混合密度分布的参数,以双线性插值特征向量作为输入(中间)。由此,我们得到了视差和不确定性图uncertainty map(右)。
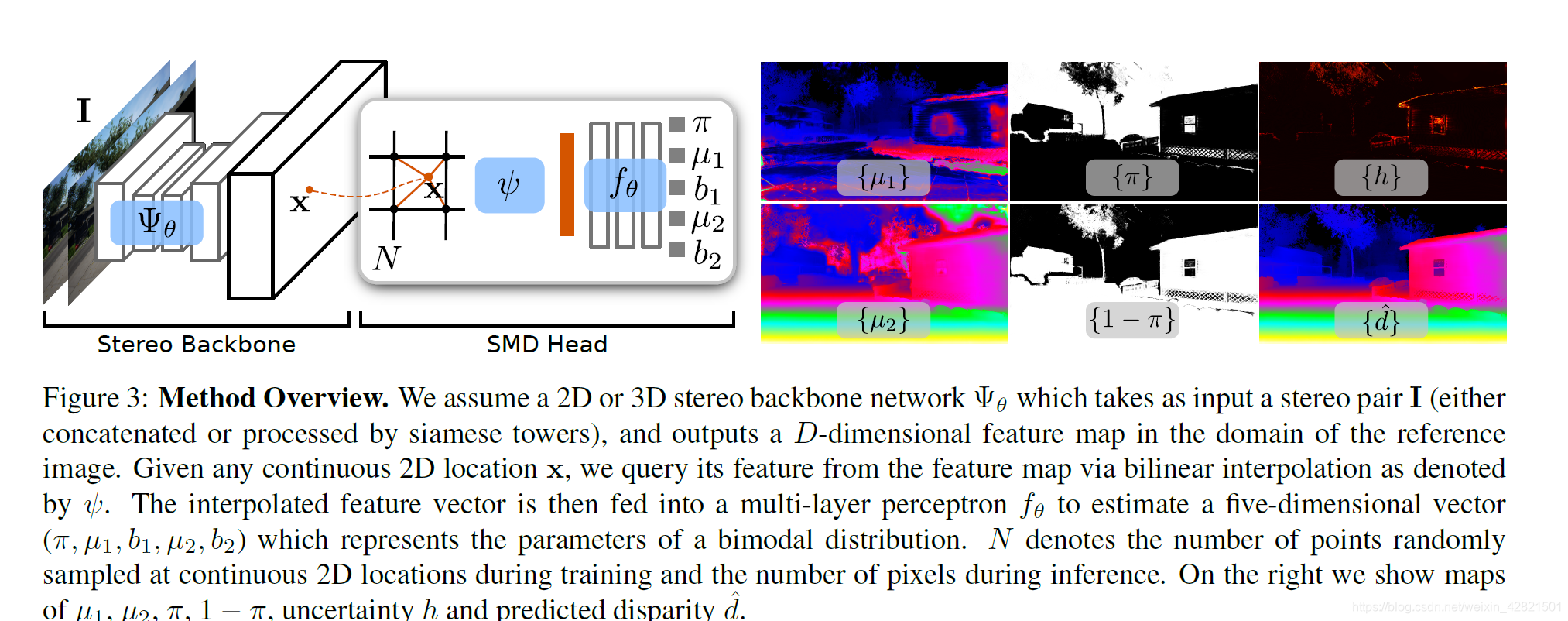
Problem Statement
由于神经网络的平滑偏差,经典的立体回归网络存在过平滑问题。在这项工作中,我们利用混合分布作为输出表示来克服这一限制。
更具体地说,我们使用具有权重的双峰拉普拉斯算子
和两种模式的混合分布对连续概率分布进行建模在特定像素上的差异。
使用两种模式的混合分布允许我们的模型捕获前景以及物体边界处的背景视差。
在inference中,我们通过选择恢复清晰的对象边界密度值最高的模式。因此,我们的模型能够以一种不连续的方式从一种视差过渡到另一种,同时只依靠相关函数的回归,它们是相对于图像域是平滑的,因此可以很容易地用神经网络来表示。
Stereo Mixture Density Networks
骨干网络表示如下:
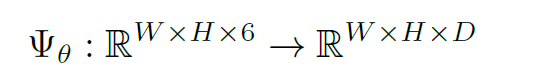

这种网络的例子是标准的 2D 卷积
网络,或执行 3D 卷积的网络。
对于 2D 网络,可以concatenate立体图像对
作为输入或通过共享权重的双分支处理,就像通常为 3D 架构所做的那样。 相似地,这种通用公式也适用于结构化轻量设置(例如,Kinect 设置,输入WH,单目深度估计问题输入WH*3)。
由于几何是一个分段连续量,我们应用确定性变换来获得 WH 中任何连续位置的特征点。 更具体地说,对**于每个连续的 2D 位置 ,我们从特征图WH*D 中四个最近的像素位置对特征进行双线性插值**(上采样能写的这么diao?)。 更正式地,我们将这种转换描述为:
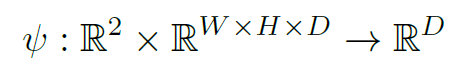
最后,我们使用多层感知器将这个抽象特征表示映射到一个五维向量 ,它表示单变量双峰混合分布的参数:
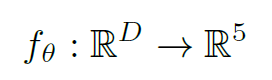
请注意,我们重新使用了参数符号来简化符号。 在下文中,我们将 f 称为 SMD head。为了对可以表达接近视差不连续性的两种模式的视差分布进行稳健的建模,我们选择双峰拉普拉斯混合作为输出表示:
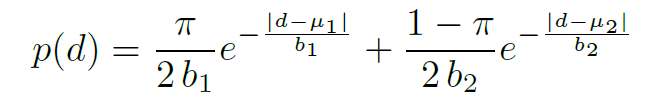
总之,我们的模型可以简洁地表示为:
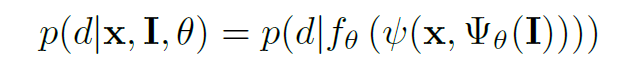
在inference时,我们通过选择密度值最高的模式来确定最终的视差d:

请注意,我们的公式允许查询视差d在任何连续的 2D 像素位置,可实现具有清晰描绘的对象边界的超高分辨率预测。 如下图所示:
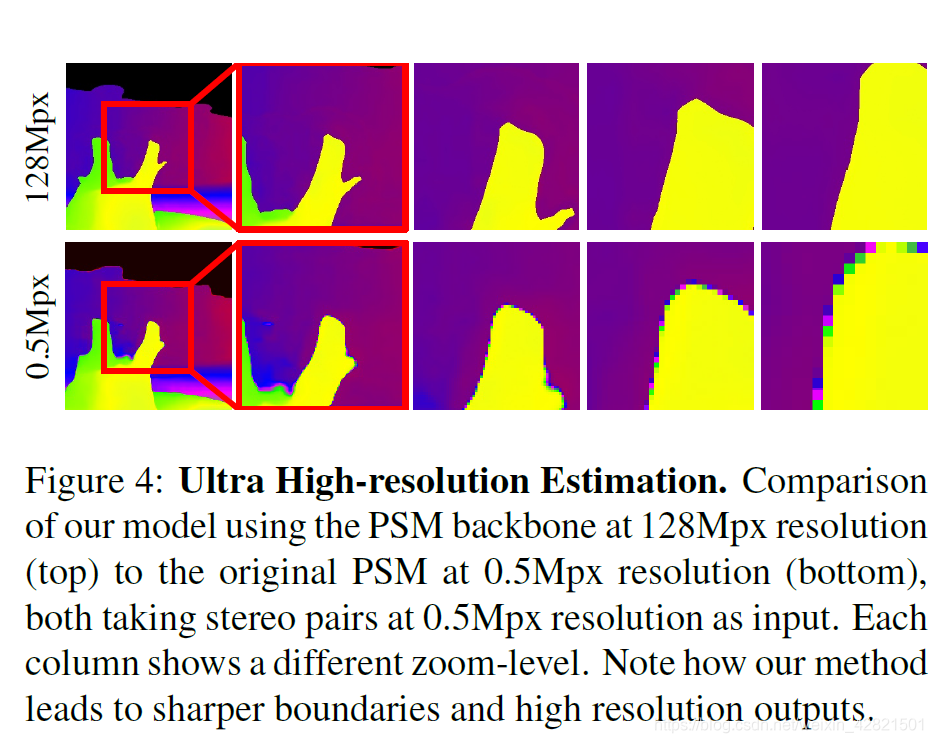
我们的模型还允许通过评估连续混合分布的微分熵来捕获预测视差的任意不确定性:
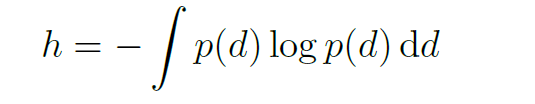
在实际应用中,我们使用数值求积的方法来求得积分的近似.
Loss Function
我们考虑监督设置,通过最小化负对数似然损失来训练我们的模型:

Sampling Strategy
虽然朴素的策略从图像域ω随机均匀地采样像素位置,但我们的框架也允许利用定制的采样策略来关注训练期间的深度不连续性。在训练过程中,我们采用了深度不连续感知(DDA)采样方法,该方法明确支持位于对象边界附近的点,同时保持整个图像空间的均匀覆盖。更具体地说,给定一个往返调度原则的训练时间,
我们首先计算一个对象边界掩码,在这个掩码中,如果它的(4-连通)邻居的差异超过1,它就被认为是边界的一部分。然后使用ρ×ρ核来扩大该掩模的边界区域。
我们在实验部分报告了使用不同ρ值的分析。给定训练点的总数,我们从属于深度不连续区域的所有像素的域中随机均匀地选择n/2个点,并从所有剩余像素的连续域中均匀地选择n/2个点。在推断时,我们利用我们的模型来预测(任意分辨率)网格每个位置的视差值。
Stereo Super-Resolution
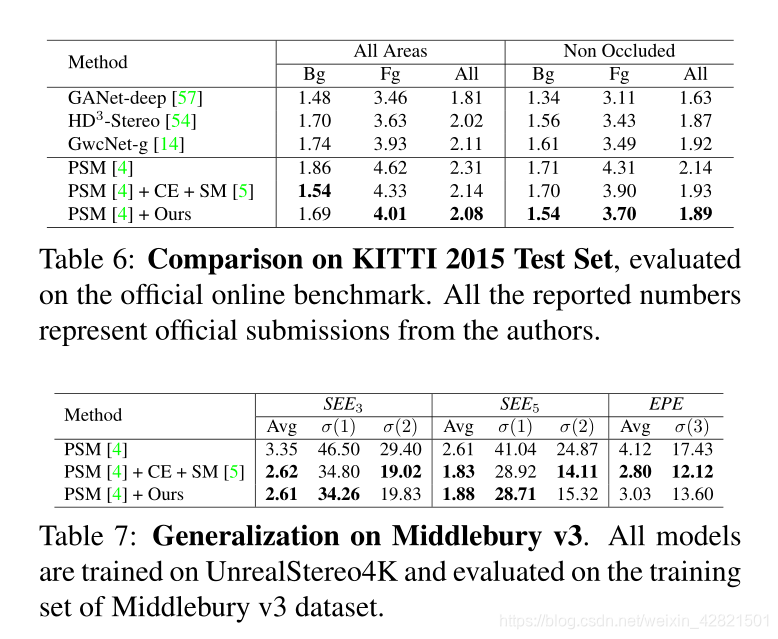
我们的连续配方使我们能够以比input更高的分辨率生成griund truth,我们称之为立体声超分辨率。相比之下,经典的立体方法不能在不改变其结构的情况下实现任意的超分辨率.
这篇关于SMD-Nets: Stereo Mixture Density Networks的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








