空间计量 | 空间OLS回归

本文主要是介绍空间计量 | 空间OLS回归，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

通常情况下，我们研究X对于Y的影响作用关系，可以使用OLS回归，并且OLS回归时默认认为数据之间具有独立性（即行与行之间具有完整的独立性并不互相影响），但当前有的数据并非如此，比如各省GDP之间具有影响作用关系，北京的GDP可以拉动天津的GDP提升，即如果研究的样本是31个省，那么此31个省（样本）之间本身就具有相互影响关系，即样本之间不独立，而且样本之间具有‘空间性’，此则空间计量研究的内容，空间计量是在普通计量基础上加入‘空间性’，此‘空间性’是通过‘空间权重矩阵’进行体现，其表示样本之间的相关关系情况，比如31个省市之间是否具有相邻关系，也或者31个省市之间的物理距离或者经济距离情况等。‘空间权重矩阵’类似如下图：

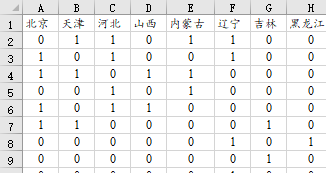
比如上图中的空间权重矩阵，其表示中国31个省市之间空间关系，此关系为两两省份之间是否具有相邻性，数字1表示具有相邻关系数字0表示没有。比如北京和天津相邻因而为1，也比如上海和浙江相邻为1。当然里面的数字也可以为小数，小数时很可能就是表示两两间的比如物理距离或者经济距离等。但无论如何，空间权重矩阵具有如下特点：

• 第1：对称性； 其一定满足M(i, j)=M(j, i)这一特点，该特点很明显，北京和天津相邻，那么天津和北京也相邻；

• 第2：主对角线为0；主对角线表示自己与自己的关系，永远为数字0；

• 第3：n*n阶矩阵，比如31个省那就是31*31矩阵，只是第1行为省的名称而已；

• 第4：标准化处理；试着想象下，数字如果是物理距离，那么北京挨着天津很近所以数字很小，但是北京离新疆或者海南就会非常远数字很大，因而通常需要对空间权重矩阵进行量纲化处理，正常情况下会使用‘按行标准化’处理这一方式，其表示某行的任意数字除以该行数字之和，处理后其数字的实际意义为相对在空间上的相对距离值。

本文档的空间OLS回归，其实质就是OLS回归，但其会输出模型LM检验等，用于进一步判断适合的空间模型使用。

在使用空间计量相关的方法时，其均需要‘空间权重矩阵’和‘分析数据’两份数据，并且均需要单独上传到SPSSAU中，并且对‘分析数据’进行分析时，下拉选择对应的‘空间权重矩阵’，操作上分为以下3个步骤。

• 第1：上传‘空间权重矩阵’文档

  此处需要注意：上传的数据需要为n*n阶格式，而且第1行为空间点的名称（比如31省市的名称）。类似下图格式：

  

• 第2：上传‘分析数据’文档

  此处需要注意：比如31省市数据，‘空间权重矩阵’有着该31个空间点的顺序比如北京-》天津-》河北-》山西-》…，那么‘分析数据’的31行数据也需要按此顺序才可以。

• 第3：针对‘分析数据’进行分析，并且选择‘空间权重矩阵’文档

  此处需要注意：进行某空间研究方法时需要下拉选择‘空间权重矩阵’，选择后，SPSSAU会自动判断其是否为‘空间权重矩阵’格式，包括是否为n*n阶结构，是否具有对称性等。如果不是则会进行信息提示，请勿必注意空间权重矩阵数据格式。

空间OLS回归案例

• 1、背景

  当前有一份空间数据，其为美国哥伦布市49个社区的相关数据，包括犯罪率（crime）、房价（hoval）和家庭收入（income），当前希望研究房价和家庭收入对于犯罪率的影响关系，并且在研究这一影响关系时，考虑空间性。部分数据如下图所示：

  

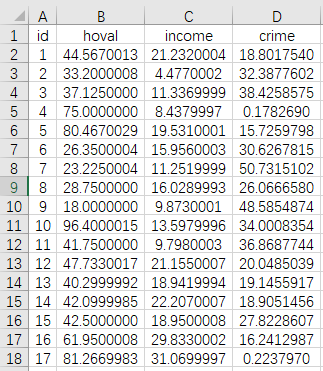
  上面展示的是‘分析数据’，共有49个社区，该49个社区对应的‘空间权重矩阵’如下图所示：

  

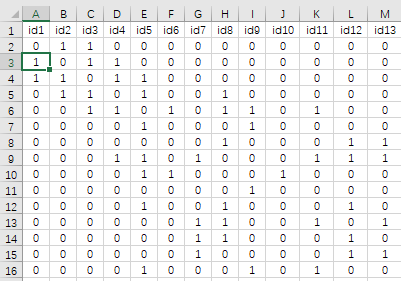
  图中数字1表示两个空间点（社区）之间相邻，数字0表示两个社区不相邻。空间权重矩阵数据可点击此处下载。

• 2、理论

  空间OLS回归的目的是进行OLS回归时计算LM检验，利用LM检验进一步判断适合的空间计量模型，其会输出LM检验用于判断选择最优的空间计量模型，其回归结果实质上就是普通OLS回归模型结果。

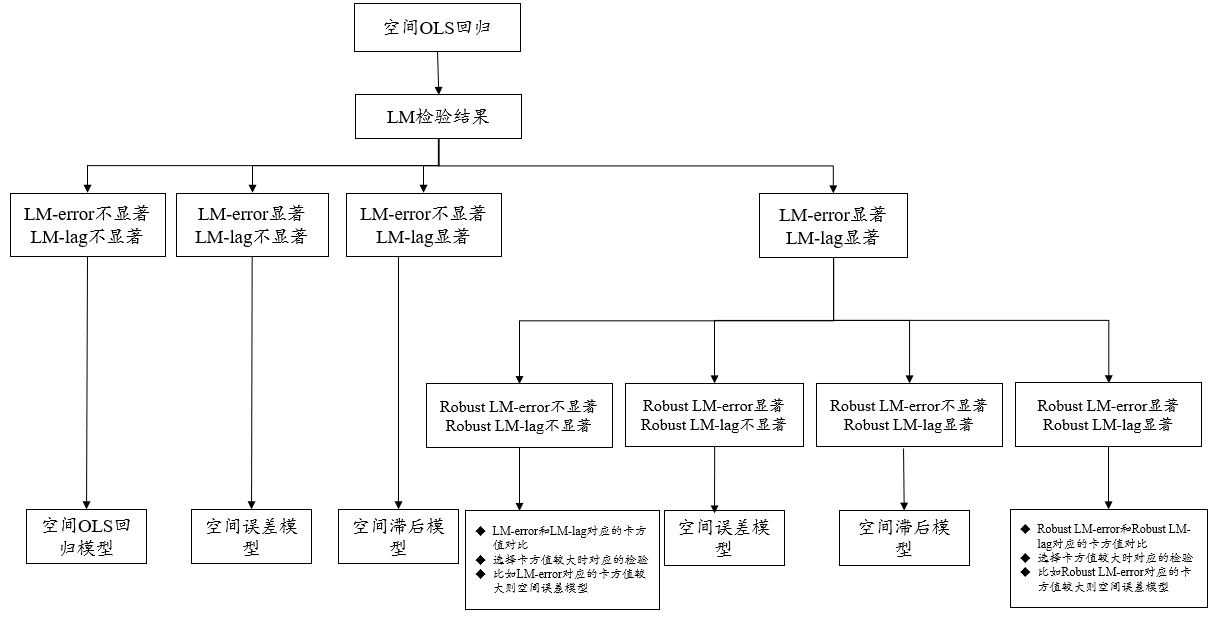
  LM检验是空间OLS回归最核心表格，结合LM检验结果，可选择最优的空间计量模型，比如是使用空间滞后SLM(也称SAR模型)，还是空间误差模型，也或者应该不考虑空间性直接使用OLS回归结果等，针对LM检验的判断流程建议如下图所示：

  

  • 进行空间OLS回归时输出4个LM检验，首先针对LM-error和LM-lag进行分析，如果二者均不显著，则应该使用OLS回归即可，如果仅LM-error显著则使用空间误差模型，如果仅LM-lag显著则使用空间滞后模型，如果二者均显著，则需要进一步查看Robust LM检验；

  • 基于LM-error和LM-lag均显著时，则需要结合Robust LM-error和Robust LM-lag检验进一步判断，如果Robust LM-error和Robust LM-lag检验均不显著，此时退回到上一步即对比LM-error和Lm-lag这两个检验对应的卡方值，哪个更大则使用更大对应的模型，比如LM-error检验的卡方值更大则使用空间误差模型，如果LM-lag检验的卡方值更大则使用空间滞后模型；如果仅Robust LM-error显著则使用空间误差模型，如果仅Robust LM-lag显著则使用空间滞后模型，如果Robust LM-error和Robust LM-lag检验二者均显著，此时可使用二者中对应卡方值更大时对应的模型（或者结合信息准则判断模型优劣），比如Robust LM-lag检验的卡方值比Robust LM-error检验时的卡方值更大，那么可使用空间滞后模型，当然也可考虑使用空间滞后误差模型（即一般空间模型SAC)。

  • 除此之外，通常情况下，空间OLS回归（即普通OLS回归）可作为一个参照模型与最终使用的空间模型进行对比分析。

• 3、操作

  本例子操作如下：

  

  下拉选择‘空间权重矩阵’文档即spatialweight这份数据，默认对空间权重矩阵行标准化处理，需要注意的是，空间权重矩阵通常需要进行行标准化处理。

• 4、SPSSAU输出结果

  SPSSAU共输出7个表格，分别是模型基本参数等、空间OLS模型分析结果、空间OLS模型LM检验汇总、空间OLS模型相关检验汇总、信息准则指标结果、空间效应分析和空间OLS回归分析结果-简化格式表格，如下所述。

  表格	说明
  模型基本参数等	输出模型的基础参数值信息等
  空间OLS模型分析结果	输出空间OLS（实质上就是OLS回归结果）
  空间OLS模型LM检验汇总	输出核心的LM检验结果，用于判断选择最优的空间计量模型
  空间OLS模型相关检验汇总	输出比如异方差检验结果等
  信息准则指标结果	输出ML极大似然法估计的信息准则指标等
  空间效应分析	输出空间效应分析表格
  空间OLS回归分析结果-简化格式表格	输出OLS回归结果的简化表格格式

• 5、文字分析

  

  上表格模型的基本参数信息，包括具体的空间计量模型名称，是否使用稳健标准误差，空间权重矩阵名称及是否对其进行标准化处理等，模型估计方法等，表格中仅展示模型的参数信息等无特别分析意义。

  

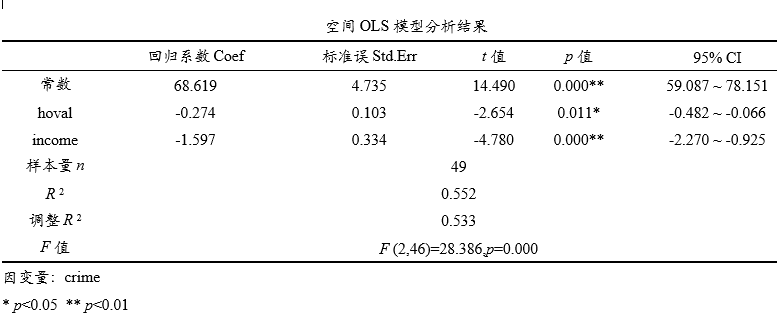
  上表格展示OLS模型回归结果，但空间OLS回归核心目的在于得到LM检验，用于判断最终应该使用哪个空间模型，结合LM检验流程图最终可进行判断选择，当然最终也可能使用OLS回归结果（此种情况下意味着没有空间效应），如果是此类情况则直接使用上表格即可。

  

  上表格展示最核心的LM检验结果，从上表格可以看到，LM-error和LM-lag这两个检验均呈现出显著性，因而进一步对Robust LM-error和Robust LM-lag这两个进行分析，但是这两项均没有呈现出显著性，因而又退回去判断LM-error和Lm-lag检验。LM-error对应的卡方值为4.246 < Lm-lag检验对应的卡方值6.595，因而最终使用LM-lag检验对应的空间滞后模型（即SLM模型或者SAR模型）结果较优，那么后面则需要使用SPSSAU对应的空间滞后模型进行分析。

  

  上表格展示OLS回归对应的异方差White检验，BP检验和JB检验等，由于空间模型更多关注于空间性，因而上表格的关注度通常不高，当然如果有着异方差问题时，此时可使用稳健标准误差法进行估计即可。

  

  上表格展示信息准则结果表格，包括llf值和另外两个值即AIC值和Schwarz准则值，llf值通常越大越好，但是AIC值和Schwarz准则值均是越小越好，如果希望对比模型优劣，可考虑使用上述三个指标，但需要注意的是，极大似然法估计ML法时才会输出上述指标，如果是比如GMM估计则没有输出上述指标。

  

  空间计量研究时，通常会关注于空间效应，其中直接效应ADI反映自变量X对于自身区域Y的平均影响效应情况，间接（溢出）效应AII反应自变量X对其它区域Y的平均影响效应情况，总效应ATI=直接效应ADI+间接（溢出）效应AII。但是本文档中为空间OLS回归，其就是普通OLS回归，并没有任何的空间效应，因而AII值全部均为0。

  

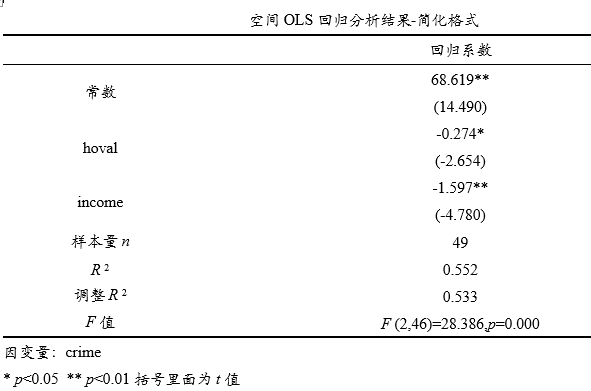
  上表格展示OLS回归的简化表格格式，由于本案例数据最终应该使用空间滞后SLM（或SAR模型），因而本处不单独进行分析。

• 6、剖析

  • 涉及以下几个关键点，分别如下：

  • 空间OLS回归时需要核心关注LM检验，结合LM检验流程选择最优的空间计量模型，LM检验的解读上带有一定的主观性判断，建议结合实际数据情况进行选择使用。

  • 空间OLS回归，其实质上就是普通OLS回归，但其加入空间权重矩阵因而会输出LM检验结果。

疑难解惑

• 空间计量LM检验的解读？

• 通常情况下，LM检验时首先针对LM-error和LM-lag进行判断，如果二者均显著则应该进一步使用Robust LM-error和Robust LM-lag进行判断选择，如果仅LM-error显著则使用空间误差模型，如果仅LM-lag显著则使用空间滞后模型，如果二者均不显著则使用空间OLS回归即此时没有空间效应

• 如果LM-error和LM-lag均显著时，进一步对Robust LM-error和Robust LM-lag进行判断，如果Robust LM-error和Robust LM-lag均显著，则通常可选择二者中更大卡方值的项，比如Robust LM-error对应的卡方值更大则使用空间误差模型，如果Robust LM-lag对应的卡方值更大则使用空间滞后模型。如果仅Robust LM-error显著则使用空间误差模型，如果仅Robust LM-lag显著则使用空间滞后模型。如果Robust LM-error和Robust LM-lag均不显著时，那么则退回去判断LM-error和LM-lag，对比LM-error和LM-lag那个对应的卡方值更大，比如LM-error对应的卡方值更大则使用空间误差模型（如果LM-lag对应的卡方值更大则使用空间滞后模型）。

这篇关于空间计量 | 空间OLS回归的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---