本文主要是介绍[BFS广度优先搜索] 迷宫,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
描述
给定一个仅由数字 0 与 1 组成的 n 行 m 列的迷宫。若你位于一格 0 上,那么你可以移动到相邻 4 格中的任意一格 1 上;同样地,若你位于一格 1 上, 那么你可以移动到相邻 4 格中的任意一格 0 上。
现在,有 q 次询问。每次询问从给定的某一格 (第 x 行,第 y 列,均从 0 开始标号) 开始,在规则内任意移动。这样,有一些格子是可能到达的,而其余格子是无法到达的。求可能到达的格子数量。
输入
输入第一行包含两个整数 n 和 m(1 ≤ n, m ≤ 103)。
接下来 n 行,每行包含 m 个 0 或 1 的整数,表示迷宫的内容。
接下来一行包含一个整数 q(0 ≤ q ≤ 105)。
接下来 q 行,每行包含两个整数 x 和 y,表示一次询问(0 ≤ x < n,0 ≤ y < m)。
输出
输出 q 行,每行一个整数,依次表示每个询问的答案。
样例输入
5 4 1 1 0 1 1 1 1 1 1 1 0 0 0 0 1 1 0 1 0 0 4 4 3 0 1 3 0 1 1
样例输出
4 11 2 1
提示
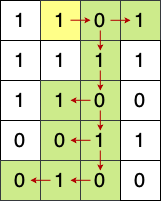
对于第二条询问,如图所示,从黄色格子 (0, 1) 出发,可分别到达所有绿色格子,包含自身共 11 格。
解题分析
这道题目首先可以看出是一道很经典的BFS广度优先搜索的题目。我们只需要用一个队列,一个visited数组,一些规则与判断就可以比较容易地去遍历我们能够到达的所有格子。但是很显然,如果我们每一个格子都这样去遍历的话,最后询问次数一旦多了起来,就很容易超时。所以我们想到了一个可以用一个数组记录下来的方法,这个时候我们还要想到其实按照题目所述的做法,我们这样是对称的。也就是说这是一个“连通块”,我们只需要找出这些连通块,每次遍历一遍后把所有走过的连通块都标记上相同的步数即可。为了更加便捷快速,我们可以用一个巧妙的自定义结构体Node创建一个数组,然后记录下我们走过的格子的位置路径,一路保存下来然后最后直接用一个循环去遍历更新即可。最后,我们的输入输出就变简单了,如果是我们已经遍历更新过的位置,那么我们直接输出路径的长度(或者说是遍历的所有格子的数量),如果是我们还没有遍历的位置,我们就调用bfs函数遍历一遍再输出我们的答案即可。
代码实现
#include <iostream>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <string>
#include <cstdio>
// #include <iomanip>
#include <map>
#include <stack>
#include <list>
#include <set>
#include <unordered_map>
#include <unordered_set>
#include <queue>
#include <sstream>
#define INF (1<<30)using namespace std;struct node{int x,y;
} f[10000100];int n,m;
char maze[1001][1001]={0};
int record[1001][1001]={0};
bool visited[1001][1001]={0};
int dx[]={0,0,1,-1};
int dy[]={1,-1,0,0};void bfs(int x,int y){queue<node> q;q.push({x,y});visited[x][y]=1;node tmp;int t=0;while(!q.empty()){tmp=q.front();q.pop();if(record[tmp.x][tmp.y]) continue;for(int i=0;i<4;i++){int nx = tmp.x + dx[i] , ny = tmp.y + dy[i];if(nx <= 0 || ny <= 0 || nx > n || ny > n) continue;if(visited[nx][ny] || record[nx][ny]) continue;if(maze[nx][ny]==maze[tmp.x][tmp.y]) continue;q.push({nx,ny});visited[nx][ny]=1;f[t].x=nx; f[t].y=ny;t++;}}record[x][y]=t+1;for(int i=0;i<t;i++){record[f[i].x][f[i].y]=t+1;}
}int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){scanf("%s",maze[i]+1);}int tmpx,tmpy;for(int i=0;i<m;i++){scanf("%d%d",&tmpx,&tmpy);if(record[tmpx][tmpy]) printf("%d\n",record[tmpx][tmpy]);else {bfs(tmpx,tmpy);printf("%d\n",record[tmpx][tmpy]);}}return 0;
}这篇关于[BFS广度优先搜索] 迷宫的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



