电影数据集关联分析及FP-Growth实现

本文主要是介绍电影数据集关联分析及FP-Growth实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

（1）数据预处理

我们先对数据集进行观察，其属性为’movieId’ ‘title’ ‘genres’，其中’movieId’为电影的序号，但并不完整，‘title’为电影名称及年份，‘genres’为电影的分类标签。因此电影的分类标签可以作为我们研究此数据集关联分析的文本数据。

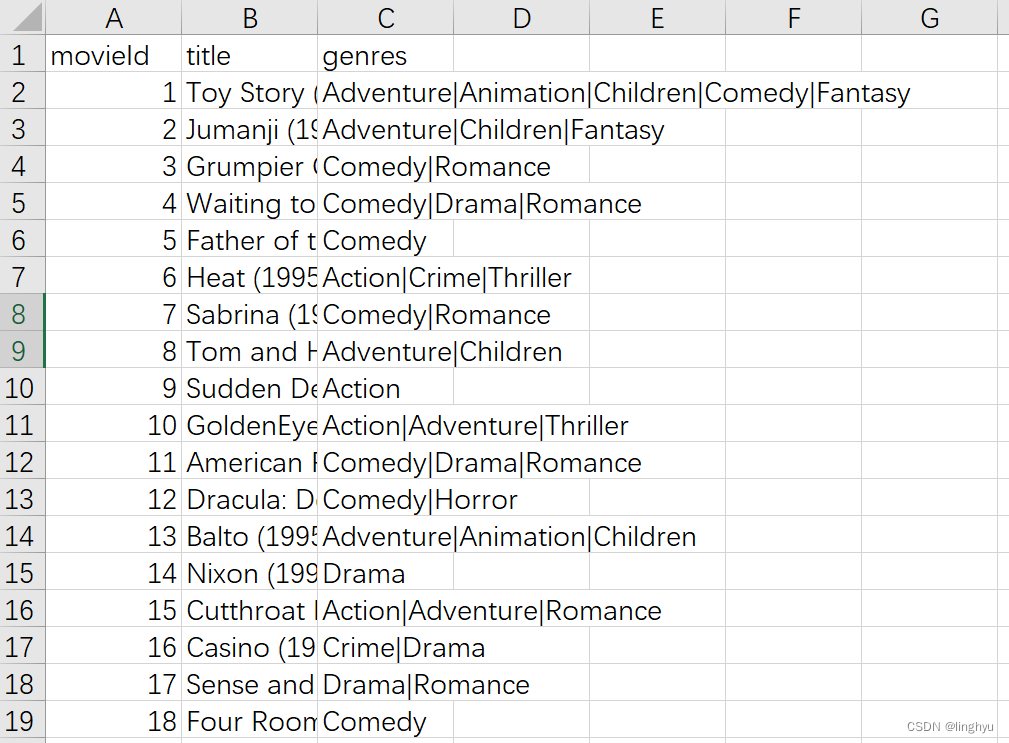
我们可以看到电影的分类标签在同一个电影下不只有一个，且用’|’分开，因此我们对数据进行以下处理：

import pandas as pd
import csv
with open("movies.csv", mode="r", encoding='gb18030', errors='ignore') as file:csv_reader = csv.reader(file)next(csv_reader) # 跳过表头li = []for row in csv_reader:li.append(row[2].split("|"))

导入必要库，读取csv第三列去表头的文件数据，并且进行文本分割，将分割完的数据存储进列表里，作为后面算法进行关联分析的数据集。下图是处理完的数据集部分数据：

（2）代码

import pandas as pd # 导入必要库
import csv
from itertools import combinationsli = []
k = 0
with open("movies.csv", mode="r", encoding='gb18030', errors='ignore') as file:csv_reader = csv.reader(file)next(csv_reader) # 跳过表头for row in csv_reader:li.append(row[2].split("|")) # 处理第三列数据# print(li)
# 设置最小支持度和最小置信度阈值
min_support = 0.05
min_confidence = 0.5
# 统计每个项的支持度
item_support = {}
for transaction in li:for item in transaction:if item not in item_support:item_support[item] = 0item_support[item] += 1
# 计算总事务数
total_transactions = len(li)
# print(item_support)
# 计算频繁项集
frequent_itemsets = {}
for item, support in item_support.items():if support / total_transactions >= min_support: # 即该项集在事务数据库中出现frequent_itemsets[(item,)] = support / total_transactions
# 生成候选项集并迭代生成频繁项集
k = 2
while True:candidates = set() # 存储所有可能的项集for itemset in frequent_itemsets.keys():for item in itemset:candidates.add(item)# 生成候选项集candidates = list(combinations(candidates, k)) # 生成所有可能的k项集# 统计候选项集的支持度candidate_support = {}for transaction in li:for candidate in candidates:if set(candidate).issubset(set(transaction)):if candidate not in candidate_support:candidate_support[candidate] = 0candidate_support[candidate] += 1# 更新频繁项集frequent_itemsets_k = {}for candidate, support in candidate_support.items():if support / total_transactions >= min_support:frequent_itemsets_k[candidate] = support / total_transactions# 如果没有频繁项集则停止迭代if not frequent_itemsets_k:breakfrequent_itemsets.update(frequent_itemsets_k)k += 1
# print(frequent_itemsets)
# 生成关联规则
rules = []
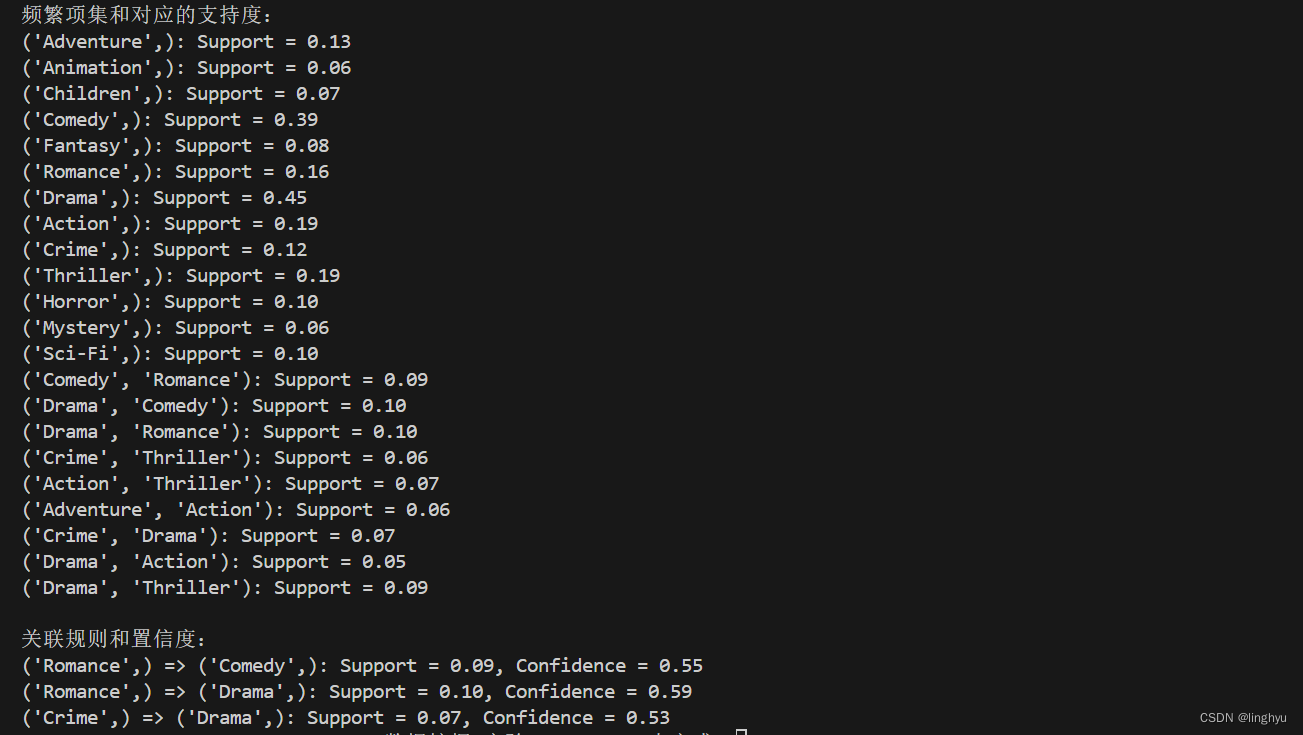
for itemset in frequent_itemsets.keys():if len(itemset) >= 2:for i in range(1, len(itemset)):for combination in combinations(itemset, i):X = combinationY = tuple(set(itemset) - set(combination))confidence = frequent_itemsets[itemset] / frequent_itemsets[X]if confidence >= min_confidence:rules.append((X, Y, frequent_itemsets[itemset], confidence))# return frequent_itemsets, rulesprint("频繁项集和对应的支持度：")
for itemset, support in frequent_itemsets.items():print("{}: Support = {:.2f}".format(itemset, support))
# 输出关联规则和置信度
print("\n关联规则和置信度：")
for X, Y, support, confidence in rules:print("{} => {}: Support = {:.2f}, Confidence = {:.2f}".format(X, Y, support, confidence))

（3）输出结果截图

（4） FP-Growth

import pandas as pd # 导入必要库
import csv
from itertools import combinationsli = []
k = 0
with open("movies.csv", mode="r", encoding='gb18030', errors='ignore') as file:csv_reader = csv.reader(file)next(csv_reader) # 跳过表头for row in csv_reader:li.append(row[2].split("|")) # 处理第三列数据# print(li)
# 设置最小支持度和最小置信度阈值
min_support = 0.05
min_confidence = 0.5
# 统计每个项的支持度
item_support = {}
for transaction in li:for item in transaction:if item not in item_support:item_support[item] = 0item_support[item] += 1
# 计算总事务数
total_transactions = len(li)
# print(item_support)
# 计算频繁项集
frequent_itemsets = {}
for item, support in item_support.items():if support / total_transactions >= min_support: # 即该项集在事务数据库中出现frequent_itemsets[(item,)] = support / total_transactions
# 生成候选项集并迭代生成频繁项集
k = 2
while True:candidates = set() # 存储所有可能的项集for itemset in frequent_itemsets.keys():for item in itemset:candidates.add(item)# 生成候选项集candidates = list(combinations(candidates, k)) # 生成所有可能的k项集# 统计候选项集的支持度candidate_support = {}for transaction in li:for candidate in candidates:if set(candidate).issubset(set(transaction)):if candidate not in candidate_support:candidate_support[candidate] = 0candidate_support[candidate] += 1# 更新频繁项集frequent_itemsets_k = {}for candidate, support in candidate_support.items():if support / total_transactions >= min_support:frequent_itemsets_k[candidate] = support / total_transactions# 如果没有频繁项集则停止迭代if not frequent_itemsets_k:breakfrequent_itemsets.update(frequent_itemsets_k)k += 1
# print(frequent_itemsets)
# 生成关联规则
rules = []
for itemset in frequent_itemsets.keys():if len(itemset) >= 2:for i in range(1, len(itemset)):for combination in combinations(itemset, i):X = combinationY = tuple(set(itemset) - set(combination))confidence = frequent_itemsets[itemset] / frequent_itemsets[X]if confidence >= min_confidence:rules.append((X, Y, frequent_itemsets[itemset], confidence))# return frequent_itemsets, rulesprint("频繁项集和对应的支持度：")
for itemset, support in frequent_itemsets.items():print("{}: Support = {:.2f}".format(itemset, support))
# 输出关联规则和置信度
print("\n关联规则和置信度：")
for X, Y, support, confidence in rules:print("{} => {}: Support = {:.2f}, Confidence = {:.2f}".format(X, Y, support, confidence))