本文主要是介绍算法与数据结构 | 时间复杂度分析 / 更准确的描述代码的时间复杂度,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 数据结构与算法概述
- 复杂度分析
- 大O复杂度表示法
- 时间复杂度分析
- 几种常见时间复杂度实例分析
- 空间复杂度分析
- 复杂度坐标图
- 复杂度分析的四个知识点
数据结构与算法概述
- 什么是数据结构?什么是算法?
- 从广义上讲,数据结构就是指一组数据的存储结构。算法就是操作数据的一组方法。
- 从狭义上讲,是指某些著名的数据结构和算法,比如队列、栈、堆、二分查找、动态规划等。
- 算法和数据结构直接的关系
- 数据结构是为算法服务的,算法要作用在特定的数据结构之上。
- 复杂度分析–算法中重要的概念
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树;
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法。
复杂度分析
大O复杂度表示法
- 求1,2,3…n 累加的和,代码如下:
int cal(int n) {int sum = 0;int i = 1;for (; i <= n; ++i) {sum = sum + i;}return sum;}- 计算机执行的操作是:读数据-运算-写数据
- 假设
int sum = 0;级别的一行代码需要一个Time,则以上的for循环则需要2n* Time;整个代码执行时间就是T(n)=2* Time+2n * Time;提取公因式变成T(n)=(2+2n)* Time;,则表示每行代码的执行时间和总时间成正比; - 抽象公式,把每一行代码的执行时间抽象为大O,公式则可以抽象为
T(n)=O*f(n);这就是大 O 时间复杂度表示法; - 大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度(asymptotic time complexity),简称时间复杂度。
时间复杂度分析
- 如何分析一段代码的时间复杂度?
- 只关注循环执行次数最多的一段代码
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
几种常见时间复杂度实例分析

多项式量级和非多项式量级- O(1)
- 常量时间复杂度
- 一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)。
- O(logn)、O(nlogn)
- O(m+n)、O(m* n)
空间复杂度分析
- 表示算法的存储空间与数据规模之间的增长关系。
复杂度坐标图
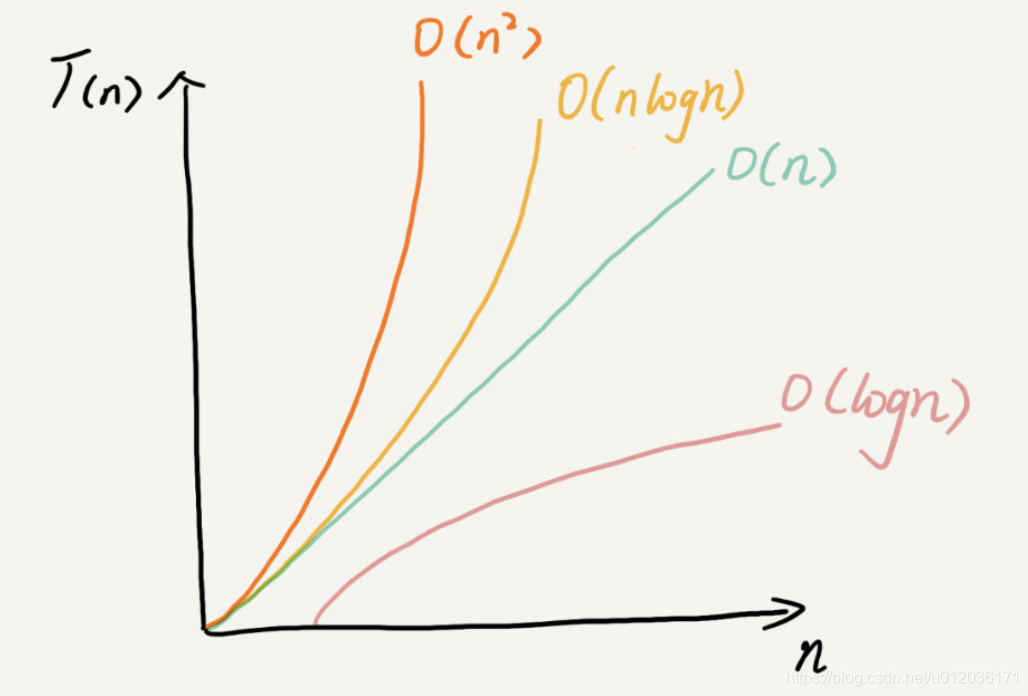
复杂度分析的四个知识点
- 最好情况时间复杂度
- 一个for循环,在满足条件的时候break;跳出循环
- 最坏情况时间复杂度
- for循环循环完
- 平均情况时间复杂度
- 用代码在所有情况下执行的次数的加权平均值表示
- 均摊时间复杂度
- 在代码执行的所有复杂度情况中绝大部分是低级别的复杂度,个别情况是高级别复杂度且发生具有时序关系时,可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。
这篇关于算法与数据结构 | 时间复杂度分析 / 更准确的描述代码的时间复杂度的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






