采用calyer画多边形

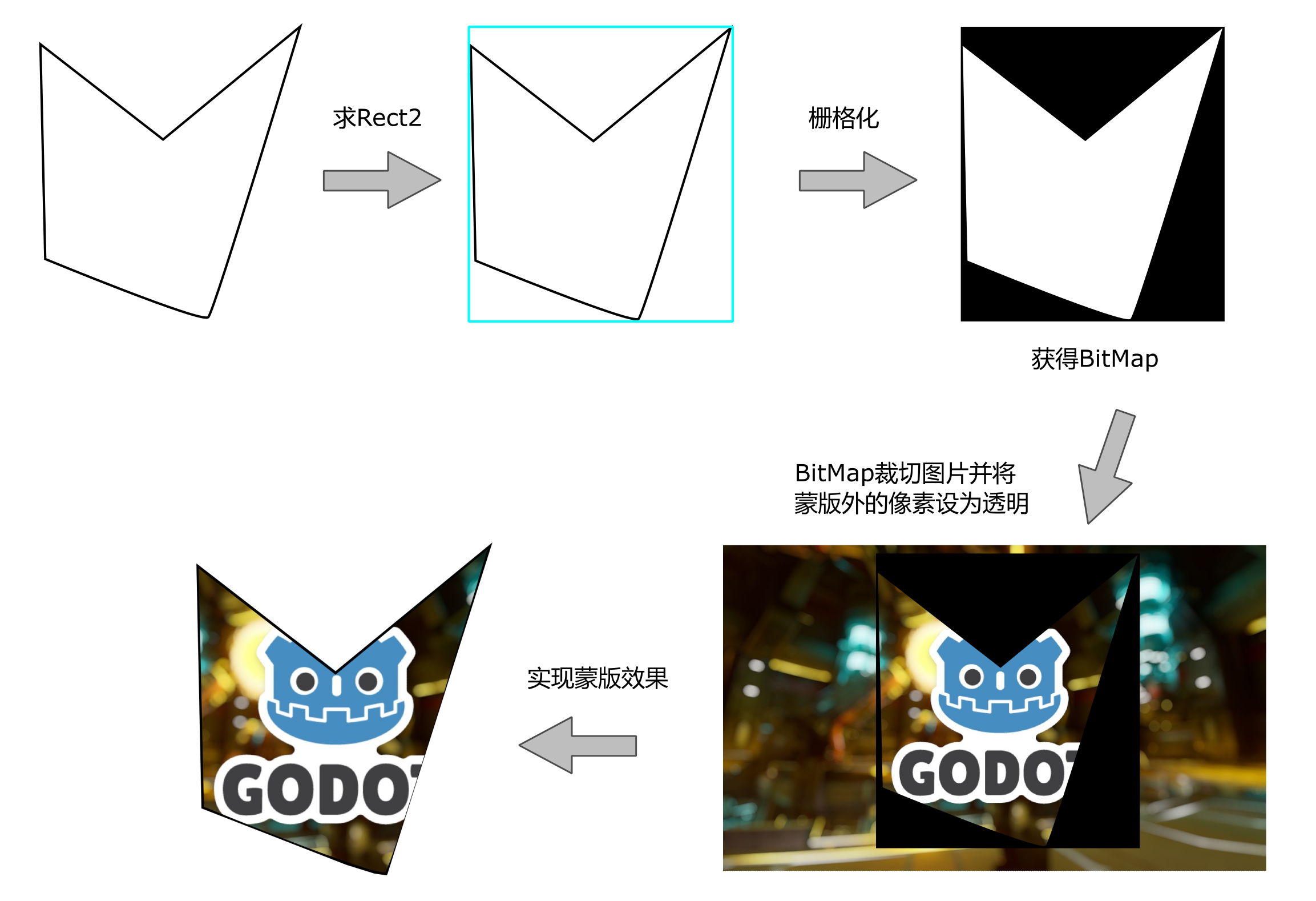
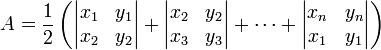本文主要是介绍采用calyer画多边形，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一直想用calyer做点什么东西，昨天有空探究了下calyer这个东西，如果做动画在calyer层上需要增加新的layer跟uiview addsubview有点类似。但是动画的显示还是有不同之处的。下面上代码显示的结果是一个正五边形
//绘画一个多边形(五边形)
CGFloat x0 = 160.0f;
CGFloat y0 = 200.0f;
CGFloat x ;
CGFloat y ;
CGFloat radius = 150.0f;
UIBezierPath *movePath = [UIBezierPath bezierPath];
CGFloat huDuFromdu = M_PI/(180/72.0);
for (NSInteger i=0; i<6; i++) {
//cos在ios中不能直接用需要cosf转换的弧度中间转换下
x = x0 + radius * cosf(i*M_PI/(180/du));
y = y0 - radius * sinf(i*M_PI/(180/du));
if (i==0) {
[movePath moveToPoint:CGPointMake(x, y)];
}
else
{
[movePath addLineToPoint:CGPointMake(x, y)];
}
}
[movePath closePath];

//添加渲染
CAShapeLayer *oneLayer = [CAShapeLayer layer];
oneLayer.fillColor = [UIColor yellowColor].CGColor;
oneLayer.path = movePath.CGPath;
oneLayer.strokeColor = [UIColor orangeColor].CGColor;
oneLayer.lineWidth=2;
[self.view.layer addSublayer:oneLayer];

这篇关于采用calyer画多边形的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---