本文主要是介绍什么是 古典概型,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
古典概型是概率论中的一种基本概型,其定义如下:
古典概型(Classical Probability Model):
在一个有限的样本空间中,如果每个基本事件(即样本空间中的每一个可能结果)出现的可能性都是相同的,那么这种概率模型称为古典概型。
特点
- 有限性:样本空间中的所有可能结果是有限个。
- 等可能性:样本空间中的每一个基本事件发生的概率是相同的。
计算方法
在古典概型中,事件 A 发生的概率 P(A) 可以通过以下公式计算:
P ( A ) = ∣ A ∣ ∣ S ∣ P(A) = \frac{|A|}{|S|} P(A)=∣S∣∣A∣
其中:
- |A| 表示事件 A 所包含的基本事件的个数。
- |S| 表示样本空间 S 中基本事件的总数。
例子
- 掷骰子:一个标准的六面骰子,每一面出现的概率都是相等的,即 1 6 \frac{1}{6} 61。假设事件 A 是掷出一个偶数,那么 A 包含 {2, 4, 6} 三个基本事件。所以 P ( A ) = 3 6 = 1 2 P(A) = \frac{3}{6} = \frac{1}{2} P(A)=63=21。
- 抛硬币:一个标准的硬币,有两个面:正面和反面。每一面出现的概率都是 1 2 \frac{1}{2} 21。假设事件 B 是抛出正面,那么 P ( B ) = 1 2 P(B) = \frac{1}{2} P(B)=21。
应用
古典概型适用于那些所有可能结果都已知且等可能的情况,如掷骰子、抛硬币、从一副完整的扑克牌中抽牌等。
通过这种模型,可以简单直观地计算事件发生的概率,并且在许多实际问题中都有广泛应用。
这篇关于什么是 古典概型的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





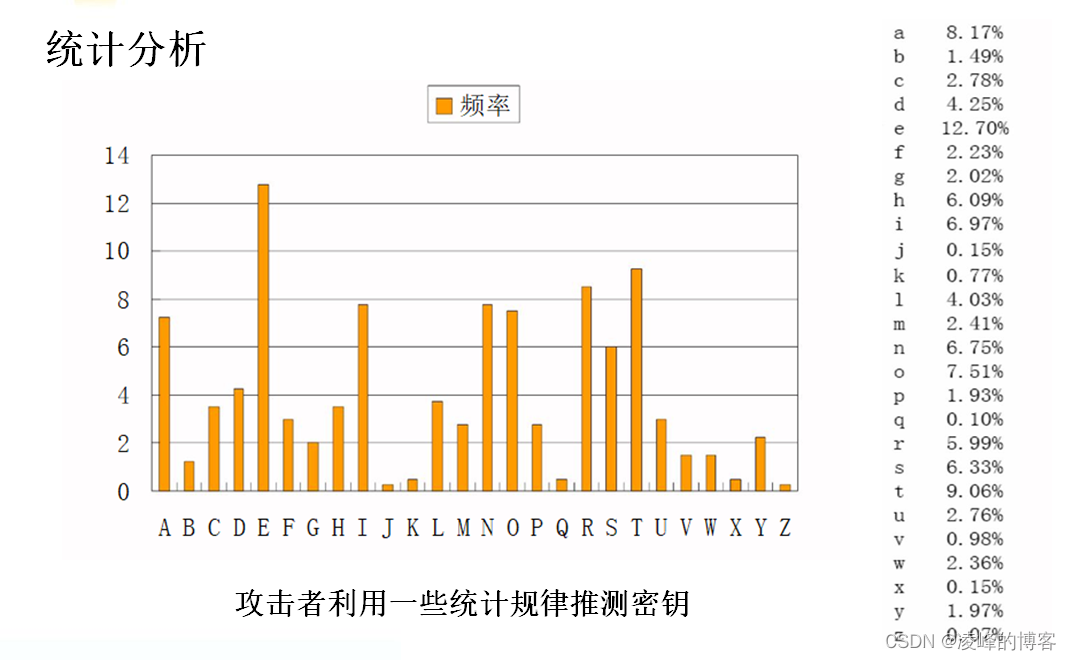
![[BJDCTF 2020]base??(古典密码)](https://img-blog.csdnimg.cn/direct/66178e15508c41d59b5c10beceaf1403.png)
