本文主要是介绍Cvbox2D 角度 长宽正解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文档转自:https://www.cnblogs.com/panxiaochun/p/5478555.html
cvBox2D和RotatedRect中返回的角度angle详解
本文为作者原创,未经允许不得转载;
原文由作者发表在博客园: http://www.cnblogs.com/panxiaochun/p/5478555.html
关于cvBox2D和RotatedRect中返回的角度angle的opencv官方说明文档里面没有给出太多到信息,其中文档是这样说的:

图1:opencv关于cvBox2D的说明文档截图
在水平轴和第一条边之间的角度。(好简洁,但是真的并没有太明确)
在网上也有关于cvBox2D和RotatedRect的角度angle的说明,但是查看了一下,不对,或者不完全对。其中有两篇:http://blog.csdn.net/mine1024/article/details/6044856和
http://blog.csdn.net/a553654745/article/details/45743063,其中说到了,x轴逆时针碰到的第一条边为width(实际中width可能比Height还大,实际使用中确实发现了width比height还大的情况),下面选取两篇文章中的图来说明一下:
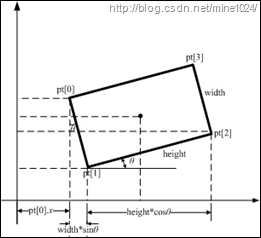
图2:网友关于旋转角的说明图
这幅图是网上流传最多的,但是只有一篇原创,其它都是复制粘贴,有的甚至只是放了一幅图,这篇博文只告诉我们一个有用的东西,x轴逆时针碰到的第一条边为width,并与这条边形成的角度就是cvBox2D和RotatedRect的角度angle,但是这篇博文忽略了,一个事实就是opencv的坐标原点是左上角,所以这个坐标系是错的。下面的图就比较完整的说明了cvBox2D和RotatedRect的角度的来源:
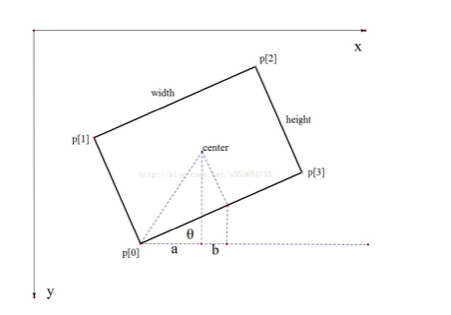
图3:网友关于opencv旋转角的修正图
这个图是很好说明角度的选取的来源,但是我本人觉得有点错误所以,修正了一下:
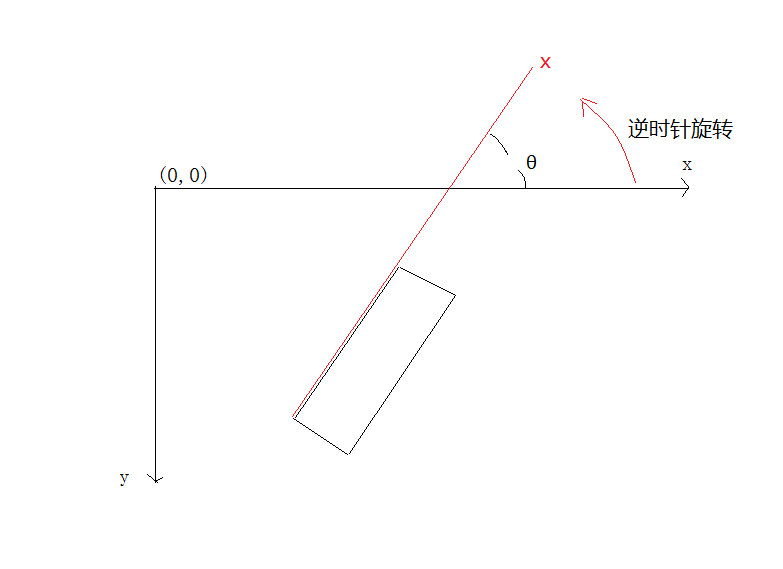
图4:我个人关于cvBox2D和RotatedRect里面的角度angle的说明图
这是本人修改过的图,下面进入论证,这里用了一幅图,里面有两个旋转的矩形,其中由于旋转的角度不一样,所以opencv找出来的cvBox2D里面的width有可能会比height大

图5:测试图片里面的两个矩形图
其中第一个由于它是逆时针旋转的,所以,x轴会先碰到顶部的直线L1,第二个矩形是顺时针旋转的,所以x轴会先碰到左边的直线L2,很明显L2会比L1大,其中L1也会比它左边的直线小:

图6:第一个矩形的检测结果图
第一个矩形的角度只有-22度(再次证明不是书上说的弧度)其中width为130,比height小。

图7:第二个矩形的检测结果图
第二个矩形的角度为-77度,width为234,比height109大,其中还比第一个矩形的width大。论证成立。
其中角度的正负,在网上很多都说逆时针为正,顺时为负,这里逆时针为负,顺时针为正,主要原因,我个人觉得是和坐标系有关,因为网上说的角度的旋转的坐标系是以图2的坐标系作为参考,而opencv里面是以图3的作为参考,所以在x轴和y轴的象限里的角度为正的原则吧,opencv里逆时针为负。
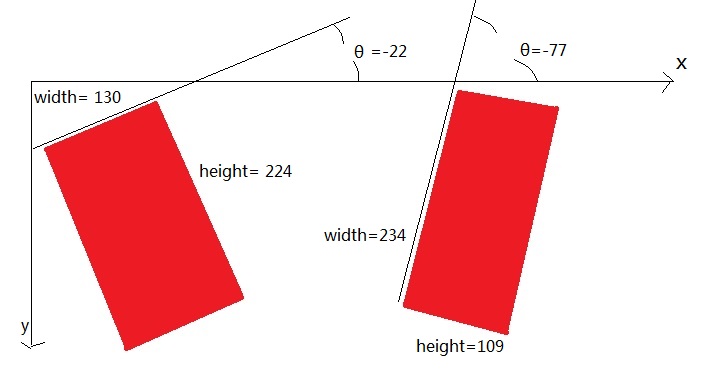
图8:论证结果详解图
在opencv的源码的\modules\ imgproc\src下的rot calipers.cpp里可以找到minareaRect()函数的源码,该函数会返回RotatedRect,在c#版会返回CvBox2D,两个是一样的,在里面找到了angle不是弧度最佳证明:
box.angle = (float)(box.angle*180/CV_PI);
可以看出返回的RotatedRect的angle不是弧度单位,刚开始angle是弧度的,后来经过转换后再输出了,可能前几个版本里面的angle是弧度的后来改为度了。
https://www.vsien.cn/
这篇关于Cvbox2D 角度 长宽正解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






