【自动驾驶】27.相机畸变_相机内参标定 整理

本文主要是介绍【自动驾驶】27.相机畸变_相机内参标定 整理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

这篇文章讲解的很详细，包括在哪一步添加畸变：【自动驾驶视觉感知：相机标定】

本文整理了很多有关相机畸变博客的相关内容，都附上的原文地址，也纠正了一些其他博客的错误。

---

下面两张截图来自高翔博士的《视觉SLAM十四讲》书中内容。

有关添加畸变矫正以及去畸变的详细过程，可以参考 自动驾驶视觉感知：相机标定。

关于相机内参标定的请参考这篇博客：最详细、最完整的相机标定讲解。 注意，这篇博客的畸变矫正公式也写反了。

相机畸变公式推导可参考这篇博客：相机畸变详细推导。

【畸变矫正公式参数说明：】
网上有很多文章都在谈畸变矫正，对于畸变矫正的公式，有很多文章是把畸变前的像素坐标和畸变后的像素坐标的关系搞反了，下面给出正确的关系：

引用张正友论文的原文：
《Flexible camera calibration by viewing a plane from unknown orientations》

由上述论文可见， 畸变公式左侧 $\breve{x}$ 、$\breve{y}$ 是畸变矫正前的像素坐标，右侧的 $x$ 、$y$ 是理想情况下无畸变时的像素坐标：
正确公式如下：
径向畸变：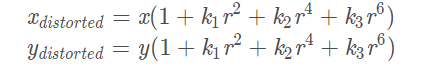

切向畸变：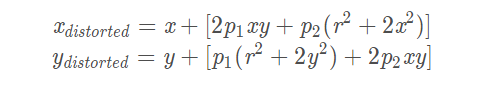

网上有些博客搞反了， 他们说等式左侧 是畸变矫正后的结果。

这里只是关于畸变公式中参数的意义做了一个说明记录，关于畸变的矫正的代码及详细原理解释可参考下面这个博客，写的很好：https://www.jianshu.com/p/6daa8dbbfa30

---

原文链接：https://blog.csdn.net/TimeRiverForever/article/details/117283430

透镜

实际成像时，如果小孔过小，则入射光的强度会受到影响，进一步会影响到成像。 另一方面，由于光的波动性，在小孔的边缘上，光将发生衍射，因此，这些光将在像平面上“散播”。当小孔变的越来越小时，入射光的“散播”范围将变得越来越大，因此，入射光中越来越多的能量将会被“散播”到：偏离入射光方向的“地方”。

我们在使用针孔相机时，我们做过一个假设：针孔是无线小的一个孔。在真实物理世界中，我们的假设一般无法成立，那如果改变针孔的大小后，会发生怎样的变化呢？

如上图所示，当针孔尺寸发生改变后，穿过针孔的光线数量就会增加。光线数越多，像平面中的点就会被三维世界中物体上越多的点影响，导致图像越发模糊。针孔小了，得到的图像更清晰，但也更暗。自然而然的，我们就会想到针孔模型下的一个基本问题：我们能设计一个相机能得到既清晰又明亮的图像吗？

为了解决小孔相机的上述问题，我们现在考虑：在成像系统中使用透镜。镜头可以使光线聚焦或分散，如果我们选用一个理想的透镜替代针孔，那他应该具有以下特性：P点发出的所有射线，经镜头折射后，聚焦在像平面上P′点。

假如我们另取一点 Q，在像平面上的投影点则可能是模糊或失焦的。每个镜头都会有特定的准确对焦的距离，在摄影学或计算机图形学中也叫景深（depth of field）。

镜头能够讲所有平行于光轴的光线折射到同一个点，称之为焦点。焦点和光心的距离即为焦距f。从光心穿过的光线不会偏离原始方向。
一个理想的透镜具有如下两个性质：

• 它的投影方式和小孔模型相同
• 将一定数量的光线汇聚在一起。

畸变模型参数

相机的内参除了以上f_x, f_y, u₀, v₀，还包含畸变系数[k₁, k₂, p₁, p₂, k₃]
理想的透镜是没有畸变的。但是，因为制造和安装精度等方面的原因，镜头总是存在这畸变。畸变是相机固有特性，同款相机的畸变也会有些许差异，但是其和相机内参一样，标定一次即可。

畸变参数分为径向畸变（Radial Distortion）和切向畸变（Tangential Distortion），除了这两种之外也还有其他类型畸变，但是没有这两种显著，故忽略不计。

径向畸变

径向畸变来自透镜形状不规则以及建模的方式，导致镜头不同部分焦距不同。光线在远离透镜中心的地方偏折更大（枕型畸变）或更小（桶形畸变）。

从径向畸变开始。实际摄像机的透镜总是在成像仪的边缘产生显著的畸变，如下图所示。对某些透镜，光线在远离透镜中心的地方比靠近中心的地方更加弯曲。

对径向畸变，成像仪中心（光轴）的畸变为0，随着向边缘移动，畸变越来越严重。当然，在实际的相机中，这种畸变比较小，而且可以用r=0位置周围的泰勒级数展开的前几项来定量描述。

等号左边是畸变，右边的x，y是理想值。

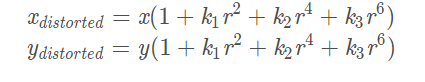
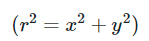
下图显示矩形网格因径向畸变而产生的位移。越远离光轴中心的地方，矩形网格上的点偏移越大。

下图描述了3种常见的畸变情形，桶形畸变通常k1>0，枕形畸变通常k1<0。

切向畸变

切向畸变来自于整个摄像机的组装过程。由于透镜制造上的缺陷使得透镜本身与图像平面不平行而产生的，如下图所示：

切向畸变可以用两个额外的参数p₁和p₂来描述：

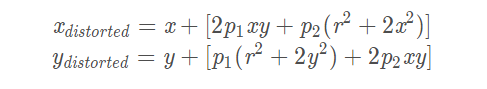
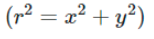
去畸变计算

到目前位置，相机的模型已经建立起来了，以下公式中的矩阵描述了相机的固有参数

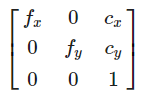
有时(u₀, v₀)也写作(c_x, c_y)，以及畸变参数：Distortion_coefficients=(k₁，k₂，p₁，p₂，k₃)

决定这两个矩阵的过程，便是相机标定。通常，把摄像机对准一个有很多独立可标识点的物体，在不同角度观看这个物体，进一步可通过每个图像来计算摄像机的相对位置和方向，以及摄像机的内参。

在内参标定完成后，可以建立三维坐标和二维图像的关系：

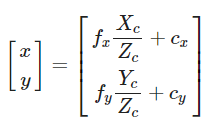
综合径向畸变和切向畸变，我们总结出去畸变公式：

• Ideal point (x_u,y_u)为理想点
• real point (x_d,y_d)为实际点
• dr为径向畸变，参数为{k₁, k₂, k₃}
• dt为切向畸变，参数为{p₁, p₂}
  于是通过下面的变换，可以得到没有畸变的标定结果：
  

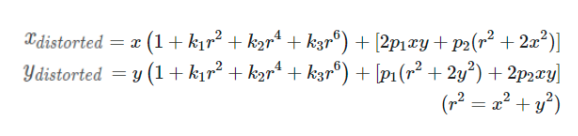
等式右边的(x, y)为得到的图像中的理想点，但是存在畸变，于是把其带入等式左边，经过径向和切向变换后，得到右边的畸变校正后的实际点坐标(x_corrected, y_corrected)，取出对应颜色值作为(x, y)的颜色值即可。通过去畸变，可以完成图像的矫正，如下图：

注：以上文字和图片均来源于链接，若有侵权请联系转载方删除。

这篇关于【自动驾驶】27.相机畸变_相机内参标定 整理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---